偏差方差权衡(bias variance trade off)
偏差:如果说一个模型欠拟合,也可以说它的偏差很大。
方差:如果说一个模型过拟合,也可以说它的方差很大。
训练误差
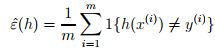
经验风险最小化(ERM)
选择参数,使得训练误差最小化,即
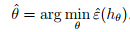
假设类H:所有假设构成的集合。
ERM的目标也可以写成选择假设,使得训练误差最小化,即
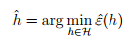
泛化误差(generalization error)
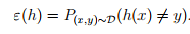 ,即对于新样本错误分类的概率。
,即对于新样本错误分类的概率。
联合界引理(the union bound)
事件和的概率小于等于事件概率之和。
Hoeffding不等式引理
令z1,...,zm为i,i,d,并且服从伯努利分布,即P(zi=1)=phi,P(zi=0)=1-phi。定义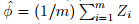 ,对于给定的gamma,Hoeffding不等式为,
,对于给定的gamma,Hoeffding不等式为,
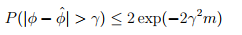
ERM的性质
以有限假设类为例
令H为一个包含了k个假设的假设类。这k个函数都是从输入映射到输出的函数,不带有参数。ERM需要做的就是,对于给定的训练集合,从假设类中找到一个假设,使得训练误差最小。我们更喜欢的是泛化误差较小。所以,先证明训练误差是泛化误差的近似,然后可以证明ERM输出的泛化误差具有上界。以下为证明过程
对于假设类里面的某一个特定假设hi,定义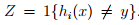 ,那么训练误差即为
,那么训练误差即为
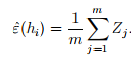 ,则训练误差为泛化误差的平均数,则有
,则训练误差为泛化误差的平均数,则有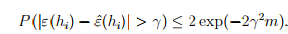 所以对于某一个假设来说,训练误差和泛化误差是近似的。令Ai=
所以对于某一个假设来说,训练误差和泛化误差是近似的。令Ai=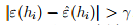 ,则
,则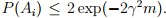 。
。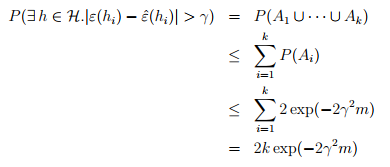
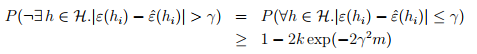 。所以,对于所有的假设,训练误差和泛化误差是近似的,即一致收敛。
。所以,对于所有的假设,训练误差和泛化误差是近似的,即一致收敛。
对于给定的gamma与delta,令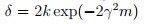 ,则可以确定样本的数量m,
,则可以确定样本的数量m,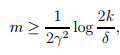 ,这也叫样本复杂度。
,这也叫样本复杂度。
对于给定的m与delta,可以求解出gamma。在1-delta的概率下,有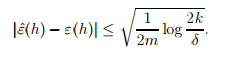 ,所以不等式右边的即为gamma。
,所以不等式右边的即为gamma。
定义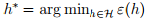 ,同时
,同时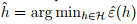 。则,
。则,
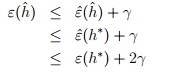
定理:令假设类是一个k个假设的集合,令m和delta固定,在至少1-gamma的概率下,有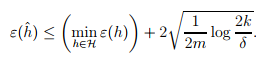 第一项对应着算法的偏差,第二项对应着假设的方差。通过使用一个更为复杂的假设类,会使得方差变大,偏差变小。
第一项对应着算法的偏差,第二项对应着假设的方差。通过使用一个更为复杂的假设类,会使得方差变大,偏差变小。