树链剖分
对于一棵树上两个节点所构成的链的操作,我们可以用树链剖分,来将树转化为多条链的集合(线性结构),从而将树上链的结构转化为线性结构的区间操作.
- 找出每个节点的重儿子(包含节点最多的儿子)
- 重儿子优先输出dfs序
对于如下一棵树进行剖分
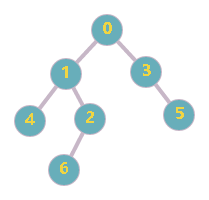
找出其重儿子(红色线)
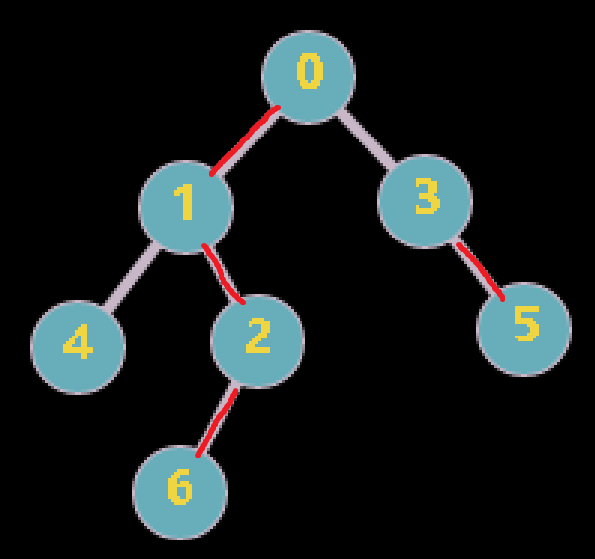
每个节点与其重儿子递归组成一条链(叶子节点没有重儿子)
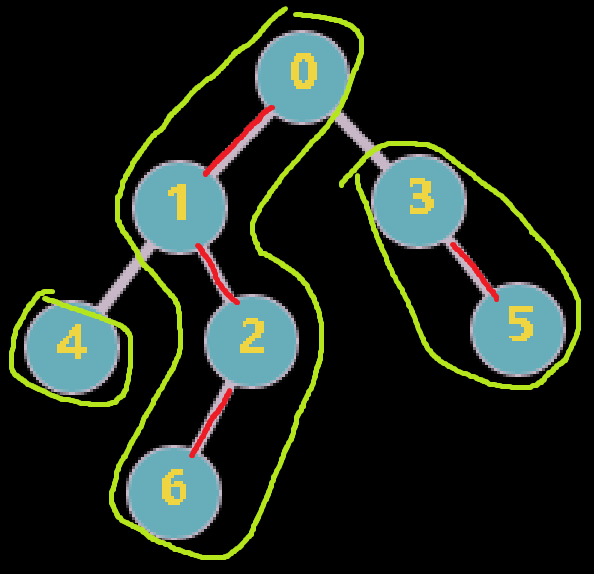
树链剖分后的序列为: (0,1,2,6,3,5,4)
现在要修改两个点路径上所有点的权值,假如两个点在一条链上,就直接修改序列的区间.否则就修改从当前点到链根的区间,然后跳到链根的父亲递归修改.
比如现在要修改(4到5)的所有点的权值
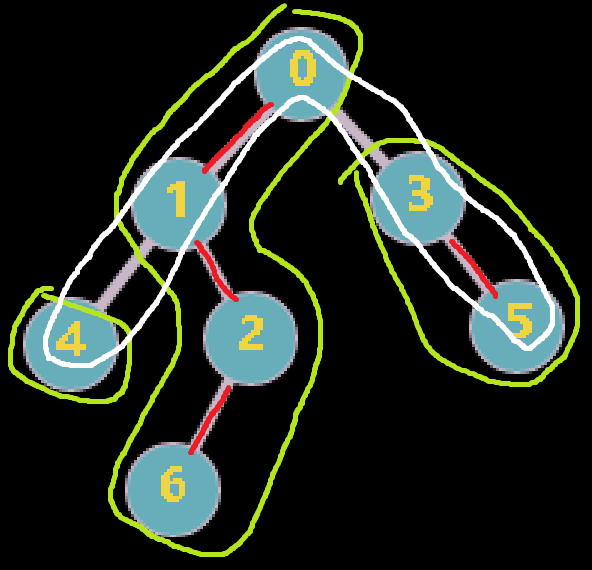
- 4所在的链根为4,所以修改4到4,然后跳到4的父亲1
- 5所在的链根为3,所以修改3到5,然后跳到3的父亲0
- 1,0在同一条链上,直接修改1到0
所以对于树链剖分序的区间修改(dfs序的下标)为: 7-7,5-6,1-2
BZOJ 1036
- 题意: 树上查询区间最大值,区间和,单点修改
- 思路(
好吧直接抄的代码): 先树链剖分,利用线段树维护信息和询问
#include<bits/stdc++.h>
#define ll long long
#define FOR(i,l,r) for(int i = l ; i <= r ;++i )
#define inf 0x3f3f3f3f
#define EPS (1e-9)
#define ALL(T) T.begin(),T.end()
#define lson(i) i<<1
#define rson(i) (i<<1|1)
using namespace std;
const int maxn =30010;
struct Edge{
int to,next;
}edge[maxn*2];
int head[maxn],tot; //前向星
int top[maxn]; // 所在重链的顶端节点
int fa[maxn]; // 父亲
int deep[maxn]; // 深度
int num[maxn]; // 子节点个数
int p[maxn]; // 在dfs序的位置
int fp[maxn]; // 位置节点号的反向映射
int son[maxn]; // 重儿子
int pos; // dfs序当前下标
// 加边
void addedge(int u,int v){
edge[tot].to = v;
edge[tot].next = head[u];
head[u] = tot++;
}
// 初始化
void init(){
memset(head,-1,sizeof(head));
memset(son,-1,sizeof(son));
tot = 0;
pos = 1;
}
//第一遍dfs 处理fa,num,deep,son
void dfs1(int u,int pre,int d){
deep[u] = d;
fa[u] = pre;
num[u] = 1;
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].to;
if(v!=pre){ // 所指边不是父亲
dfs1(v,u,d+1);
num[u] += num[v]; // 更新父亲子节点数量
if(son[u] == -1 || num[v] > num[son[u]])
son[u] = v; // 更新父亲重儿子
}
}
}
// 第二遍dfs 处理 top,p,fp
void dfs2(int u,int sp){
top[u] = sp;
p[u] = pos++;
fp[p[u]] = u;
if(son[u]== -1) return ;
dfs2(son[u],sp); // 当前链继续走重儿子
for(int i=head[u];i!=-1;i=edge[i].next){
int v = edge[i].to;
if( v!= son[u] && v!=fa[u])
dfs2(v,v); // 以自己为链首的新链
}
}
// 原数组
int a[maxn];
struct node{
int l,r;
int sum,ma;
}seg[maxn*4];
// 线段树操作
void push_up(int p){
seg[p].sum = seg[lson(p)].sum + seg[rson(p)].sum;
seg[p].ma = max(seg[lson(p)].ma,seg[rson(p)].ma);
}
void build(int pp,int l,int r){
seg[pp].l = l;
seg[pp].r = r;
if(l==r){
// 这里要注意反向映射回原数组下标
seg[pp].ma = seg[pp].sum = a[fp[l]];
return;
}
int mid = (l+r)>>1;
build(lson(pp),l,mid);
build(rson(pp),mid+1,r);
push_up(pp);
}
void update(int p,int l,int r,int val){
if(seg[p].l >= l && seg[p].r <= r){
seg[p].sum = val;
seg[p].ma = val;
return;
}
int mid = (seg[p].r+seg[p].l)>>1;
if(l<=mid) update(lson(p),l,r,val);
if(r>mid) update(rson(p),l,r,val);
push_up(p);
}
int qmax(int p,int l,int r){
if(seg[p].l >= l && seg[p].r <= r){
return seg[p].ma;
}
int res = -inf;
int mid = (seg[p].r+seg[p].l)>>1;
if(l<=mid) res = max(res,qmax(lson(p),l,r));
if(r>mid) res = max(res,qmax(rson(p),l,r));
return res;
}
int qsum(int p,int l,int r){
if(seg[p].l >= l && seg[p].r <= r){
return seg[p].sum;
}
int res = 0;
int mid = (seg[p].r+seg[p].l)>>1;
if(l<=mid) res = res+qsum(lson(p),l,r);
if(r>mid) res = res+qsum(rson(p),l,r);
return res;
}
// 查询和
int fsum(int u,int v){
int res = 0;
int tu = top[u], tv = top[v];
while(tu != tv){
if(deep[tu]< deep[tv]){
swap(tu,tv);
swap(u,v);
}
res+= qsum(1,p[tu],p[u]);
u = fa[tu];
tu = top[u];
}
if(deep[u] > deep[v]) swap(u,v);
res += qsum(1,p[u],p[v]);
return res;
}
// 查询最大
int fmax(int u,int v){
int res = -1e9;
int tu = top[u], tv = top[v]; // u,v的链顶
while(tu != tv){ //不在同一条链
if(deep[tu]< deep[tv]){//先考虑较深节点
swap(tu,tv);
swap(u,v);
}
res=max(res,qmax(1,p[tu],p[u]));// 查询u节点到他的链顶
u = fa[tu]; // 跳到链顶的父节点
tu = top[u];// 更新链顶
}
if(deep[u] > deep[v]) swap(u,v);
res = max(res,qmax(1,p[u],p[v]));// 同一条链 直接区间查询
return res;
}
int n;
int main(){
scanf("%d",&n);
int fr,to;
init();
FOR(i,1,n-1){
scanf("%d%d",&fr,&to);
addedge(fr,to);
addedge(to,fr);
}
dfs1(1,0,0);
dfs2(1,1);
FOR(i,1,n) {
scanf("%d",&a[i]);
}
// FOR(i,1,n){
// printf("%d %d %d %d %d %d
",top[i],fa[i],deep[i],num[i],p[i],son[i]);
// }cout << endl;
build(1,1,n);
// FOR(i,1,n){
// update(1,i,i,a[p[i]]);
// }
int q;
char op[10];
scanf("%d",&q);
FOR(i,1,q){
scanf("%s%d%d",op,&fr,&to);
if(op[0]=='C'){
update(1,p[fr],p[fr],to);
}else if(op[1]=='M'){
printf("%d
",fmax(fr,to));
}else if(op[1]=='S'){
printf("%d
",fsum(fr,to));
}
}
return 0;
}