SPOJ QTREE2

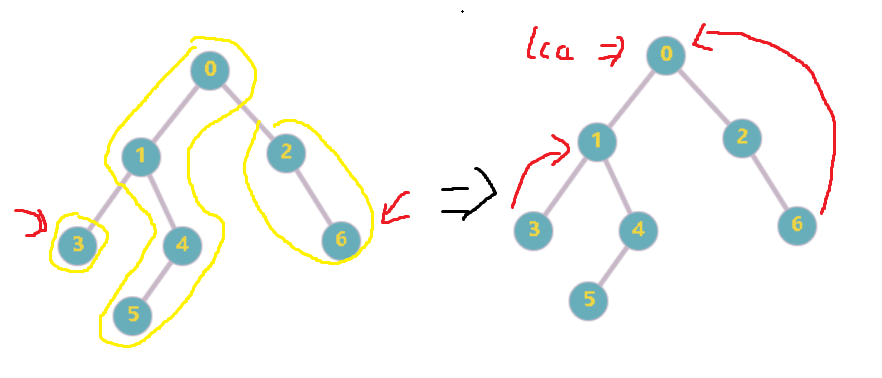
• 题意: 树上查询两点之间的距离和两点路径上的第k个点
• 思路: 先用树剖求lca,并记录下每个点到根的距离来回答第一个询问.
  对于第二个询问,求每个点到其lca的距离然后暴力向上跳,若deep[x]-deep[t]>=k-1,则在左边上跳(k-1)个点,否则在右边上跳deep[x]+deep[y]-2*deep[t]-k+1个点

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define ll long long
#define FOR(i,l,r) for(int i = l ; i <= r ;++i )
#define inf 1<<30
#define eps (1e-9)
#define ALL(T)  T.begin(),T.end()
#define lson(i)     i<<1
#define rson(i)     (i<<1|1)
using namespace std;
typedef pair<int,int> pii;
const int maxn = 100010;

struct Edge{
    int to,next,w;
}edge[maxn*2];

int head[maxn],tot;
int top[maxn],fa[maxn],deep[maxn],num[maxn],p[maxn],fp[maxn],son[maxn],val[maxn];
int pos;

void addedge(int u,int v,int w){
    edge[++tot].to = v;
    edge[tot].next = head[u];
    edge[tot].w = w;
    head[u] = tot;
}
void init(){
    memset(head,0,sizeof head);
    memset(son,-1,sizeof son);
    tot = 0;
    pos = 1;
}

void dfs1(int u,int pre,int d){
    deep[u] = d;
    fa[u] = pre;
    num[u] = 1;
    for(int i=head[u];i;i=edge[i].next){
        int v = edge[i].to;
        if(v!=pre){
            val[v] = val[u] + edge[i].w;
            dfs1(v,u,d+1);
            num[u] += num[v];
            if(son[u]==-1 || num[v] > num[son[u]]){
                son[u] = v;
            }
        }
    }
}
void dfs2(int u,int sp){
    top[u] = sp;
    p[u] = pos++;
    fp[p[u]] = u;
    if(son[u]== -1) return ;
    dfs2(son[u],sp);
    for(int i=head[u];i;i=edge[i].next){
        int v = edge[i].to;
        if(v!=son[u] && v!=fa[u])
            dfs2(v,v);
    }
}
int query(int x,int y){
    while(top[x]!=top[y]){
        if(deep[top[x]]>deep[top[y]]){
            x = fa[top[x]];
        }else{
            y = fa[top[y]];
        }
    }
    return deep[x] < deep[y] ? x:y;
}
int findf(int u,int k){
    while (k)
    {
        k--;
        u = fa[u];
    }
    return u;
}
int n,m,x,y,v;
char op[10];
int main(){
    int cas;
    scanf("%d",&cas);
    while(cas--){
        
    scanf("%d",&n);
    init();
    for(int i=1;i<n;++i){
        scanf("%d%d%d",&x,&y,&v);
        addedge(x,y,v);
        addedge(y,x,v);
    }
    dfs1(1,0,0);
    dfs2(1,1);
    for(int i=1;i<=m;++i){
    }
    while(scanf("%s",op)){
        if(op[1]=='I'){
            scanf("%d%d",&x,&y);
            int t = query(x,y);
            printf("%d
",val[x]+val[y]-2*val[t]);
        }else if(op[1]=='T'){
            scanf("%d%d%d",&x,&y,&v);
            int t = query(x,y);
            int r ;
            if(deep[x]-deep[t]>=v-1){
                r= findf(x,v-1);
            }else{
                r= findf(y,deep[y]-v+deep[x]-2*deep[t]+1);
            }
            printf("%d
",r);
        }else if(op[1]=='O'){
            break;
        }
    }
    
    }
    return 0;
}

树链剖分求lca

1. 两个点跳到同一链上(更深的点跳到他所在链链顶的父亲)
2. 深度更小的点为初始两个点的lca

感性理解下