1261. 在受污染的二叉树中查找元素

给出一个满足下述规则的二叉树：

root.val == 0
如果 treeNode.val == x 且 treeNode.left != null，那么 treeNode.left.val == 2 * x + 1
如果 treeNode.val == x 且 treeNode.right != null，那么 treeNode.right.val == 2 * x + 2
现在这个二叉树受到「污染」，所有的 treeNode.val 都变成了 -1。

请你先还原二叉树，然后实现 FindElements 类：

FindElements(TreeNode* root) 用受污染的二叉树初始化对象，你需要先把它还原。
bool find(int target) 判断目标值 target 是否存在于还原后的二叉树中并返回结果。
 

示例 1：

输入：
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
输出：
[null,false,true]
解释：
FindElements findElements = new FindElements([-1,null,-1]);
findElements.find(1); // return False
findElements.find(2); // return True
示例 2：

输入：
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
输出：
[null,true,true,false]
解释：
FindElements findElements = new FindElements([-1,-1,-1,-1,-1]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False
示例 3：

输入：
["FindElements","find","find","find","find"]
[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]
输出：
[null,true,false,false,true]
解释：
FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]);
findElements.find(2); // return True
findElements.find(3); // return False
findElements.find(4); // return False
findElements.find(5); // return True
 

提示：

TreeNode.val == -1
二叉树的高度不超过 20
节点的总数在 [1, 10^4] 之间
调用 find() 的总次数在 [1, 10^4] 之间
0 <= target <= 10^6

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-elements-in-a-contaminated-binary-tree

很容易想到递归建树，然后把值放在set()中，再递归查找

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class FindElements:
    def __init__(self, root: TreeNode):
        self.vis=set()
        def recover(node):
            if not node:
                return node
            if node.left:
                node.left.val=2*node.val+1
                self.vis.add(node.left.val)
            if node.right:
                node.right.val=2*node.val+2
                self.vis.add(node.right.val)
            recover(node.left)
            recover(node.right)
            return node
        root.val=0
        self.vis.add(0)
        self.node=recover(root)

    def find(self, target: int) -> bool:
        return target in self.vis
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)

然而

我就盲猜更好的解法是用二进制

然后猜不下去了

如果我们把树中的数全部加 1

 （图参考 https://leetcode.com/problems/find-elements-in-a-contaminated-binary-tree/discuss/431229/Python-Special-Way-for-find()-without-HashSet-O(1)-Space-O(logn)-Time）

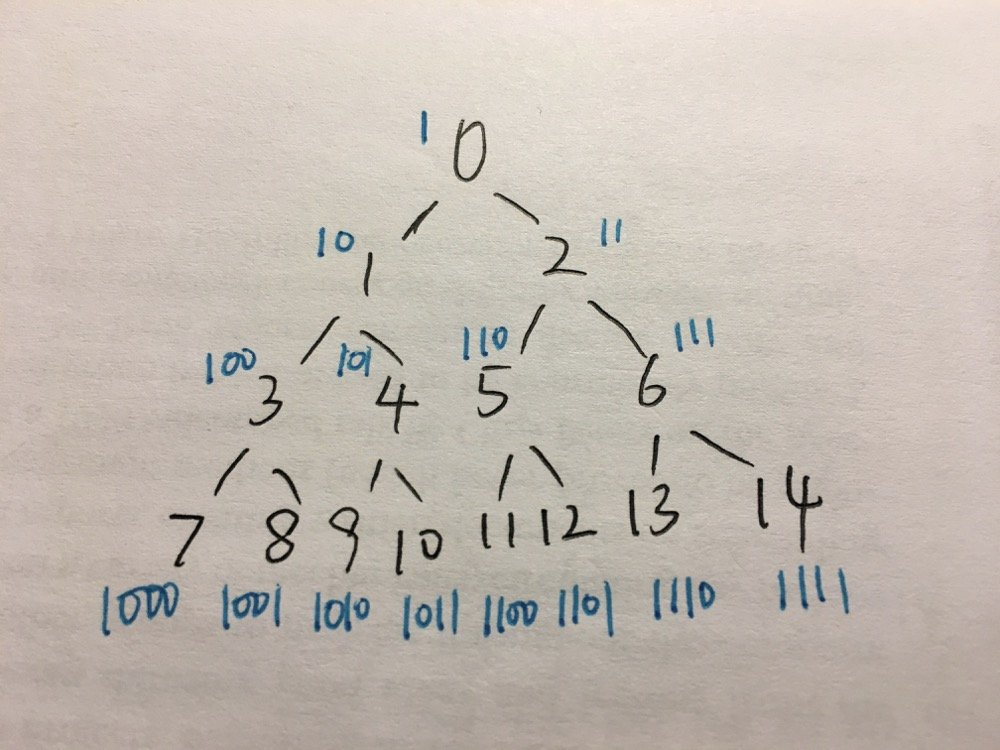
发现每一行的左右子树分别有不同的前缀：

 发现0是向左 ， 1是向右

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class FindElements:
    def __init__(self, root: TreeNode):
        def recover(node):
            if not node:
                return node
            if node.left:
                node.left.val=2*node.val+1
            if node.right:
                node.right.val=2*node.val+2
            recover(node.left)
            recover(node.right)
            return node
        root.val=0
        self.node=recover(root)

    def find(self, target: int) -> bool:
        node=self.node
        for binary in bin(target+1)[3:]:
            node=node and (node.left,node.right)[int(binary)]
        return bool(node)
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)

然后

。。。

分析一下复杂度，解法一时间复杂度 O(1)，解法二O(1)-Space-O(logn)-Time

总结：解法一空间换时间，解法二可以预防MLE