题目链接:
https://jzoj.net/senior/#main/show/6092
题目:

知识点--平面图转对偶图
在求最小割的时候,我们可以把平面图转为对偶图,用最短路来求最小割,这样会比dinic更快,但只是只用于网格图
网格图(平面图),即满足可以画在平面,且任意两条边的交点只能是边的顶点的图
性质:一个联通的平面图有$n$个点,$m$条边,$f$个面,那么有$f=m-n+2$
对于一个平面图,我们可以找到它的对偶图。做法是把每一个分割出来的面作为一个个顶点,两个面之间存在边并且仅当这两个面在原图中存在公共边,新连的边的边权就是公共边的边权
如图为例
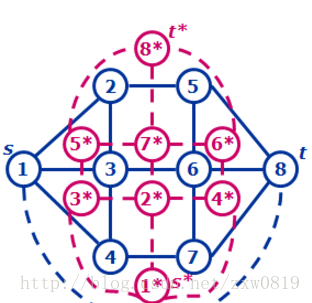
我们在下面找一个点$s*$,在上面找一个$t*$,在源点与汇点之间跑最短路即为原图的最小割。这个结论看起来蛮显然的
注意$s*$和$t*$要视情况而定来寻找(个人看法,我也没写过几道这样的题目,一般而言$dinic$优化一下就足够了)
那么如何把平面图转为对偶图呢?
我们对原图每一个点把连着它的边做极角排序。然后我们考虑一条边(有向),强制让它顺时针或者逆时针方向(这个都可以,但是每一条边定义的方向是要一样的,接下来就按顺时针来叙述),这样的话它的反向边就会朝另外一个方向,于是这样两个平面就建立起了双向边
其实最难的还是如何确定一个平面。设一条边起点为$u$,终点为$v$,这条边为$l$,做法是在顺时针转后在找到相对于v而言极角比l大的第一条边,很显然这样找到的边$r$和之前的边$l$就是同一个平面的两条相邻的边,那么我们就记下$nxt[l]=r$。弄完所有的边后,我们遍历每一条边并对取到的边标记,然后不断取$nxt$,知道取到又取到标记的边为止,这样我们就找到了一个面。口述比较难以理解,代码通俗易懂。值得注意的是这样我们也会把那个外面的无穷大平面找到
题解:
- 先把平面图转化为对偶图,在转化的过程中就可以算出每个平面的光明值和黑暗值,当然无限大的平面也可以算出
- 我们建一个超级源点S和一个超级汇点T,S向每个面连有向边,容量为其光明值,每个面向T连有向边,容量为其黑暗值。相邻的面之间连的是无向边,容量为其交边的c值
- 很显然答案为所有面的光明值和黑暗值之和减去这张图的最小割
- 归纳:这样每个元素有两个选择的很多都可以转化为最小割模型。并且由于最小割是最小化,若答案是最大化的化总是要用总的减去最小割的值(如最大权闭合子图模型)
代码:
#include<algorithm> #include<cstring> #include<iostream> #include<cmath> #include<cstdio> #include<vector> #include<queue> using namespace std; typedef long long ll; typedef double db; const int N=1e5+15; const int M=5e5+15; const ll inf=1e18; int n,m; inline char gc() { static char buf[1000000],*p1,*p2; if (p1==p2) p1=(p2=buf)+fread(buf,1,1000000,stdin); return p1==p2?EOF:*p2++; } inline ll read() { char ch=gc();ll s=0,f=1; while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=gc();} while (ch>='0'&&ch<='9') {s=(s<<3)+(s<<1)+ch-'0';ch=gc();} return s*f; } struct Point { int x,y,a,b; }p[N]; struct EDGE { int u,v,c; }edge[N<<1]; vector <int> t[N]; bool cmp(int a,int b) { int x1=p[edge[a].v].x-p[edge[a].u].x,y1=p[edge[a].v].y-p[edge[a].u].y; int x2=p[edge[b].v].x-p[edge[b].u].x,y2=p[edge[b].v].y-p[edge[b].u].y; return atan2((db)y1,(db)x1)<atan2((db)y2,(db)x2); } int tot; int vis[M],nxt[M],bel[M]; ll gms[M],has[M]; int cnt=1,T,S; int head[M]; ll sum; struct E { int to,nxt; ll cap; }e[M]; void adde(int u,int v,int c) { e[++cnt]=(E){v,head[u],c}; head[u]=cnt; } void insert(int u,int v,int c) { adde(u,v,c);adde(v,u,0); } void build()//平面图转对偶图 { for (int i=1;i<=n;i++) sort(t[i].begin(),t[i].end(),cmp); for (int i=0;i<(m<<1);i++) { int v=edge[i].v; vector<int>::iterator it=++lower_bound(t[v].begin(),t[v].end(),i^1,cmp); if (it==t[v].end()) it=t[v].begin(); nxt[i]=*it; } for (int i=0;i<(m<<1);i++) if (!vis[i]) { ++tot; for (int j=i;!vis[j];j=nxt[j]) vis[j]=1,bel[j]=tot; } //网络流建图 for (int i=0;i<(m<<1);i++) { int u=bel[i],v=bel[i^1],c=edge[i].c; gms[u]+=1ll*p[edge[i].u].a;has[u]+=1ll*p[edge[i].u].b; if (u>v) continue; adde(u,v,c);adde(v,u,c); } S=tot+1;T=tot+2; for (int i=1;i<=tot;i++) { sum+=gms[i]+has[i]; insert(S,i,gms[i]); insert(i,T,has[i]); } } queue <int> q; int dep[M]; int bfs() { while (!q.empty()) q.pop(); memset(dep,0,sizeof(dep)); dep[S]=1; q.push(S); while (!q.empty()) { int k=q.front();q.pop(); for (int i=head[k];i;i=e[i].nxt) { int y=e[i].to; if (e[i].cap&&!dep[y]) { dep[y]=dep[k]+1; q.push(y); } } } return dep[T]; } int cur[M]; ll dfs(int x,ll a) { if (x==T||!a) return a; ll f,flow=0; for (int &i=cur[x];i;i=e[i].nxt) { int y=e[i].to; if (dep[y]==dep[x]+1&&(f=dfs(y,min(e[i].cap,a)))>0) { flow+=f; a-=f; e[i].cap-=f; e[i^1].cap+=f; if (!a) break; } } return flow; } ll dinic() { ll res=0; while (bfs()) { memcpy(cur,head,sizeof(head)); res+=dfs(S,inf); } return res; } int main() { freopen("everfeel.in","r",stdin); freopen("everfeel.out","w",stdout); int NUM=read(); n=read();m=read(); for (int i=1;i<=n;i++) p[i].x=read(),p[i].y=read(),p[i].a=read(),p[i].b=read(); for (int i=0;i<m;i++) { int u=read(),v=read(),c=read(); edge[i<<1]=(EDGE){u,v,c};edge[i<<1|1]=(EDGE){v,u,c}; t[u].push_back(i<<1);t[v].push_back(i<<1|1); } build(); printf("%lld ",sum-dinic()); return 0; }