LeetCode——编辑距离

Q：给定两个单词word1和word2，请计算将word1转换为word2至少需要多少步操作。
你可以对一个单词执行以下3种操作：
a）在单词中插入一个字符
b）删除单词中的一个字符
c）替换单词中的一个字符

A：

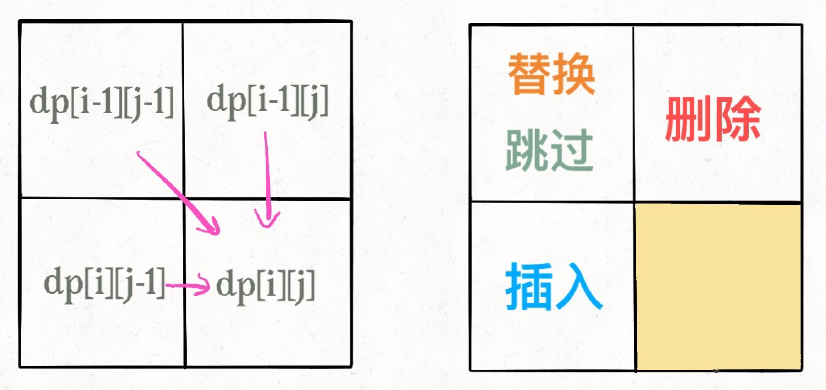
若 i == j,则意为着不需额外操作，则F(i,j) 显然 等于 F(i - 1,j - 1)
若 i != j,则肯定需要1步操作来转换
以 "ab" 到 "abc"为例，该最优解为： min{"a" 到 "abc"的最优解, "ab" 到 "ab"的最优解，"a" 到 "ab" 的最优解 } + 1
所以 该情况递推公式为：F(i,j) = min{F(i - 1, j), F(i, j - 1),F(i - 1, j - 1) } + 1

    public static int minDistance(String word1, String word2) {
        if (word1.isEmpty() && word2.isEmpty())
            return 0;
        int s1 = word1.length();
        int s2 = word2.length();
        int[][] dp = new int[s1 + 1][s2 + 1];
        for (int i = 0; i <= s1; i++) {
            dp[i][0] = i;
        }
        for (int j = 0; j <= s2; j++) {
            dp[0][j] = j;
        }
        for (int i = 1; i <= s1; i++) {
            for (int j = 1; j <= s2; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1))
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
            }
        }
        return dp[s1][s2];
    }