Q:给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
A:
1.常见错误(引用:@windliang)
根据回文串的定义,正着和反着读一样,那我们是不是把原来的字符串倒置了,然后找最长的公共子串就可以了。例如 S = "caba" ,S = "abac",最长公共子串是 "aba",所以原字符串的最长回文串就是 "aba"。
关于求最长公共子串(不是公共子序列),有很多方法,这里用动态规划的方法,
整体思想就是,申请一个二维的数组初始化为 0,然后判断对应的字符是否相等,相等的话 (arr [ i ][ j ] = arr [ i - 1 ][ j - 1] + 1) 。
当 i = 0 或者 j = 0 的时候单独分析,字符相等的话 (arr [ i ][ j ]) 就赋为 1 。
arr [ i ][ j ] 保存的就是公共子串的长度。
再看一个例子,S="abc435cba",S="abc534cba",最长公共子串是 "abc" 和 "cba",但很明显这两个字符串都不是回文串。
所以我们求出最长公共子串后,并不一定是回文串,我们还需要判断该字符串倒置前的下标和当前的字符串下标是不是匹配。
比如 S="caba",S'="abac" ,S’ 中 aba 的下标是 0 1 2 ,倒置前是 3 2 1,和 S 中 aba 的下标符合,所以 aba 就是我们需要找的。当然我们不需要每个字符都判断,我们只需要判断末尾字符就可以。
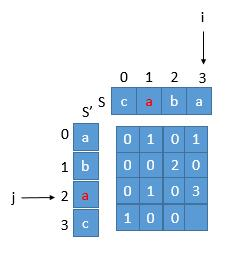
首先 i,j 始终指向子串的末尾字符。所以 j 指向的红色的 a 倒置前的下标是 beforeRev = length-1-j=4-1-2=1,对应的是字符串首位的下标,我们还需要加上字符串的长度才是末尾字符的下标,也就是 beforeRev+arr[i][j]-1=1+3-1=3,因为 arr[i][j] 保存的就是当前子串的长度,也就是图中的数字 3。此时再和它与 i 比较,如果相等,则说明它是我们要找的回文串。
之前的 S="abc435cba",S'="abc534cba",可以看一下图示,为什么不符合。

当前 j 指向的 c,倒置前的下标是 beforeRev=length-1-j=9-1-2=6,对应的末尾下标是beforeRev+arr[i][j]-1=6+3-1=8,而此时 i=2,所以当前的子串不是回文串。
算法:
我们可以看到,当 S 的其他部分中存在非回文子串的反向副本时,最长公共子串法就会失败。为了纠正这一点,每当我们找到最长的公共子串的候选项时,都需要检查子串的索引是否与反向子串的原始索引相同。如果相同,那么我们尝试更新目前为止找到的最长回文子串;如果不是,我们就跳过这个候选项并继续寻找下一个候选。
代码:
public String longestPalindrome(String s) {
if (s.length() == 0)
return "";
StringBuilder stringBuilder = new StringBuilder(s);
String s2 = stringBuilder.reverse().toString();//s反过来的
int[][] dp = new int[s.length()][s2.length()];
int maxLen = 0;
int maxEnd = 0;
for (int i = 0; i < s.length(); i++) {
for (int j = 0; j < s2.length(); j++) {
char c1 = s.charAt(i);
char c2 = s2.charAt(j);
if (i == 0 || j == 0) {
if (c1 == c2) {
dp[i][j] = 1;
}
} else {
if (c1 == c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
}
if (dp[i][j] > maxLen) {
int pre = s.length() - j - 1;//当前j对应的原始未反转前的index
if (pre + dp[i][j] - 1 == i) {//如果反转前的index开头的长度的子串正好可以到i,说明这个子串下标是对应的
maxLen = dp[i][j];
maxEnd = i;
}
}
}
}
return s.substring(maxEnd - maxLen + 1, maxEnd + 1);
}
2.动态规划法
但初始化的时候要注意,先是初始化对角线,即长度为1时;再是初始化长度为2时,即dp[i,i+1],因为如果只从1开始那只可能出现奇数长度的回文串。
代码:
public String longestPalindrome(String s) {
if (s.length() <= 1)
return s;
boolean[][] dp = new boolean[s.length()][s.length()];
int maxLen = 0;
String sub = String.valueOf(s.charAt(0));
for (int i = 0; i < s.length(); i++) {
Arrays.fill(dp[i], false);
dp[i][i] = true;//初始化长度为1的子串
if (i + 1 < s.length() && s.charAt(i) == s.charAt(i + 1)) {//初始化长度为2的子串
dp[i][i + 1] = true;
if (maxLen < 2) {
maxLen = 2;
sub = s.substring(i, i + 2);
}
}
}
for (int i = s.length() - 3; i >= 0; i--) {//动态规划里斜着遍历的情况
for (int j = i + 2; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1];
}
if (dp[i][j]) {
if (j - i + 1 > maxLen) {
maxLen = j - i + 1;
sub = s.substring(i, j + 1);
}
}
}
}
return sub;
}
3.扩散中心
知道回文串一定是对称的,所以我们可以每次循环选择一个中心,进行左右扩展,判断左右字符是否相等即可。
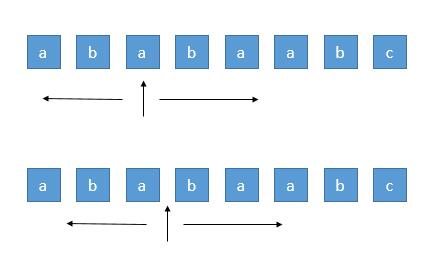
还是要注意初始长度为1或2.
代码:
public String longestPalindrome(String s) {
if (s.length() <= 1)
return s;
String sub1 = expand(s, 1);
String sub2 = expand(s, 2);
String sub = sub1.length() > sub2.length() ? sub1 : sub2;
return sub;
}
private String expand(String s, int len) {
int maxLen = 0;
String sub = String.valueOf(s.charAt(0));
for (int i = 0; i < s.length(); i++) {
int left = i;
int right = i + len - 1;
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
if (right - left + 1 > maxLen) {
maxLen = right - left + 1;
sub = s.substring(left, right + 1);
}
left--;
right++;
}
}
return sub;
}
4.Manacher's Algorithm 马拉车算法
马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法,由一个叫 Manacher 的人在 1975 年发明的,这个方法的最大贡献是在于将时间复杂度提升到了线性。
因为仅用于找回文子串,借鉴性不大,因此之后补。