Q:有 n 个气球,编号为0 到 n-1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。每当你戳破一个气球 i 时,你可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后,气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。
说明:
你可以假设 nums[-1] = nums[n] = 1,但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
示例:
输入: [3,1,5,8]
输出: 167
解释: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
A:
1.回溯法
但超时了。
private int res;
public int maxCoins(int[] nums) {
if (nums.length == 0)
return 0;
res = Integer.MIN_VALUE;
ArrayList<Integer> num = new ArrayList<>();
num.add(1);
for (int i : nums)
num.add(i);
num.add(1);
backTrace(num, 0);
return res;
}
private void backTrace(ArrayList<Integer> num, int sum) {
if (num.size() == 2) {
res = Math.max(res, sum);
return;
}
for (int i = 1; i < num.size() - 1; i++) {
sum += num.get(i - 1) * num.get(i) * num.get(i + 1);
int temp = num.get(i);
num.remove(i);
backTrace(num, sum);
num.add(i, temp);
sum -= num.get(i - 1) * num.get(i) * num.get(i + 1);
}
}
2.动态规划
引用自《labuladong的算法》
这个动态规划问题和我们之前的动态规划系列文章相比有什么特别之处?为什么它比较难呢?
原因在于,这个问题中我们每戳破一个气球nums[i],得到的分数和该气球相邻的气球nums[i-1]和nums[i+1]是有相关性的。
那么我们可以改变问题:在一排气球points中,请你戳破气球0和气球n+1之间的所有气球(不包括0和n+1),使得最终只剩下气球0和气球n+1两个气球,最多能够得到多少分?
现在可以定义dp数组的含义:
dp[i][j] = x表示,戳破气球i和气球j之间(开区间,不包括i和j)的所有气球,可以获得的最高分数为x。
那么根据这个定义,题目要求的结果现在我们要根据这个dp数组来推导状态转移方程了,根据我们前文的套路,所谓的推导「状态转移方程」,实际上就是在思考怎么「做选择」,也就是这道题目最有技巧的部分:
不就是想求戳破气球i和气球j之间的最高分数吗,如果「正向思考」,就只能写出前文的回溯算法;我们需要「反向思考」,想一想气球i和气球j之间最后一个被戳破的气球可能是哪一个?
其实气球i和气球j之间的所有气球都可能是最后被戳破的那一个,不防假设为k。回顾动态规划的套路,这里其实已经找到了「状态」和「选择」:i和j就是两个「状态」,最后戳破的那个气球k就是「选择」。
根据刚才对dp数组的定义,如果最后一个戳破气球k,dp[i][j]的值应该为:就是dp[0][n+1]的值,而 base case 就是dp[i][j] = 0,其中0 <= i <= n+1, j <= i+1,因为这种情况下,开区间(i, j)中间根本没有气球可以戳。
dp[i][j] = dp[i][k] + dp[k][j]
+ points[i]*points[k]*points[j]
你不是要最后戳破气球k吗?那得先把开区间(i, k)的气球都戳破,再把开区间(k, j)的气球都戳破;最后剩下的气球k,相邻的就是气球i和气球j,这时候戳破k的话得到的分数就是points[i]*points[k]*points[j]。
那么戳破开区间(i, k)和开区间(k, j)的气球最多能得到的分数是多少呢?嘿嘿,就是dp[i][k]和dp[k][j],这恰好就是我们对dp数组的定义嘛!
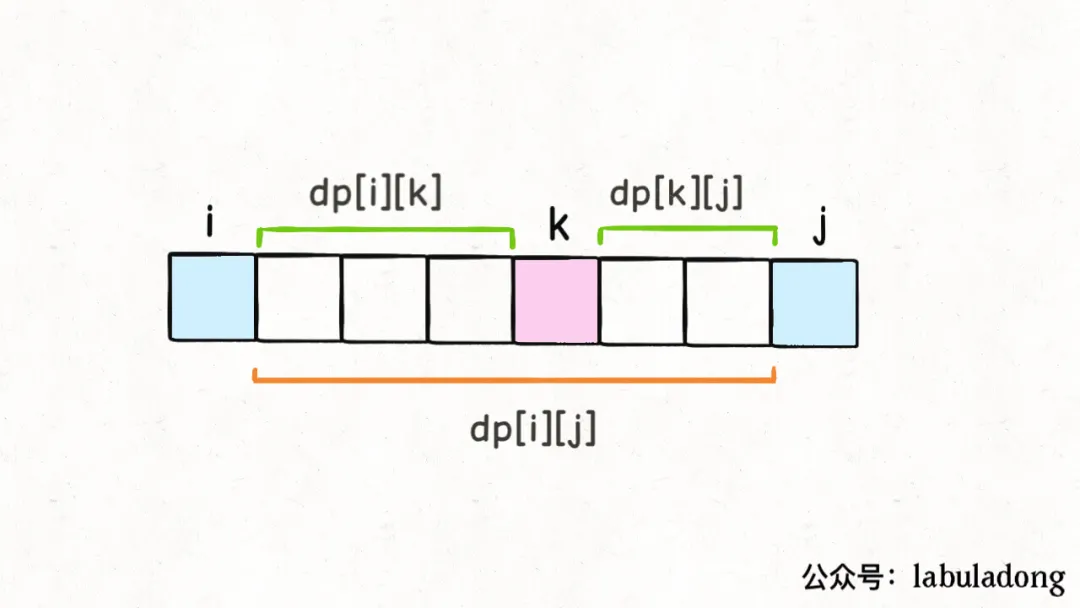
结合这个图,就能体会出dp数组定义的巧妙了。由于是开区间,dp[i][k]和dp[k][j]不会影响气球k;而戳破气球k时,旁边相邻的就是气球i和气球j了,最后还会剩下气球i和气球j,这也恰好满足了dp数组开区间的定义。
那么,对于一组给定的i和j,我们只要穷举i < k < j的所有气球k,选择得分最高的作为dp[i][j]的值即可,这也就是状态转移方程:
// 最后戳破的气球是哪个?
for (int k = i + 1; k < j; k++) {
// 择优做选择,使得 dp[i][j] 最大
dp[i][j] = Math.max(
dp[i][j],
dp[i][k] + dp[k][j] + points[i]*points[j]*points[k]
);
}
根据 base case 和最终状态进行推导。最终状态就是指题目要求的结果,对于这道题目也就是dp[0][n+1]。
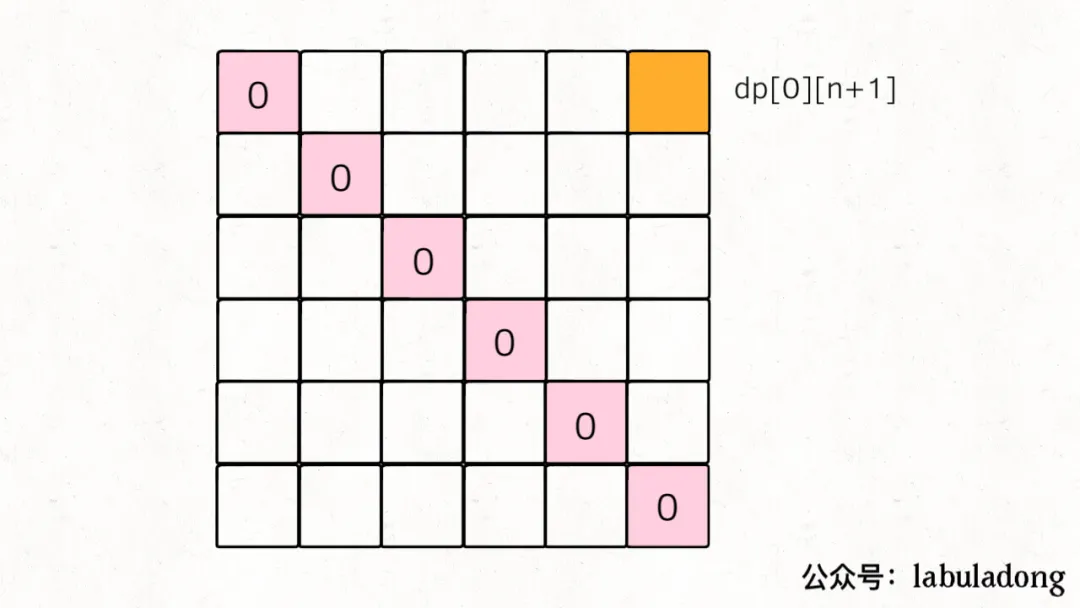
代码:
public int maxCoins(int[] nums) {
if (nums.length == 0)
return 0;
int n = nums.length;
int[] points = new int[n + 2];//加头加尾
points[0] = 1;
points[n + 1] = 1;
for (int i = 0; i < n; i++) {
points[i + 1] = nums[i];
}
int[][] dp = new int[n + 2][n + 2];
for (int i = 0; i < n + 2; i++) {
dp[i][i] = 0;//对角线base
}
for (int i = n; i >= 0; i--) {
for (int j = i + 1; j < n + 2; j++) {//斜着遍历
for (int k = i + 1; k < j; k++) {
dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + points[k] * points[i] * points[j]);//状态转移
}
}
}
return dp[0][n + 1];
}