1. Wiggle Walk
Q:在R*C的正方形当中有一个位于(S_R, S_C)机器人,给机器人N个上下左右(NSWE)移动一格的命令,如果机器人移动到之前到达过的位置,则继续朝原方向移动一格(保证机器人不会移出正方形)。按命令最后终点在哪里。

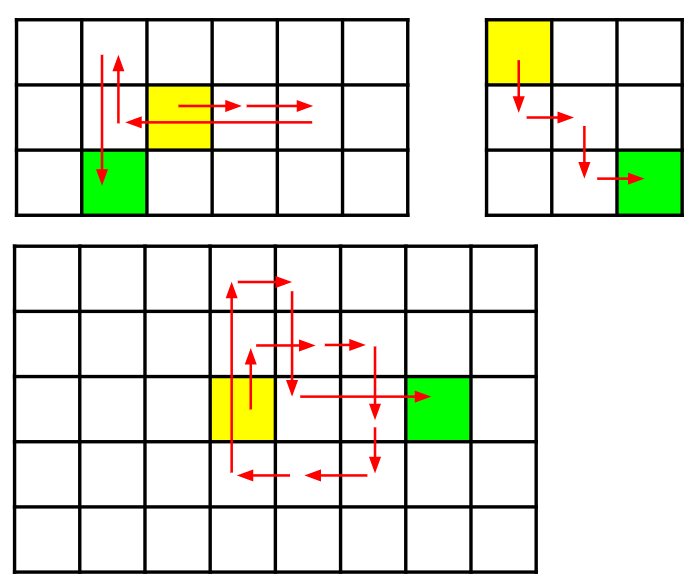
A:四个解法:
- 暴力模拟
- 使用HashMap优化,理论时间复杂度最小(好像也是并查集)
- (推荐)使用BitSet,实际占用空间特别小,仅仅是 2mn 个比特大小
- 使用HashMap实现的并查集方法,在东南西北4个方向上用并查集处理。因为机器人落脚点都是联通的,所以可以维护一个dict_XY用于记录从x,y往direct方向走会到达dict_XY[(X, Y)][direct]点。这个变量初始时候是x,y相邻的四个点,但是在机器人移动的过程中会进行更新,更新的思想有点像并查集。最后考虑到极端情况下用N*N个状态来表示格子会超空间限制,所以需要使用map来表示格子的状态。最终算法的复杂度为O(NlogN)
2. Circuit Board
Q:给定一个 (R imes C) 大小的矩阵,求其中最大的矩形,满足每一行的极差(最大值和最小值的差)不超过 (K)。题解
A:我们可以针对每一行来进行考虑。针对每一行,如果我们决定了列数(即决定了最右侧的起始列),那么我们可以从这一列出发找到以这一列最长的矩形使得极差满足题目要求。有了上面的观察,我们现在把这个矩阵转置一下,那么我们之前找到的矩形变成了什么?直方图(或者叫柱状图)!而对于一个确定的直方图找最大的矩形面积已经是一个经典问题了,简单的单调栈就可以了。
3. Catch Some
Q:在一条一维沿 (x) 轴正方向的数轴上有 (N) 条狗,每条狗在不同的位置且是不同的颜色。Bundle 想要观察 这些狗,规则是当且仅当 Bundle 身上穿的 T 恤颜色和狗的颜色相同时,狗才会出现。Bundle 只能在家里换 T 恤,Bundle 的家在 (x=0) 的位置。假如 Bundle 想要观察 (K) 条狗,最短的时间是多少?其中,每移动(向左向右)消耗 (1) 个单位时间,换 T 恤不消耗任何时间。
A:一个简单的观察是,针对每种颜色,我们只会穿一次 T 恤,而不会来回换;另一个观察是,如果我们不考虑我们最后一次观察(可以不用回家),我们观察某种颜色的狗 (k) 只所需要的时间是这条狗的位置乘以 (2)。这启发我们这么设计状态:( ext{dp}[i][j]) 表示对于前 (1sim i) 种颜色,我们观察了 (j) 条狗所用的最短时间。那么,转移方程实际上非常容易写出来:
其中 ( ext{len}(t_i)) 表示颜色为 (i) 的狗的数目,而 (t_{i,k}) 代表按升序排列后,颜色为 (i) 的第 (k) 条狗所在的位置。上述过程是 (mathcal{O}(N^2)) 的。然而,我们漏了一个点:最后观察的狗的颜色。那么,我们还需要枚举最后观察的狗的颜色,根据这个颜色来修改 dp 过程,总复杂度扩展到了 (mathcal{O}(N^3)),只能通过 Visible Set。现在我们来扩展状态:( ext{dp}[i][j][0/1]) 表示对于前 (1sim i) 种颜色,我们观察了 (j) 条狗所用的最短时间。其中,当第三位为 (0) 时,代表我们 (1sim i) 中没有任何一种颜色是我们最后观察的,而 (1) 则相反。那么 ( ext{dp}[i][j][0]) 的方程不变,我们来讨论 ( ext{dp}[i][j][1]) 的方程。容易观察到,( ext{dp}[i][j][1]) 包含两种情况:前面已经有了最后观察的颜色,和当前这种颜色是最后观察的颜色。那么,如果我们前面已经有了最后观察的颜色,当前的颜色必然是要回家的,所以是 ( ext{dp}[i-1][j-k][1]+2 imes t_{i,k});而假如前面没有遇到过最后观察的颜色,那么我们当前的颜色就不需要回家,直接观察完就可以了,所以是 ( ext{dp}[i-1][j-k][0]+t_{i,k})。所以最后总的方程就是:
答案就是 ( ext{dp}[c][K][1]),其中 (c) 是不同的颜色的数目。离散化一下狗的种类,然后直接 dp 就可以了。复杂度 (mathcal{O}(N^2))。