LeetCode——课程安排 IV

Q：你总共需要上 n 门课，课程编号依次为 0 到 n-1 。
有的课会有直接的先修课程，比如如果想上课程 0 ，你必须先上课程 1 ，那么会以 [1,0] 数对的形式给出先修课程数对。
给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。
对于每个查询对 queries[i] ，请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。
请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。
注意：如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程。

示例 2：
输入：n = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

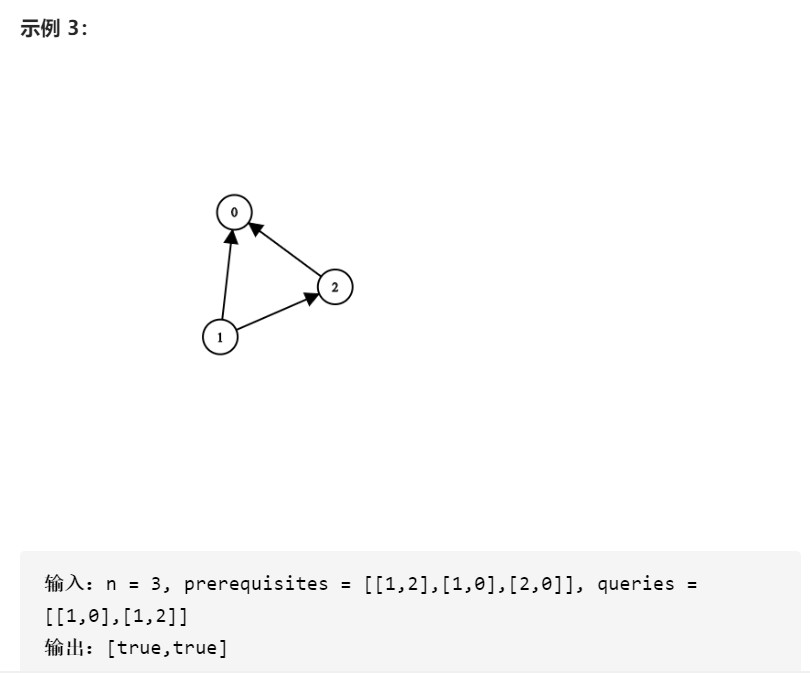
示例 4：
输入：n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
输出：[false,true]
示例 5：
输入：n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
输出：[true,false,true,false]
 
提示：
2 <= n <= 100
0 <= prerequisite.length <= (n * (n - 1) / 2)
0 <= prerequisite[i][0], prerequisite[i][1] < n
prerequisite[i][0] != prerequisite[i][1]
先修课程图中没有环。
先修课程图中没有重复的边。
1 <= queries.length <= 10^4
queries[i][0] != queries[i][1]

A：

1. DFS+Memo

    public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
        Map<Integer, Set<Integer>> graph = new HashMap<>();
        for (int[] pre : prerequisites) {
            Set<Integer> set = graph.getOrDefault(pre[0], new HashSet<>());
            set.add(pre[1]);
            graph.put(pre[0], set);
        }
        List<Boolean> ret = new ArrayList<>();
        boolean[][] isCalculated = new boolean[n][n];//一个用来记录计没计算过
        boolean[][] cache = new boolean[n][n];//一个用来记录计算后的结果
        for (int[] query : queries) {
            ret.add(dfs(query[0], query[1], graph, isCalculated, cache));
        }
        return ret;
    }

    private Boolean dfs(int start, int target, Map<Integer, Set<Integer>> graph, boolean[][] isCalculated, boolean[][] cache) {
        if (isCalculated[start][target])
            return cache[start][target];
        isCalculated[start][target] = true;
        if (start == target)
            return cache[start][target] = true;
        if (!graph.containsKey(start)) {
            return cache[start][target] = false;
        }
        for (int ch : graph.get(start)) {
            isCalculated[start][ch] = true;
            cache[start][ch] = true;
            if(dfs(ch, target, graph, isCalculated, cache))
                return cache[start][target] = true;
        }
        return cache[start][target] = false;
    }

2. 有DFS，就有BFS，同样用一个memo记录是否访问过

    public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
        Map<Integer, Set<Integer>> graph = new HashMap<>();
        for (int[] pre : prerequisites) {
            Set<Integer> set = graph.getOrDefault(pre[0], new HashSet<>());
            set.add(pre[1]);
            graph.put(pre[0], set);
        }
        List<Boolean> ret = new ArrayList<>();
        for (int[] query : queries) {
            ret.add(bfs(n, query[0], query[1], graph));
        }
        return ret;
    }

    private Boolean bfs(int n, int start, int target, Map<Integer, Set<Integer>> graph) {
        if (start == target || (graph.containsKey(start) && graph.get(start).contains(target)))
            return true;
        if (!graph.containsKey(start)) {
            return false;
        }
        boolean[] visited = new boolean[n];
        Arrays.fill(visited, false);
        Queue<Integer> q = new LinkedList<>();
        q.add(start);
        while (!q.isEmpty()) {
            int curr = q.poll();
            Set<Integer> set = graph.getOrDefault(start, new HashSet<>());
            set.add(curr);
            graph.put(start, set);
            if(curr == target)
                return true;
            else{
                if(!visited[curr]){
                    visited[curr] = true;
                    if(graph.containsKey(curr)){
                        Set<Integer> temp = graph.get(curr);
                        q.addAll(temp);
                    }
                }
            }
        }
        return false;
    }

3. floyd-warshall算法（该算法其实是用来求最短路的），又名打表法：
   有向图的传递闭包：给定有向图G=(V,E)，我们希望判断对于所有结点对i,j,图G是否包含一条对节点i,j的路径。
   传递闭包具有传递性，即如果i->j，j->k，那么i->k。具体来说，对于边(u,v)，枚举所有形如(j,u)的边，若(j,u)存在边，即j->u，那么由于u->v，那么j->v。
   用于该题，即对于每个prerequisite，i->l 那么 i->l->r 即i->1；r->j 那么 l->r->j 即l->j

    public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
        boolean[][] arr = new boolean[n][n];
        for (int[] p : prerequisites) {
            int l = p[0], r = p[1];
            arr[l][r] = true;
            for (int i = 0; i < n; i++) {
                if (arr[i][l])
                    arr[i][r] = true;
            }
            for (int j = 0; j < n; j++) {
                if (arr[r][j])
                    arr[l][j] = true;
            }
        }
        List<Boolean> res = new ArrayList<>();
        for (int[] q : queries) {
            res.add(arr[q[0]][q[1]]);
        }
        return res;
    }