\(\color{#FF003F}{\texttt {CF1336F Journey}}\)
对两条链的 \(\operatorname {lca}\) 是否相同进行分类讨论。下面 \(x\) 的链指 \(\operatorname {lca}(s,t)=x\) 的链,链 \((s,t)\) 需要满足 \(dfn_s<dfn_t\)。
- 如果\(\operatorname {lca}\)不同。
dfs整颗树,并在 \(\operatorname {lca}\) 的深度较浅处产生贡献。这样做的好处是 两条链的交一定是 在深度较深的链上的一条以\(\operatorname {lca}\)为端点的链,树状树组统计。
具体地,dfs到一个点 \(x\) 时,先递归处理儿子,再统计 \(x\) 和子树内的链的贡献。
放张官方sol的图。
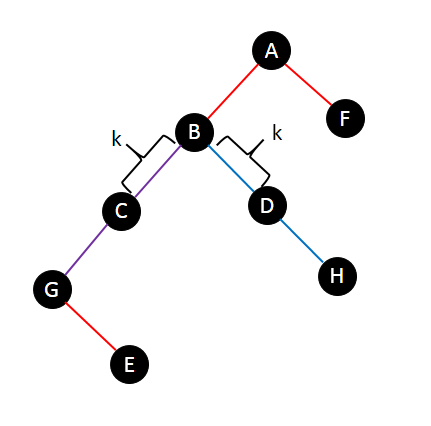
图中有两条链,E-F和G-H,他们的交是B-G,且B-C和B-D的距离是k。
处理G-H的时候,对C,D做子树加,在E-F统计答案的时候,查询E,F的值。
- 如果 \(\operatorname {lca}\) 相同。
枚举每个点作为\(\operatorname {lca}\)。当前点是 \(x\)。将 \(x\) 的所有链的 \(s\) 端点建棵虚树,\(t\) 端点存在 \(s\) 上。
设 \(\operatorname {lca}(x1,x2)=a\),从 \(a\) 向 \(y1\) 走 \(k\) 步到点 \(u\),所有合法的 \(y2\) 在 \(u\) 的子树内。
启发式合并+线段树合并维护。
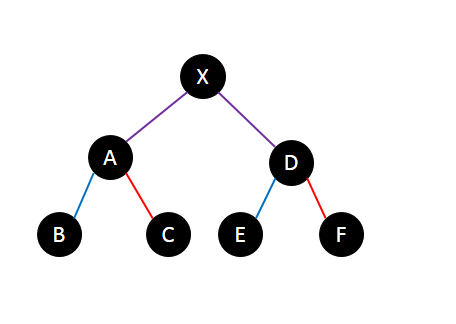
图中有两条链,B-E和C-F,他们的交是A-D,且A-X的距离是k。
\(\operatorname {lca}(B,C)=A\),A向E走 \(k\) 步到X,查询X的子树内的 \(y\) 点,点F产生贡献。
- 这样做还遗漏了一种情况
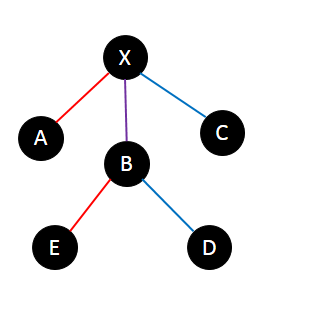
图中有2条链,A-E和C-D,他们的交是B-X。
其中 \(dfn_A<dfn_E<dfn_D<dfn_C\),容易发现这对链没被上面两种情况包含。
对于这种情况,把当前点的链按 \(dfn_s\) 排序,此时链的交一定是从lca向下的一条链,用类似第1种情况的方法统计即可。
复杂度 \(O(mlog^2n+nlogn)\),瓶颈在于启发式合并。
// Author -- xyr2005
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-(x)))
#define DEBUG fprintf(stderr,"Running on Line %d in Function %s\n",__LINE__,__FUNCTION__)
#define SZ(x) ((int)x.size())
#define mkpr std::make_pair
#define pb push_back
typedef long long ll;
typedef unsigned int uint;
typedef unsigned long long ull;
typedef std::pair<int,int> pi;
typedef std::pair<ll,ll> pl;
using std::min;
using std::max;
const int inf=0x3f3f3f3f,Inf=0x7fffffff;
const ll INF=0x3f3f3f3f3f3f3f3f;
std::mt19937 rnd(std::chrono::steady_clock::now().time_since_epoch().count());
template <typename _Tp>_Tp gcd(const _Tp &a,const _Tp &b){return (!b)?a:gcd(b,a%b);}
template <typename _Tp>inline _Tp abs(const _Tp &a){return a>=0?a:-a;}
template <typename _Tp>inline void chmax(_Tp &a,const _Tp &b){(a<b)&&(a=b);}
template <typename _Tp>inline void chmin(_Tp &a,const _Tp &b){(b<a)&&(a=b);}
template <typename _Tp>inline void read(_Tp &x)
{
char ch(getchar());bool f(false);while(!isdigit(ch)) f|=ch==45,ch=getchar();
x=ch&15,ch=getchar();while(isdigit(ch)) x=(((x<<2)+x)<<1)+(ch&15),ch=getchar();
f&&(x=-x);
}
template <typename _Tp,typename... Args>inline void read(_Tp &t,Args &...args){read(t);read(args...);}
inline int read_str(char *s)
{
char ch(getchar());while(ch==' '||ch=='\r'||ch=='\n') ch=getchar();
char *tar=s;*tar=ch,ch=getchar();while(ch!=' '&&ch!='\r'&&ch!='\n'&&ch!=EOF) *(++tar)=ch,ch=getchar();
return tar-s+1;
}
const int N=150005;
int n;
struct edge{
int v,nxt;
}c[N<<1];
int front[N],edge_cnt;
inline void addedge(int u,int v)
{
c[++edge_cnt]=(edge){v,front[u]};
front[u]=edge_cnt;
}
int anc[N][21],dep[N],siz[N],dfn[N],rev[N],id;
struct seg_tr{
struct Node{
int ls,rs,sum;
}f[N<<5];
int node_cnt;
int st[N<<5],top;
inline void PushUp(int x){f[x].sum=f[f[x].ls].sum+f[f[x].rs].sum;}
inline int newnode()
{
int cur=top?st[top--]:++node_cnt;
f[cur]=(Node){0,0,0};
return cur;
}
void Update(int &cur,int l,int r,int pos)
{
if(!cur) cur=newnode();
++f[cur].sum;
if(l==r) return;
int mid=(l+r)>>1;
if(pos<=mid) Update(f[cur].ls,l,mid,pos);
else Update(f[cur].rs,mid+1,r,pos);
}
int Query(int L,int R,int l,int r,int cur)
{
if(!cur) return 0;
if(L<=l&&r<=R) return f[cur].sum;
int mid=(l+r)>>1;
return (L<=mid?Query(L,R,l,mid,f[cur].ls):0)+(R>mid?Query(L,R,mid+1,r,f[cur].rs):0);
}
int merge(int a,int &b)
{
if(!a||!b) return a|b;
f[a].sum+=f[b].sum;
f[a].ls=merge(f[a].ls,f[b].ls);
f[a].rs=merge(f[a].rs,f[b].rs);
st[++top]=b,b=0;
return a;
}
void del(int &x)
{
if(!x) return;
del(f[x].ls),del(f[x].rs);
st[++top]=x,x=0;
}
}tr;
int Fa[N];
void dfs1(int x,int fa)
{
dep[x]=dep[fa]+1,anc[x][0]=fa,Fa[x]=fa,siz[x]=1;
for(int i=1;i<=20;++i) anc[x][i]=anc[anc[x][i-1]][i-1];
dfn[x]=++id,rev[x]=id;
for(int i=front[x];i;i=c[i].nxt)
{
int v=c[i].v;
if(v!=fa) dfs1(v,x),siz[x]+=siz[v];
}
}
int jump(int x,int k)
{
for(int i=20;i>=0;--i) if((k>>i)&1) x=anc[x][i];
return x;
}
int lca(int x,int y)
{
if(dep[x]<dep[y]) std::swap(x,y);
for(int i=20;i>=0;--i) if(dep[anc[x][i]]>=dep[y]) x=anc[x][i];
if(x==y) return x;
for(int i=20;i>=0;--i) if(anc[x][i]!=anc[y][i]) x=anc[x][i],y=anc[y][i];
return anc[x][0];
}
ll ans;
int k;
struct BIT{
int c[N];
inline void clear(){memset(c,0,sizeof(c));}
inline void add(int x,int C){++x;for(;x<N;x+=lowbit(x))c[x]+=C;}
inline int sum(int x){++x;int ans=0;for(;x;x-=lowbit(x))ans+=c[x];return ans;}
}_tr;
struct node{
int x,y;
inline bool operator < (const node &o)const{return dfn[x]<dfn[o.x];}
};
std::vector<node> v[N];
void dfs2(int x,int fa)
{
for(int i=front[x];i;i=c[i].nxt)
{
int v=c[i].v;
if(v!=fa) dfs2(v,x);
}
for(auto it:v[x]) ans+=_tr.sum(dfn[it.x])+_tr.sum(dfn[it.y]);
for(auto it:v[x])
{
if(dep[it.x]-dep[x]>=k)
{
int qwq=jump(it.x,dep[it.x]-dep[x]-k);
_tr.add(dfn[qwq],1),_tr.add(dfn[qwq]+siz[qwq],-1);
}
if(dep[it.y]-dep[x]>=k)
{
int qwq=jump(it.y,dep[it.y]-dep[x]-k);
_tr.add(dfn[qwq],1),_tr.add(dfn[qwq]+siz[qwq],-1);
}
}
}
int t[N],pos,st[N],top;
std::vector<int> e[N],q[N];
int root[N];
void ins(int x)
{
if(!top||(dfn[x]>=dfn[st[top]]&&dfn[x]<dfn[st[top]]+siz[st[top]]))
{
t[++pos]=x,st[++top]=x;
return;
}
int l=lca(x,st[top]);
while(top>1&&dfn[st[top-1]]>=dfn[l]) e[st[top-1]].pb(st[top]),--top;
if(st[top]!=l) e[l].push_back(st[top]),st[top]=l,t[++pos]=l;
st[++top]=x,t[++pos]=x;
}
int cur_node;
std::vector<int> in[N];
void dfs3(int x)
{
std::function<void(int)> merge=[&](int a)
{
if(in[a].size()>in[x].size()) std::swap(in[a],in[x]),std::swap(root[a],root[x]);
for(auto it:in[a])
{
int qwq;
if(dep[x]-dep[cur_node]>=k) qwq=cur_node;
else
{
int len=dep[x]+dep[it]-(dep[cur_node]<<1);
if(len<k) continue;
qwq=jump(it,len-k);
}
ans+=tr.Query(dfn[qwq],dfn[qwq]+siz[qwq]-1,1,n,root[x]);
}
for(auto it:in[a]) in[x].push_back(it);
in[a].clear();
root[x]=tr.merge(root[x],root[a]);
};
for(auto it:q[x])
{
int qwq;
if(dep[x]-dep[cur_node]>=k) qwq=cur_node;
else
{
int len=dep[x]+dep[it]-(dep[cur_node]<<1);
if(len>=k) qwq=jump(it,len-k);
else qwq=0;
}
if(qwq) ans+=tr.Query(dfn[qwq],dfn[qwq]+siz[qwq]-1,1,n,root[x]);
tr.Update(root[x],1,n,dfn[it]);
in[x].push_back(it);
}
for(auto it:e[x]) dfs3(it),merge(it);
}
void solve(int x)
{
cur_node=x,top=0,pos=0;
std::vector<int> nd;
for(auto it:v[x]) nd.pb(it.x),q[it.x].pb(it.y);
nd.erase(std::unique(nd.begin(),nd.end()),nd.end());
for(auto it:nd) ins(it);
while(top>1) e[st[top-1]].pb(st[top]),--top;
int minn=inf,id=0;
for(int i=1;i<=pos;++i) if(dfn[t[i]]<minn) minn=dfn[t[i]],id=t[i];
if(id) dfs3(id);
for(auto it:v[x]) q[it.x].clear();
for(int i=1;i<=pos;++i) tr.del(root[t[i]]),in[t[i]].clear(),e[t[i]].clear();
}
void _solve(int x)
{
std::vector<int> tmp;
for(auto it:v[x])
{
ans+=_tr.sum(dfn[it.x]);
if(dep[it.y]-dep[x]>=k)
{
int qwq=jump(it.y,dep[it.y]-dep[x]-k);
_tr.add(dfn[qwq],1),_tr.add(dfn[qwq]+siz[qwq],-1);
tmp.push_back(qwq);
}
}
for(auto qwq:tmp) _tr.add(dfn[qwq],-1),_tr.add(dfn[qwq]+siz[qwq],1);
}
int main()
{
int m;read(n,m,k);
int x,y;
for(int i=1;i<n;++i) read(x,y),addedge(x,y),addedge(y,x);
dfs1(1,0);
for(int i=1;i<=m;++i)
{
read(x,y);
if(dfn[x]>dfn[y]) std::swap(x,y);
v[lca(x,y)].pb((node){x,y});
}
dfs2(1,0);
_tr.clear();
for(int i=1;i<=n;++i) std::sort(v[i].begin(),v[i].end());
for(int i=1;i<=n;++i) _solve(i);
for(int i=1;i<=n;++i) solve(i);
printf("%lld\n",ans);
return 0;
}