题目大意
有一棵(n)((nleq10^5))个点的树,每个点(i)有颜色(c_i)((c_ileq10^5))
定义一条路径的得分为这条路径上的不同颜色个数
分别求每个点的以该点出发的所有路径的得分总和
题解
统计和路径有关的东西,让人想到点分治
找到当前区域的重心后,计算所有过重心的路径的影响
记每个当前区域里的点(i)以重心为根时,当前区域里的子树大小为(siz_i)
先分别算出每个颜色(i),对“从重心出发的所有路径的得分总和”的贡献(W_i)
发现如果一个点(i)的颜色(c_i)是从重心到它的路径上第一次出现的,那么它对于每条“以重心为起点,以它子树里的点为终点”的路径都会产生1的贡献,即(W_{c_i}+=siz_i)
然后遍历当前区域,对于每种颜色(i),记(w_i)表示当前遍历的重心的儿子的子树里,颜色(i)对(W_i)的贡献为(w_i)(也就是说,(W_i-w_i)表示颜色(i)对“从重心出发的所有不经过当前遍历的重心的儿子路径的得分总和”的贡献)
记(x)表示过重心的路径对当前遍历到的点的贡献,初始值为(Sigma (W_i-w_i))
如果当前点(i)的颜色不是在重心到它的路径上第一次出现的,那么(x)不变
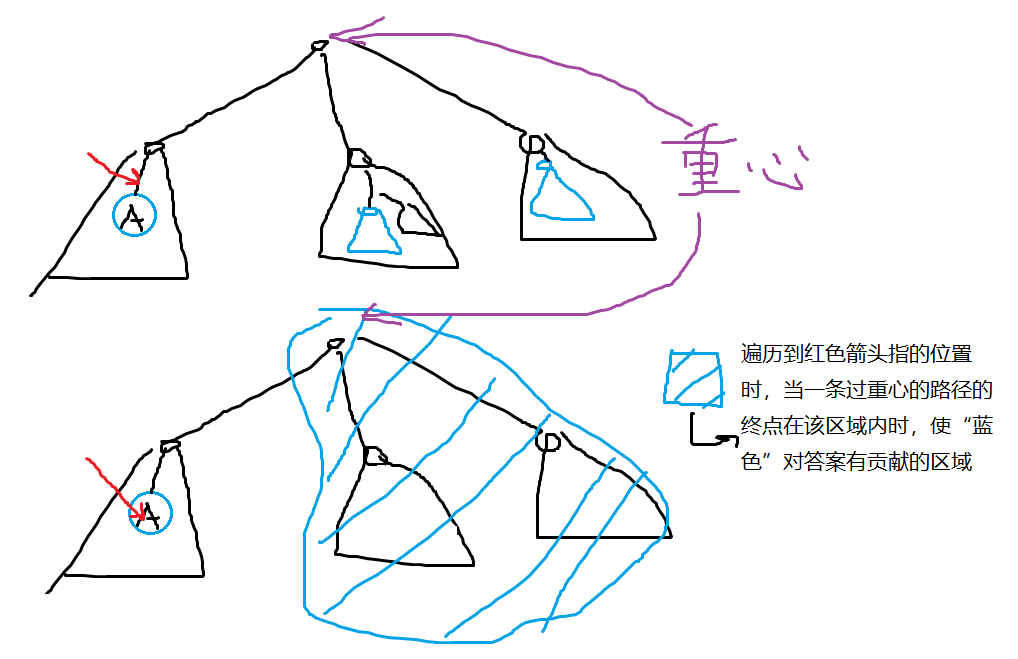
如果当前点(i)的颜色是在重心到它的路径上第一次出现的,(c_i)本来只对终点在大小为(W_{c_i})的区域中的路径有贡献,而现在对所有终点不和(i)在一个重心的儿子的子树里的路径都有贡献
(x+=-(W_{c_i}-w_{c_i})+siz_{重心}-siz_{是当前点祖先的重心的儿子})
画个图说明一下:
代码
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#include<iomanip>
#include<iostream>
#include<map>
#include<queue>
#include<set>
#include<stack>
#include<vector>
#define rep(i,x,y) for(register int i=(x);i<=(y);++i)
#define dwn(i,x,y) for(register int i=(x);i>=(y);--i)
#define maxn 100010
#define LL long long
#define view(u,k) for(int k=fir[u];k!=-1;k=nxt[k])
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)&&ch!='-')ch=getchar();
if(ch=='-')f=-1,ch=getchar();
while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
return x*f;
}
void write(LL x)
{
if(x==0){putchar('0'),putchar('
');return;}
int f=0;char ch[20];
if(x<0)putchar('-'),x=-x;
while(x)ch[++f]=x%10+'0',x/=10;
while(f)putchar(ch[f--]);
putchar('
');
return;
}
int n,c[maxn],fir[maxn],nxt[maxn<<1],v[maxn<<1],siz[maxn],cnt,wt,sumsiz,mnsz,vis[maxn],ext[maxn];
LL sum[maxn],sumall,num[maxn],numnow[maxn],sumnow;
void ade(int u1,int v1){v[cnt]=v1,nxt[cnt]=fir[u1],fir[u1]=cnt++;}
void getwt(int u,int fa)
{
siz[u]=1;int nowmax=0;
view(u,k)if(!vis[v[k]]&&v[k]!=fa)getwt(v[k],u),siz[u]+=siz[v[k]],nowmax=max(nowmax,siz[v[k]]);
if(max(nowmax,sumsiz-siz[u])<mnsz)mnsz=max(nowmax,sumsiz-siz[u]),wt=u;return;
}
void getsz(int u,int fa)
{
siz[u]=1;
view(u,k)if(!vis[v[k]]&&v[k]!=fa)getsz(v[k],u),siz[u]+=siz[v[k]];return;
}
void getc(int u,int fa,int f)
{
int yes=0;
if(!ext[c[u]])ext[c[u]]=1,yes=1;
view(u,k)if(!vis[v[k]]&&v[k]!=fa)getc(v[k],u,f);
if(yes)ext[c[u]]=0,num[c[u]]+=f*siz[u],sumall+=f*siz[u];return;
}
void getnow(int u,int fa,int f)
{
int yes=0;
if(!ext[c[u]])ext[c[u]]=1,yes=1;
view(u,k)if(!vis[v[k]]&&v[k]!=fa)getnow(v[k],u,f);
if(yes)ext[c[u]]=0,numnow[c[u]]+=f*siz[u],sumnow+=f*siz[u];return;
}
void addsum(int u,int fa,LL ad,LL szanc)
{
int yes=0;sum[u]+=ad;
if(!ext[c[u]])yes=1,ext[c[u]]=1,sum[u]+=-(num[c[u]]-numnow[c[u]])+(LL)sumsiz-szanc;
view(u,k)if(!vis[v[k]]&&v[k]!=fa)addsum(v[k],u,yes?ad-(num[c[u]]-numnow[c[u]])+(LL)sumsiz-szanc:ad,szanc);
if(yes)ext[c[u]]=0;
}
void getans(int u,int nowsiz)
{
sumsiz=nowsiz,mnsz=n+1,wt=sumall=0,getwt(u,0);int now=wt;
getsz(now,0),getc(now,0,1);sum[now]+=sumall;ext[c[now]]=1;
view(now,k)if(!vis[v[k]])numnow[c[now]]=siz[v[k]],sumnow=siz[v[k]],getnow(v[k],now,1),addsum(v[k],now,sumall-sumnow,siz[v[k]]),getnow(v[k],now,-1),numnow[c[now]]=0;
ext[c[now]]=0;
getc(now,0,-1); vis[now]=1;
view(now,k)if(!vis[v[k]])getans(v[k],siz[v[k]]);return;
}
int main()
{
n=read();
memset(fir,-1,sizeof(fir));
rep(i,1,n)c[i]=read();
rep(i,1,n-1){int x=read(),y=read();ade(x,y),ade(y,x);}
getans(1,n);
rep(i,1,n)write(sum[i]);
return 0;
}
一些感想
泡狐龙的bgm“妖艶なる舞 〜 タマミツネ”太好听了