并不对劲的后缀数组

后缀数组sa(x)表示排序后第x位在排序前的位置。

这个东西的求法有两种，一种是倍增，时间复杂度o(n log n)或o(n log²n)，另一种是用不知道什么方法做到的o(n)。

至于第二种方法是什么，并不对劲的人并不知道，所以只说倍增。

考虑正常地比较两个字符串，都是从头比较到尾：

 

那么，如果把两个字符串都断成两半，并且已知每一段的排名，就相当于以第一段为第一关键字，第二段为第二关键字排序了。

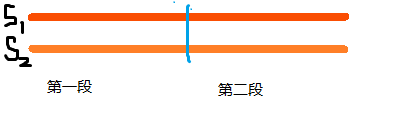
根据这个性质，就能想到如果先把字符串的每个位置开始长度为一的子串进行排序后，就能在至多n log n的时间内将每个位置开始长度为二的子串排序。

↑大概长这样，注意最后要补一个空字符。

以此类推，就能这样倍增地求出后缀的排序了，还是要注意最后补空字符。

如果用基数排序，每次排序的时间复杂度是o(n)的，那么总复杂度就是o(n log n)了。

如果用快速排序，总复杂度就是o(n log²n)，心中有党常数极小才能过。

#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<queue>
#include<stack>
#include<vector>
#define rep(i,x,y) for(register int i=(x);i<=(y);++i)
#define dwn(i,x,y) for(register int i=(x);i>=(y);--i)
#define re register
#define maxn 2000010
using namespace std;
inline int read()
{
    int xx=0,ff=1;
    char ch=getchar();
    while(isdigit(ch)==0&&ch!='-')ch=getchar();
    if(ch=='-')ff=-1,ch=getchar();
    while(isdigit(ch))xx=xx*10+ch-'0',ch=getchar();
    return xx*ff;
}
void write(int x)
{
    int ff=0;char ch[15];
    if(x<0)
    {
        x=-x;
        putchar('-');
    }
    while(x)ch[++ff]=(x%10)+'0',x/=10;
    if(ff==0)putchar('0');
    while(ff)putchar(ch[ff--]);
    putchar(' ');
}   
int sa[maxn],ord[maxn],rnk[maxn],n,m; 
int sum[maxn];
char s[maxn];
int main()
{
    scanf("%s",s+1);
    n=strlen(s+1);m=130;
    rep(i,1,n)sum[rnk[i]=s[i]]++;
    rep(i,1,m)sum[i]+=sum[i-1];
    dwn(i,n,1)sa[sum[rnk[i]]--]=i;
    for (int k=1;k<=n;k<<=1) 
    { 
        //从这里开始到分界线是更新sa的部分 
        int p=0;
        rep(i,n-k+1,n)ord[++p]=i;
        rep(i,1,n)if(sa[i]>=k+1)ord[++p]=sa[i]-k;
        //ord[i]表示按第二关键字排名后排在第i位的在原串中的位置
        //需要注意的是，原串中的第n-k+1到n位置上的后缀由于加上k后的位置在超过n的地方，需要补空字符
        //这里假设空字符是最小的，所以按第二关键字排序后，第n-k+1到n位置上的后缀排在最前面 
        rep(i,0,m)sum[i]=0;
        rep(i,1,n)sum[rnk[i]]++;//计算不同的排名出现了多少次 
        rep(i,1,m)sum[i]+=sum[i-1];//算前缀和。c[i]表示排名为i的串最后一次出现在排序后的第几名（当k<n时可能在s中有很多个排名相同的） 
        dwn(i,n,1)sa[sum[rnk[ord[i]]]--]=ord[i];//rnk[ord[i]]表示排序后第i个的排名（可能会重）是多少 
        //不能直接写sa[sum[rnk[i]]--]=i
		//交换前，x[i]表示从i开始的后缀在上一轮的排名
        //——————————分界线————————————
        //从这里开始是更新x的部分 
        swap(rnk,ord);
        p=1,rnk[sa[1]]=1;
        rep(i,2,n)rnk[sa[i]]=(ord[sa[i-1]]==ord[sa[i]]&&ord[sa[i-1]+k]==ord[sa[i]+k])?p:++p;
        if(p>=n)break;
        m=p;
    }
    rep(i,1,n)write(sa[i]);
    return 0;
}