顾名思义,就是对于每次操作,将用新的节点替代本应修改的节点。由于每次单点修改只会改log n个节点,所以动态开点可以做到空间是q log n + n的。
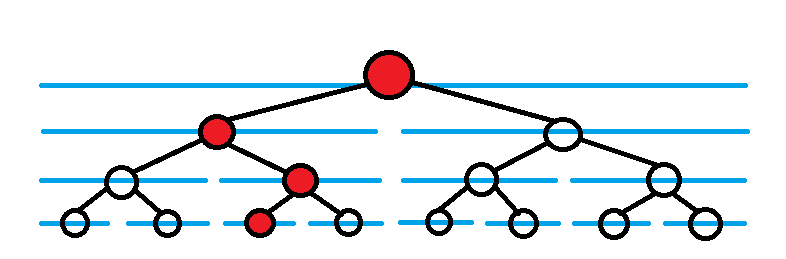
这是一棵对劲的线段树,要修改这一串红色的点。普通的线段树是直接修改。

对于可持久化线段树而言,则是新建一些节点,替换掉应该修改的节点。原来的节点不做任何改动。
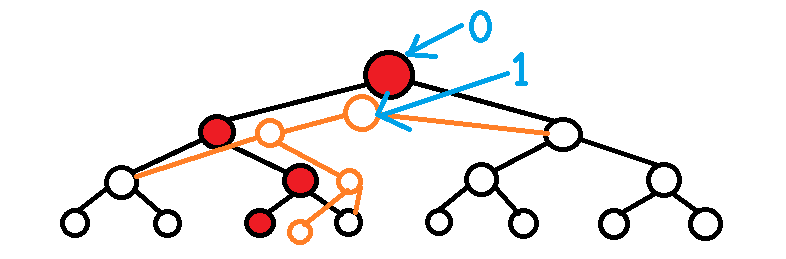
记得存根的版本指针。
这样就可以实现带撤销操作的线段树了!但是这并不是它的主要优势。它的主要优势在于可以实现主席树(人称Mr.Jiang‘s tree)。
主席树能查询静态区间第k大。再套上树状数组就能维护动态区间第k大。先考虑静态区间第k大。
将原数列离散化后,开一棵值域可持久化线段树。按从左到右的顺序插入每一个数。这样,第x个版本的线段树就代表数列中从1到x离散化后在一段取值范围内的出现情况。第0个版本就是一个数都没有。
查询l到r第k大时,就可以用前缀和的思想,用第r个版本的线段树减去第l-1个。这样得到的线段树就是表示某段取值范围中,在数列中在l-r中的数的个数。当左边的个数大于k时就走左边,否则走右边。需要注意的是,当总共的个数都小于k时,就无解了。

#include<iostream> #include<iomanip> #include<cstdio> #include<cstring> #include<cstdlib> #include<cmath> #include<algorithm> #define maxn 200010 using namespace std; int read() { int f=1,x=0;char ch=getchar(); while(isdigit(ch)==0 && ch!='-')ch=getchar(); if(ch=='-')f=-1,ch=getchar(); while(isdigit(ch))x=x*10+ch-'0',ch=getchar(); return x*f; } void write(int x) { int ff=0;char ch[15]; if(x<0) { x=-x; putchar('-'); } while(x)ch[++ff]=(x%10)+'0',x/=10; if(ff==0)putchar('0'); while(ff)putchar(ch[ff--]); putchar(' '); } typedef struct node { int key,lson,rson; }tree; tree x[maxn*30]; int n,rt[maxn],a[maxn],cnt,ord[maxn],rnk[maxn],t; void build(int li,int ri,int node) { x[node].key=0; if(li==ri) { x[node].lson=x[node].rson=0; return; } int mid=(li+ri)>>1; x[node].lson=++cnt; build(li,mid,cnt); x[node].rson=++cnt; build(mid+1,ri,cnt); } int add(int li,int ri,int pla,int k,int node) { if(ri<pla || li>pla)return node; if(li==pla&&ri==pla) { x[++cnt].key=k; return cnt; } int mid=(li+ri)>>1; int lnew=add(li,mid,pla,k,x[node].lson); int rnew=add(mid+1,ri,pla,k,x[node].rson); int tmp=x[lnew].key+x[rnew].key; if(tmp!=x[node].key) { node=++cnt; x[node].lson=lnew,x[node].rson=rnew; x[node].key=tmp; } return node; } bool cmp(int xx,int yy) { return a[xx]<a[yy]; } int query(int node1,int node2,int li,int ri,int k) { int mid=(li+ri)>>1; if (li==ri) { // cout<<"Shing Zhing Gay"<<endl; return li; } // cout<<node1<<" "<<node2<<" "<<x[node1].key<<" "<<x[node2].key<<endl; if (x[x[node2].lson].key-x[x[node1].lson].key>=k) return query(x[node1].lson,x[node2].lson,li,mid,k); else if (x[node2].key-x[node1].key>=k) return query(x[node1].rson,x[node2].rson,mid+1,ri,k-(x[x[node2].lson].key-x[x[node1].lson].key)); else return 0; } void ask() { int l=read(),r=read(),k=read(); int tmp=query(rt[l-1],rt[r],1,n,k); write(a[ord[tmp]]); } void work() { n=read(),t=read(); for(int i=1;i<=n;i++) a[i]=read(),ord[i]=i; rt[0]=cnt=1; sort(ord+1,ord+n+1,cmp); build(1,n,1); for(int i=1;i<=n;i++) rnk[ord[i]]=i; for(int i=1;i<=n;i++) { rt[i]=add(1,n,rnk[i],1,rt[i-1]); } while(t--) ask(); } int main() { work(); return 0; } /* 5 5 25957 6405 15770 26287 26465 2 2 1 3 4 1 4 5 1 1 2 2 4 4 1 */
gdc没有手
