在上一文中介绍了碰撞查询的配置方法:
本篇介绍下UE4的各种零大小的射线检测,以及非零大小(带体积)的射线检测(如球,胶囊体,盒子),对应于PhysX的Raycast和Sweep。
先看下演示实例:

UE4总共支持四种类型的Trace,从外到里依次是LineTrace,SphereTrace,CapsuleTrace和BoxTrace,性能代价也是依次增加的。除了SingleLineTrace的版本,还有相应的MultiLineTrace,两者区别仅仅在于碰到阻挡后是否会继续检测下去,也就体现在蓝图结点的输出上,一个是单结构体,另一个是数组。
简单说下演示的蓝图实现:
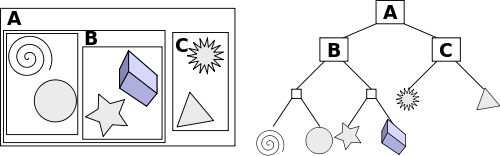
新建一个蓝图类,继承自Actor,然后在这里添加两个staticmesh组件,将方形mesh作为根组件(拖到默认的SceneComponet上面),将圆形mesh组件Attach到方mesh上,并手动调整位置即可,如下:
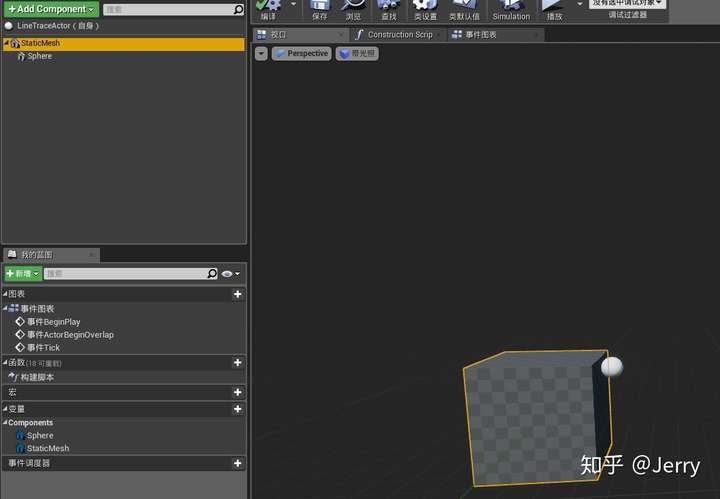
再在事件图表里面这样配置即可:
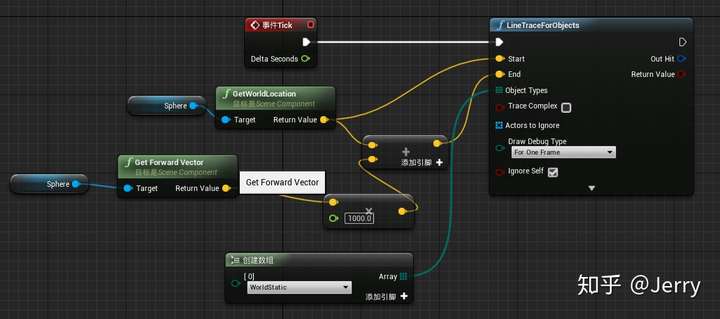
注意要在LineTraceForObjects结点上打开DrawDebugType才可以看到打出的射线,默认红色线段表示未碰撞,绿色表示碰撞(这点与人的自然理解相反,要区分下)。
有体积碰撞是类似的,只在trace结点上不同,以CapsuleTrace为例,如下:
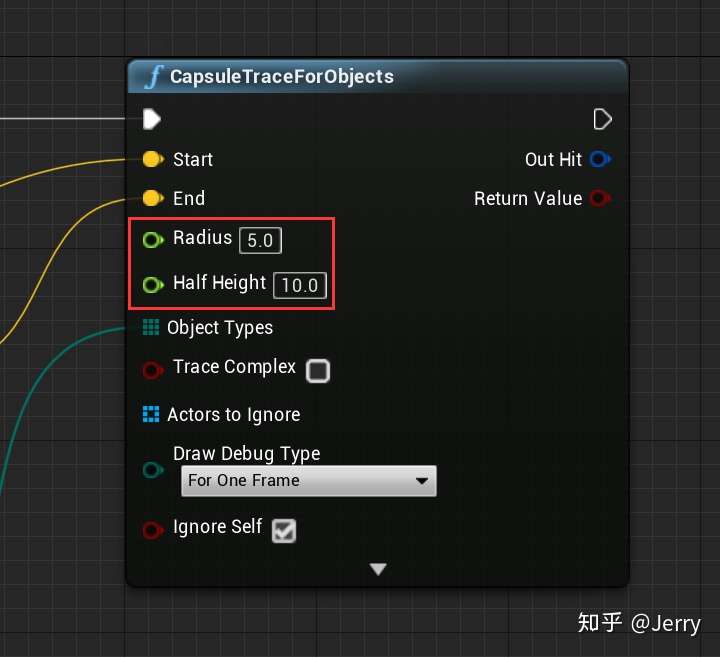
只要填写多出来的参数就行了,这里是配置Capsule的前端半球半径与柱子半高,其他类似。会使用射线检测是一方面,还应知其然知其所以然,下面来介绍下常用的碰撞检测算法。
前篇已经说了碰撞是一对物体相互作用才有意义,暴力查询碰撞方法是两两遍历,也就是O(N^2)的时间复杂度,N是场景对象数量,对于大世界万级起步的对象数量而言,这种Brute-force算法简直是灾难。
所以不仅仅是PhysX,其他有名的物理引擎也会将碰撞查询细分成三个阶段,即:
- Broad Phase
- Mid Phase
- Narrow Phase
其实可以也会将Mid Phase划规到Broad Phase来,目的都是利用空间相关性,过滤掉空间相差太远而不可能发生碰撞的对象。在BroadPhase和MidPhase中都是使用物理的AABB包围盒来进行计算的,包围盒的每条边都与相应XYZ轴平行。本篇重点介绍BroadPhase/MidPhase中常用的SAP算法、MBP算法与AABB树(BVH)算法。
在讲具体的算法前,有一个地方是明确的,如下图(截图取自文末附的链接):
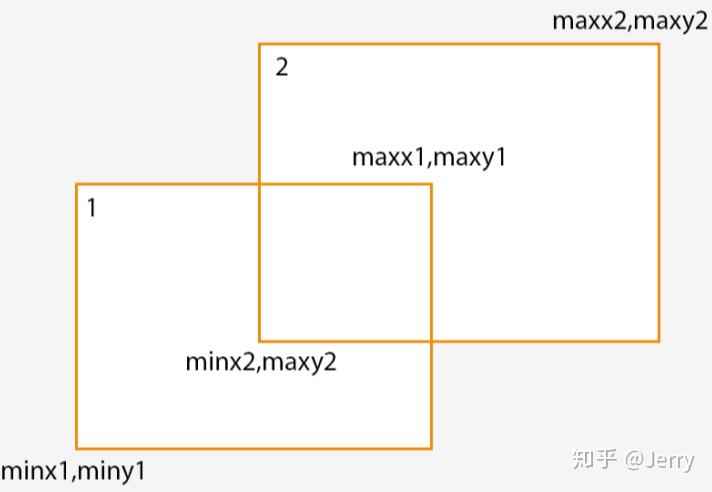
任何包围盒可以用它在空间中左下的点Min和右上的点Max来描述,为了简化起见,后面都用2D图示说明,上图1号包围盒的Min点表示成(MinX1, MinY1),Max点表示成(MaxX1, MaxY1),同理2号包围盒的Min点是(MinX2, MinY2),Max点为(MaxX2, MaxY2),那么两个包围盒重合的充分必要条件是:
MaxX1 > MinX2 && MinX1 < MaxX2 && MaxY1 > MinY2 && MinY1 < MaxY2
可以简化成“两物体碰撞的充分必要条件是在所有轴向上的各自最大值点要大于另一方最小值点”。
SAP算法
PhysX在Broad Phase中采用的是一种称之为Sweep And Prune(SAP)算法,它将所有物体AABB盒的Min点与Max点分别在XYZ轴上投影,如果在某一轴上不满足Max1 > Min2 && Max2 > Min1则不会发生碰撞。
具体见下图示(以在横轴X方向上的投影为例):
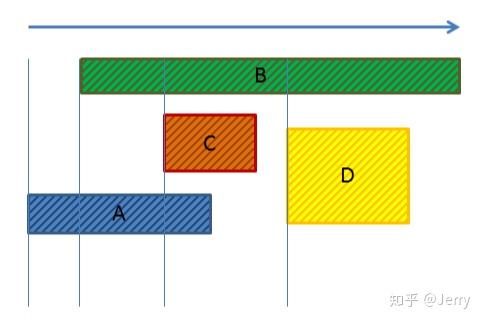
第一步:排序
对ABCD四个图形按最小点排序,由小到大(由左及右)的顺序分别是A,B,C,D
第二步:建立碰撞可能性列表List_X
对每个对象进行遍历,先是A,按之前排序的顺序往下检测:
检测B,发现AB满足最大点大于最小点的充要条件,则将{A,B}加入List_X中
检测C,发现AC也满足最大点大于最小点,则将{A,C}加入List_X中
检测D,发现A的最大点小于了D的最小点,不加入List中,因为是事先排过序的,所以D之后的物体不再检测
然后回到外层循环,同理对B,C,D分别处理
得到可能性列表List_X={A,B}, {A,C}, {B,C}, {B,D}。
第三步:对其他轴向进行检测,得到List_Y, List_Z,只有同时位于三个列表中的pair才是可能的碰撞对。
但第三步这里对空间存储的要求比较大,需要存储三个列表,每个列表中也会包含大量元素pair,所以另一种可取的方案,是在List_X的基础上进行Y和Z轴的校验,不通过就直接从List_X中排除,这样只用一个列表的空间就能搞定。
有些同学可能会对第二步质疑,内外两循环看上去仍是O(N^2)的复杂度,但因为有了第一步排序,可以快速排掉不满足条件的后面所有碰撞体,所以平均复杂度是降低了,加上排序的平均时间复杂度,SAP算法的平均复杂度是O(nlogn)。
MBP算法
SAP对于大量静态物体的场景效果很好,但对于运动的对象,需要进行增量更新,如下图:
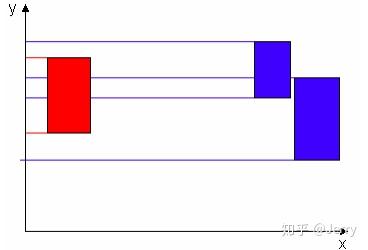
红色运动物体在Y轴方向运动,尽管它们在X轴上相差很远,但传统SAP还是不得不更新它在Y轴上的信息。为了进一步利用空间相关性解决上述问题,不少SAP的改进算法,如Multi-SAP,Multi Box Pruning(简称MBP)等将世界划分成网格,如下:

在每一个网格中进行局部的SAP,辅以并行计算的技术,要比SAP更快,代码可以参见:
www.codercorner.com/BoxPruning.zip
在PhysX 3.3版时,引入MBP算法如下:
第一步:计算所有对象的整体包围盒,下图圆圈表示物体,外层黑框是它的整体大包围盒。
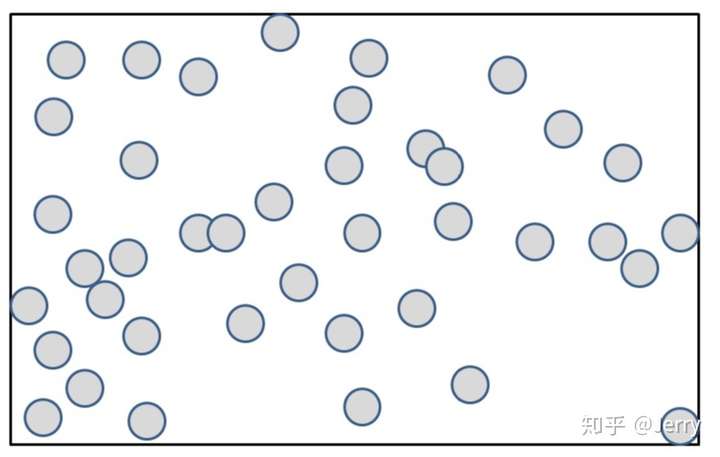
第二步:切分这个包围盒,划规成四个子计算区间。
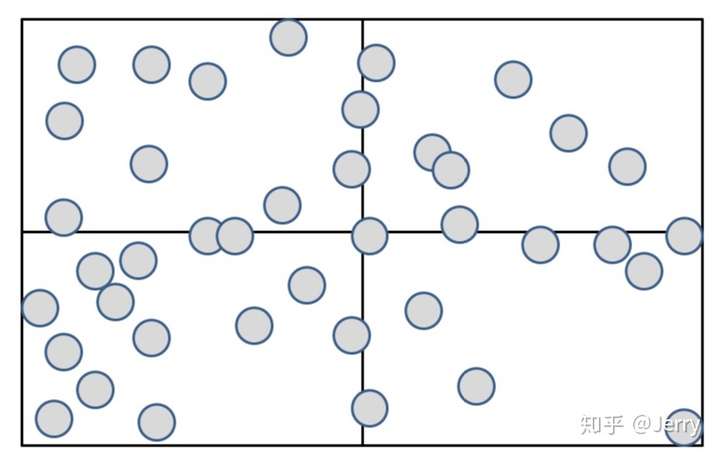
第三步:按各自区域进行分类,如下:
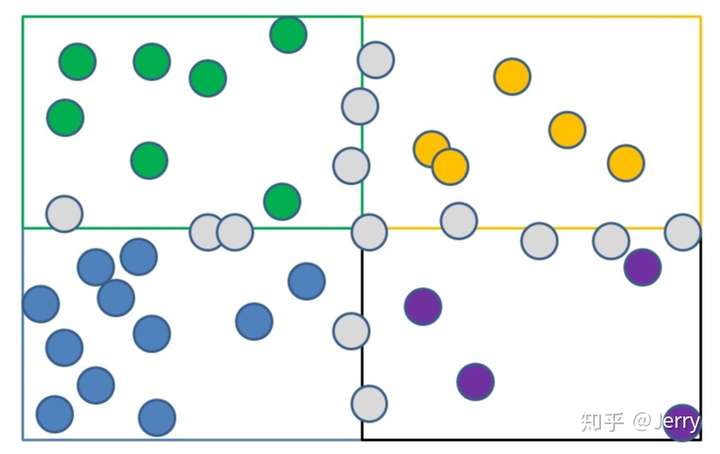
每个颜色表示各自的归属。
第四步:考虑轴线上的物体的归属,因落入了两个或两个以上的区域,所以这些区域内都需要添加。在实际计算过程中,轴线左侧两个小红球,它们在绿色区域内会检测到碰撞,同时在蓝色区域内也会检测到碰撞,但如果碰撞列表用hashmap来做,就不用担心重复性。
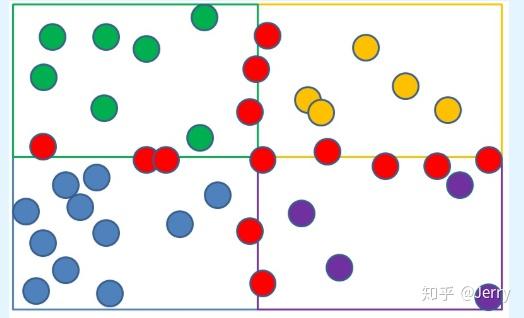
第五步:对每一个区域递归地进行划分,比如左上绿色区域再划成四块,直到区域足够小为止。
之后在每个小区域内进行经典SAP的计算,就可以了。
对比下经典SAP与MBP算法,可以看到MBP的优点在于计算更快,特别是大量动态对象的碰撞计算,缺点就是需要有“网格”的概念,即需要知道世界边界;SAP则不需要边界信息,对静态对象碰撞计算更友好。
BVH算法
除以之外,还有一种AABB树或Bounding Volume Hierarchical Tree(BVH)树,也可用于BroadPhase/MidPhase的计算。
在介绍AABB树时,要事先定义两个概念:
Branch:AABB树都是完全二叉的,所以每个分支有两个Child结点或者没有结点,Branch有一个逻辑上的AABB盒,必须包含它的Child的AABB。
Leaf:叶结点包含了实际的物理对象,也被描述成AABB。
Root:根结点可以是Branch或者是Leaf(当只有一个物理对象时)
AABB树的算法分为建树、查树、更新树三个大部分,分别介绍:
建树
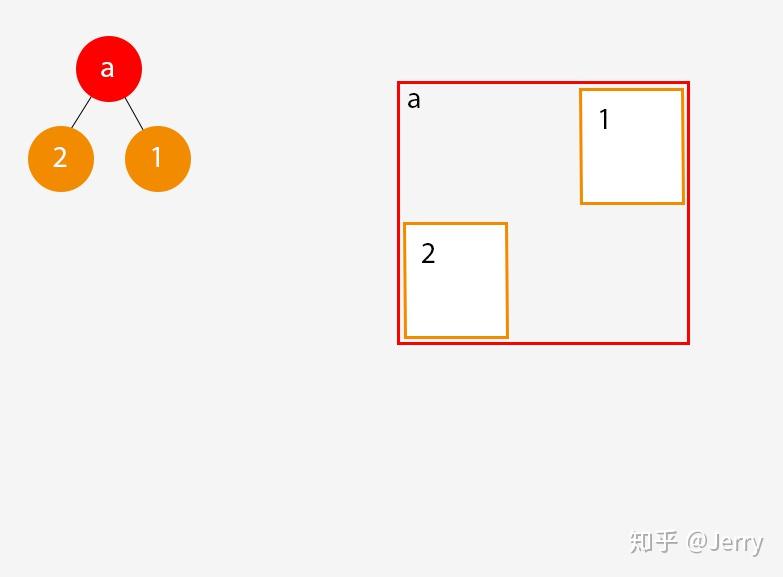
将第一个Object添加到空场景时,Root就是一个Leaf结点:
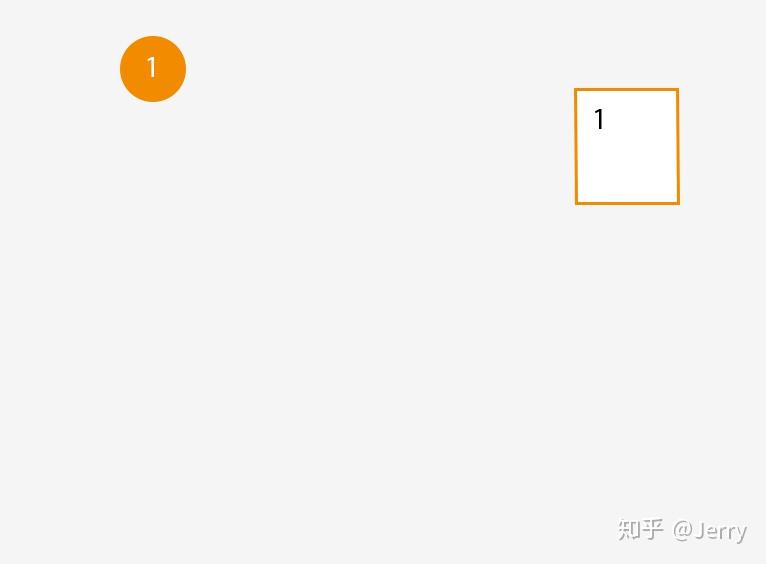
添加第二个Object时,我们会新建一个Branch给Root,然后把Object1和Object2加入到它的Leaf结点中,结果如下:
再增加一个Object3,此时结果如下:
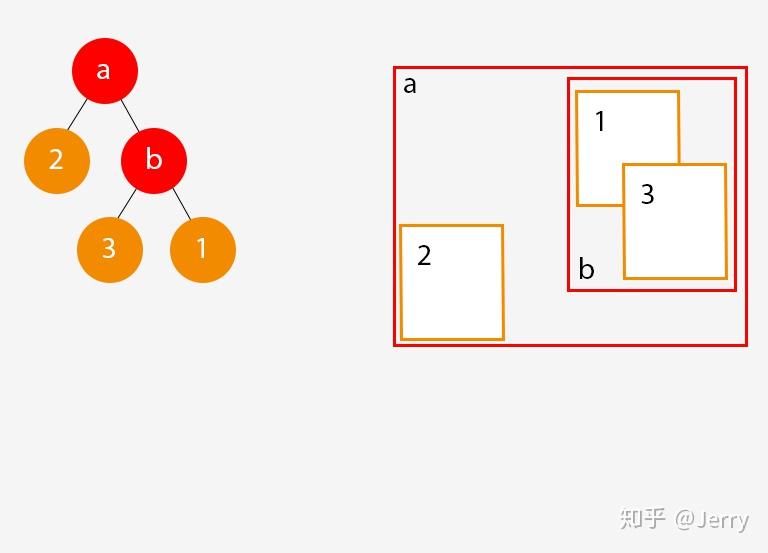
经历的步骤细化如下:
(1)创建新的分支结点b,赋给它一个逻辑上的AABB,以使它可以包围Object1和Object3;
(2)将新加的Object3赋给b的分支的子结点leaf3;
(3)将第二步里面的leaf1移至b分支的子结点leaf1;
(4)将branch b赋给第二步中leaf1所在的位置;
(5)调整branch a的逻辑AABB,以使它可以包围住leaf2和branch b的AABB;
将以上步骤概括一下得到每加一个Object的通用算法:
- 为新Object创建一个leaf node,leaf node的AABB盒可以包住这个Object;
- 为第1步中的leaf node找到一个合适的邻居(可能是branch,也可能是leaf);
- 建立一个新的branch,它的AABB要包住第2步中的邻居结点和第1步中的新结点;
- 将第1步中的新结点加到第3步的branch的子结点上;
- 将第2步中的邻居从老树中删除,并加到第3步的branch的子结点上;
- 将第3步的branch添加到树上,位置就是第2步的邻居位置;
- 更新树中所有branch的AABB,以使其可以包围住它所有子结点的AABB;
那么何为第2步中的"合适"结点,一般来说调整的代价越低,调整后的树越平衡,就越合适,在实际计算中,可以为每次调整定义一个花费,花费值算下来最小的方案是最佳的调整方案。
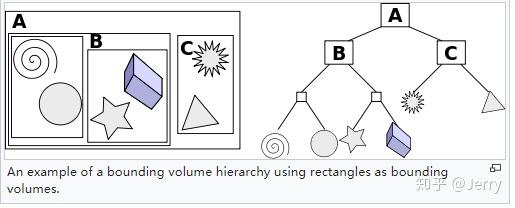
摘取wiki一个很好的示意图:
查树
在计算碰撞时,就需要用到查树的算法了,如下:
- 从根结点开始遍历,检测当前结点AABB是否与待测对象相交
- 如果相交,并且树上结点是一个leaf node,则将结点对象与待测对象加入到列表中
- 如果相交,并且树上结点是一个branch node,则递归到它的左子树和右子树,重复上述过程
最终会得到一个与待测对象潜在碰撞的对象列表,之后再跑narrow phase来决定最终碰撞。上述算法可以递归实现,但推荐采用用栈来实现递归,如下:
- 将root node加入栈中
- 如果栈非空,那么
(a)弹出栈顶node
(b)检测此node的AABB是否与待测对象的AABB相交
(c)如果相交,则
(i)如果它是一个leaf node,则将此leaf node加入到潜在碰撞列表中
(ii)如果它是一个branch node,则将它的左子树和右子树分别push到栈顶,重复上述过程
用图片演示一下这个过程,建立的AABB树如下:
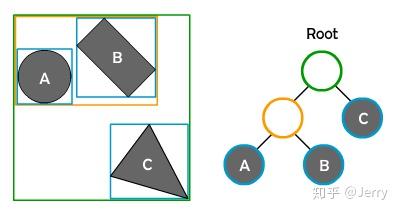
要检测一条射线行进过程中打中的对象,如下图红线:
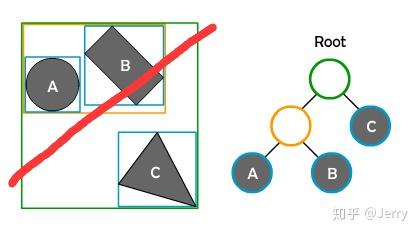
先从root开始,发现红线的AABB与root有重合,如下图所示:
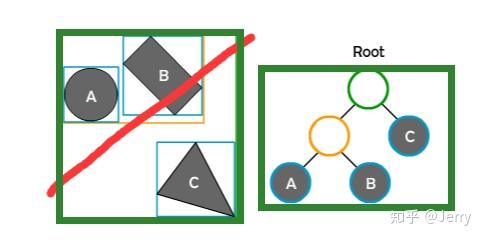
那么栈上就有了它的左子树NodeAB与右子树NodeC,这时检测与左子树NodeAB的AABB盒的相交性,是相交的,继续把NodeAB的左子树nodeA与右子树nodeB加入到栈顶,如下:
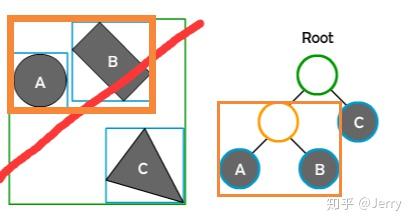
判断nodeA包围盒与射线的相交性,是不相交的,则不做处理;再判断nodeB与射线的相交性,是相交的,且nodeB是一个leaf node,所以将之加入到碰撞列表中,如下:
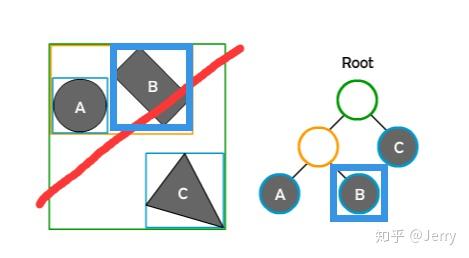
此时栈中仅剩下nodeC,弹出之,检测相交性是不相交的,故不做操作。再看栈已经是空的了,那么查树的操作就结束,返回碰撞列表{B}。
更新树
对于动态对象而言,它的位置、旋转、绽放等会影响AABB,因此需要动态更新。但根据帧间的相关性,即使是动态对象,每帧AABB发生的变化其实不大,而且本身作为broadphase/midphase阶段,如果适当放大AABB有助于减少每次更新量并且不会影响最终结果的正确性。
比如按移动方向来适当放大("fatten")物体的AABB,如下:
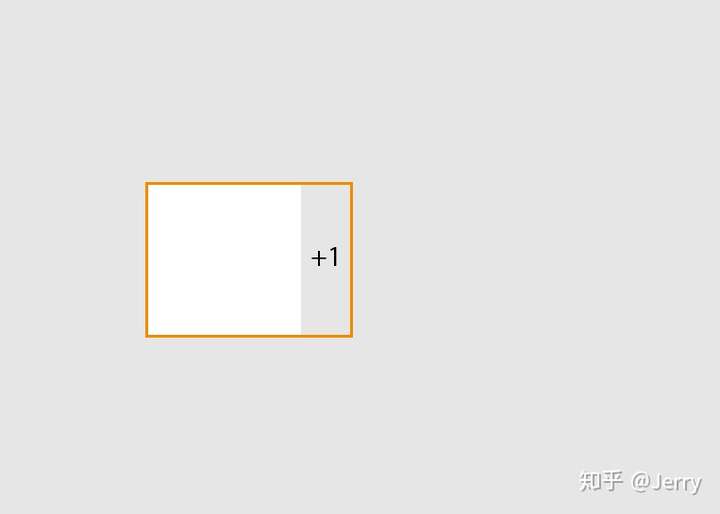
以上就是broadphase/midphase阶段常用的SAP、MBP和AABB树(BVH)算法,参考链接附上如下(可能需要kexue上网):
https://github.com/mattleibow/jitterphysics/wiki/Sweep-and-Prunehttp://www.codercorner.com/blog/?p=1978Bounding volume hierarchy
Introductory Guide to AABB Tree Collision Detection
http://allenchou.net/2014/02/game-physics-broadphase-dynamic-aabb-tree/
现在UE4自己chaos的算法还没有研究(要等4.23才有完整版),无论怎么做,算法应该是类似的。