Div2
A
长度为(n(n≤10^5))的数组,每个元素不同,求有多少个位置(d)满足(d - x le j < d And d < j le d + y a_d<a_j(0le x,yle 7))
(x,y)较小,遍历每个位置,暴力判断即可
B
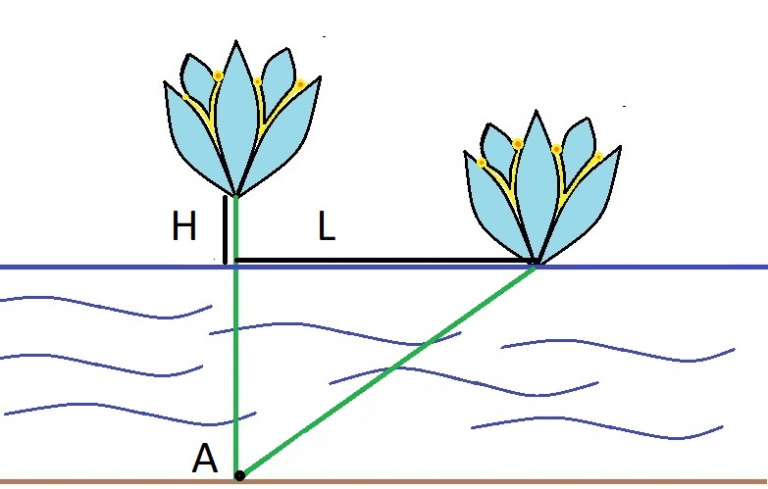
如下图,给出(L,H),求水面深度
设水面深度为(x),勾股定理:(x^2+L^2=(x+H)^2),解得(x=frac{L^2-H^2}{2H})
Div1
A
长度为(n(1 le n le 4 cdot 10^{5}))的数组和(I(1 le I le 10^{8})),确定一个范围([L,R]),使得该范围内数组的元素个数(K)((满足)lceil log_{2} K ceilcdot n≤8I)$。求不在此范围内的元素最少为多少
得出最大(K),将原数组排序去重离散得到一个排列及每个数字出现的次数
转换为:(1~ tot)的数字,给出每个数字出现的次数,选连续(K)个数字,求未选中数字的最小个数
判断选择([1,K],[2,K+1],[n-K+1,n]),没被选中的数字至多为首尾连续两段,预处理前缀和和后缀和暴力判断即可
B
长度为(n)的数组,和(q)次操作
两种操作(1.a_x=p),(2.)数组里小于(x)的全部修改为(x)
有没有写平衡树的呀
单独考虑(a_x),第一种操作的影响为最后一次修改(x)位置的值(p),第二种操作的影响为最后一次操作一后的每次操作
统计每个(x)最后一次操作一的位置,并对第二种操作统计最大后缀,最后取(max)
C
(3cdot n)个点(m)条边,选出(n)大小的独立点集或独立边集(1 leq n leq 10^{5},0 leq m leq 5 cdot 10^{5})
随便选边,设独立边集为(len)
-
(len≥n):输出边集
-
(len<n):输出没在边集里的大小为(n)的点集(()点集的最大大小为(3cdot n-2(n-1)≥n))
D
(n×n(1 leq n leq 50))的黑白色格子,将一块长(h)宽(w)的范围涂白,花费(max(h,w)),求全涂白的最小花费
普及组的暴力?(f_{x,y,xx,yy})为将((x,y)(xx,yy))范围全涂白的最小花费,记忆化搜索即可