用Java实现一个二叉树

介绍

使用Java实现一个int值类型的排序二叉树

二叉树

二叉树是一个递归的数据结构，每个节点最多有两个子节点。
通常二叉树是二分查找树，每个节点它的值大于或者等于在它左子树节点上的值，小于或者等于在它右子树节点上的值，如下图

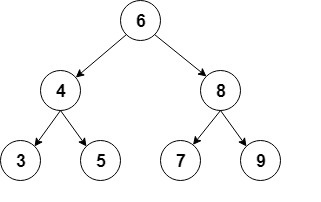
为了实现二叉树，我们使用一个Node类来表示节点，节点存储int类型的值，还有对子节点的引用。

package com.java.node.BinaryTree;
public class Node {
    int data;
    Node left;
    Node right;
    public Node(int data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

然后添加树的root节点

package com.java.node.BinaryTree;
public class BinaryTree {
    Node root;
}

通常的操作

添加节点

首先我们必须找到新节点的位置，是为了保持树排序。我们必须从root节点开始，必须遵循下面的规则：

• 如果新节点小于当前的值，我们将会进入左子树
• 如果新节点大于当前的节点。我们将会进入右子树
• 当当前的节点是null时，我们已经到达叶子节点，我们可以添加新节点到这个位置。
  我们将会创建递归方法做添加节点操作

    private Node addNode(Node current, int value) {
        if (current == null) {
            return new Node(value);
        }
        if (value < current.data) {
            current.left = addNode(current.left, value);
        } else if (value > current.data) {
            current.right = addNode(current.right, value);
        } else {
            return current;
        }
        return current;
    }
    public void addNode(int value) {
        root = addNode(root, value);
    }

可以使用方法创建一个二叉树了

public BinaryTree createBinaryTree() {
        BinaryTree bt = new BinaryTree();
        bt.addNode(6);
        bt.addNode(4);
        bt.addNode(8);
        bt.addNode(10);
        return bt;
    }

查找一个节点

    private boolean containNode(Node current, int value) {
        if (current == null) {
            return false;
        }
        if (value == current.data) {
            return true;
        }
        return value < current.data ? containNode(current.left, value) : containNode(current.right, value);
    }
    public boolean containNode(int value) {
        return containNode(root, value);
    }

删除一个节点

private Node deleteNode(Node current, int value) {
        if (current == null) {
            return null;
        }
        if (value == current.data) {
            if (current.left == null && current.right == null) {
                return null;
            }
            if (current.left == null) {
                return current.right;
            }
            if (current.right == null) {
                return current.left;
            }
            int smallestValue = findSmallestValue(current.right);
            current.data = smallestValue;
            current.right = deleteNode(current.right, smallestValue);
            return current;
        }
        if (value < current.data) {
            current.left = deleteNode(current.left, value);
            return current;
        }
        current.right = deleteNode(current.right, value);
        return current;
    }
    private int findSmallestValue(Node root) {
        return root.left == null ? root.data : findSmallestValue(root.right);
    }

遍历树

我们将以不同的方式遍历树，以depth-first，breadth-first方式遍历树。
以Depth-First遍历树
Depth-first查询是一种在查询兄弟节点之前，尽可能的查询每个子节点。
in-order，pre-order，post-order方式都是以depth-first方式遍历树的。

in-order遍历是首先遍历左子树，然后root节点，最后是右子树。

    public void traverseInOrder(Node root) {
        if (root != null) {
            traverseInOrder(root.left);
            System.out.println(root.data);
            traverseInOrder(root.right);
        }
    }

pre-order遍历首先是root节点，然后是左子树，最后是右子树。

public void traversePreOrder(Node root) {
        if (root != null) {
            System.out.println(root.data);
            traversePreOrder(root.left);
            traversePreOrder(root.right);
        }
    }

post-order遍历首先是遍历左子树，然后是右子树，最后是root节点。

public void traversePostOrder(Node root) {
        if (root != null) {
            traversePostOrder(root.left);
            traversePostOrder(root.right);
            System.out.println(root.data);
        }
    }

以Breadth-First遍历
它在遍历下一级的节点之前，会遍历当前级的所有节点。
这种类型的遍历也叫做level-order，遍历树从root节点开始，从左到右。
为了实现，使用队列来存储每个级别的节点。我们将会从列表中获取每个节点。然后添加他的子节点到队列中。

public void traverseLevelOrder(Node root) {
        if (root == null) {
            return;
        }
        Queue<Node> nodes = new LinkedList<Node>();
        nodes.add(root);
        while(!nodes.isEmpty()) {
            Node node = nodes.remove();
            System.out.println(node.data);
            if (node.left != null) {
                nodes.add(node.left);
            }
						
            if (node.right != null) {
                nodes.add(node.right);
            }
        }
    }