线性回归
若只考虑两个特征变量我们可以建立线性方程：
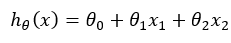
对于多个特征变量我们可以建立：
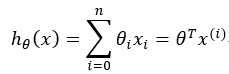
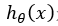是预测值，它与真实值存在一定的误差：
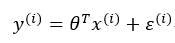
为预测值，y(i)为真实值。
误差ε(i)是独立同分布的，服从均值为0，方差为某定值σ2的高斯分布
为什么每个样本误差ε是独立同分布的？
答：误差可能是正的也可能是负的，它们之间是独立的互不影响，每个样本都是独立的。误差分布情况是独立的，进行的任务都是同一个任务，同一个任务带来的分布都是同分布的。服从中心极限定理，指的是随机变量x之间独立同分布，那么这些变量求和就服从正态分布。预测值有比样本误差大，有比样本误差小的。这样有多，有少，均值为0。
实际问题中，很多随机现象可以看作众多因素的独立影响的综合反应，往往近似服从正态分布：
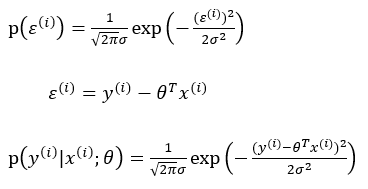
为了是预测值与真实值尽可能的接近，即误差尽可能小，所以尽可能大，将所有的样本的正态分布组合起来，得到似然函数：
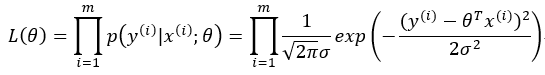
为求得最大似然估计，我们先对似然函数取对数
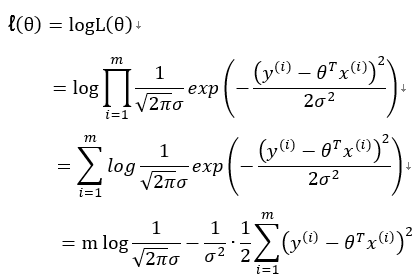
要求解对数似然函数最大值可以通过求解J(θ)的最小值来求得。
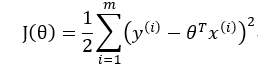
上式中我们对θ偏导
1）首先通过θ的解析式求解：
将M个N维样本组成矩阵X：
X的每一行对应一个样本，共M个样本
X的每一列对应样本的一个维度，共N维
还有额外的一维常数项，全为1
从而XTX+λI可逆，保证回归公式一定有意义。
对目标函数J(θ)还可以加正则项来防止过拟合，同时正则项的加入可以提高多项式高阶的系数的稳定性，也就是说，它可以使高阶项的系数向0靠近，避免出现几百几千甚至更高的系数，从而使得多项式更加稳定。在一定程度上减小了噪音点的影响。
L2正则即Ridge（岭回归）
L1正则即LASSO回归
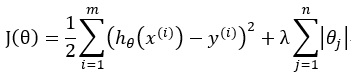
将L1与L2结合的正则项 λ>0, ρ∈[0,1]
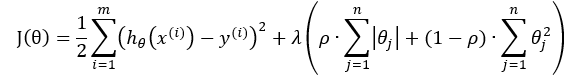
对于L1正则项如何处理梯度？
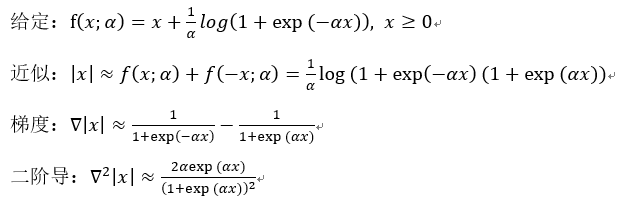
2）梯度下降算法
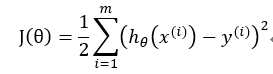
随机初始化θ，沿着负梯度方向迭代，更新后的θ使J(θ)更小
α：学习率、步长
上式是对第j个参数θj求偏导所以其它的元素均看作常量只有xjθj有效，所以
对θj的偏导为xj
因此更新θj
这里的x(i)指的是一个样本点的不同特征，相当于一组数据集的行
比如X表示一朵花，那可以用 x1,x2,x3,x4… 分别表示：花瓣的颜色，花瓣数目，花瓣的长，花瓣的宽…，对于每一个样本X我们都使用参数θ
梯度下降算法有三种BGD、SGD、MBGD
转自https://blog.csdn.net/kwame211/article/details/80364079
BGD(Batch gradient descent)批量梯度下降法：每次迭代使用所有的样本
每次迭代都需要把所有样本都送入，这样的好处是每次迭代都顾及了全部的样本，做的是全局最优化
SGD（Stochastic gradientdescent）随机梯度下降法：每次迭代使用一组样本
针对BGD算法训练速度过慢的缺点，提出了SGD算法，普通的BGD算法是每次迭代把所有样本都过一遍，每训练一组样本就把梯度更新一次。而SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。
MBGD（Mini-batch gradient descent）小批量梯度下降：每次迭代使用b组样本
SGD相对来说要快很多，但是也有存在问题，由于单个样本的训练可能会带来很多噪声，使得SGD并不是每次迭代都向着整体最优化方向，因此在刚开始训练时可能收敛得很快，但是训练一段时间后就会变得很慢。在此基础上又提出了小批量梯度下降法，它是每次从样本中随机抽取一小批进行训练，而不是一组。