面试常见高频算法题总结

一、链表相关

1.链表反转

class Solution {
    public ListNode reverseList(ListNode head) {
        // base case
        if(head == null || head.next == null) return head;  
        
        ListNode first = head;
        ListNode result = null;//建立一个新的节点用来存放结果
        ListNode second = null;
        while(first != null){ //遍历输入链表，开始处理每一个节点
            second = first.next;  //先处理第一个节点first，所以需要一个指针来存储first的后继
            first.next = result; //将first放到新链表头节点的头部
            result = first; //移动新链表的头指针，让它始终指向新链表头部
            first = second; //继续处理原链表的节点，即之前指针存放的后继，循环往复
        }
        return result;
    }
}

 2.k个一组翻转链表(力扣 25) --------比较难

3.判断链表是否有环

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
   public boolean hasCycle(ListNode head) {//设置快慢指针，若有环一定会在环里面相遇。否则会有null值
    if(head==null) return false;
    ListNode walker = head;
    ListNode runner = head;
    while(runner.next!=null && runner.next.next!=null) {
        walker = walker.next;
        runner = runner.next.next;
        if(walker==runner) return true;
    }
    return false;
  }
}

//也可以采用hashmap把每一个节点存储起来，如果地址相同则存在节点 

二、数组、字符串巧妙解法相关

1.不使用除法实现除自身外数组元素的乘积（力扣 238）

public class Solution {
    
   public int[] productExceptSelf(int[] nums) {
       int n = nums.length;
       int[] res = new int[n];
       res[0] = 1;
       for (int i = 1; i < n; i++) {
          res[i] = res[i - 1] * nums[i - 1];
       }
       int right = 1;
       for (int i = n - 1; i >= 0; i--) {
          res[i] *= right;
          right *= nums[i];
      }
       return res;
    }
}

二、树相关

1.给定一颗二叉搜索树，返回该二叉搜索树第K大的节点

//思路：二叉搜索树按照中序遍历的顺序打印出来正好就是排序好的顺序。
//     所以，按照中序遍历顺序找到第k个结点就是结果。
public class Solution {
   int index = 0; //计数器
    TreeNode KthNode(TreeNode root, int k)
    {
        if(root != null){ //中序遍历寻找第k个
            TreeNode node = KthNode(root.left,k);
            if(node != null)
                return node;
            index ++;
            if(index == k)
                return root;
            node = KthNode(root.right,k);
            if(node != null)
                return node;
        }
        return null;
    }
}

 2.二叉树最小深度

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
//为什么采用分治的思想而不是求数最大深度思想，因为可能为单链表（链表是特殊树）没法处理
class Solution {
     public int minDepth(TreeNode root) {
        if(root == null) return 0;
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        return (left == 0 || right == 0) ? left + right + 1//为什么可以写成left + right + 1
            : Math.min(left,right) + 1;         //因为left 跟right 必有一个为0，所以..
       
    }
}

3.二叉树最大深度

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
   public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        } else{
            return 1+ Math.max(maxDepth(root.left), maxDepth(root.right));
        }
    }
}

三、动态规划相关

1.两个字符串的最长公共子序列长度

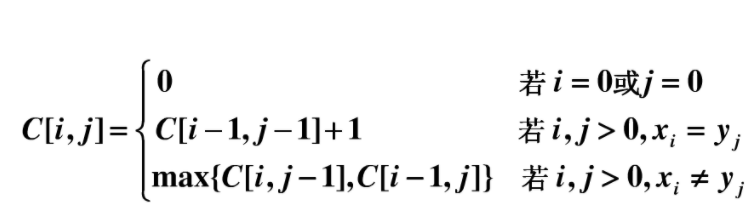
class Solution {
//dp[i][j]表示 0-(i-1) 0-(j-1)之间最长子序列
    public int longestCommonSubsequence(String s1, String s2) {
        int[][] dp = new int[s1.length() + 1][s2.length() + 1];
        for (int i = 0; i < s1.length(); ++i)
            for (int j = 0; j < s2.length(); ++j)
                if (s1.charAt(i) == s2.charAt(j)) dp[i + 1][j + 1] = 1 + dp[i][j];
                else dp[i + 1][j + 1] =  Math.max(dp[i][j + 1], dp[i + 1][j]);
        return dp[s1.length()][s2.length()];
    }
}

2.求连续子数组的最大和

class Solution {
   public static int maxSubArray(int[] A) {
    int maxSoFar=A[0], maxEndingHere=A[0];
    for(int i=1;i<A.length;++i){
        maxEndingHere = Math.max(A[i], maxEndingHere+A[i]);
        maxSoFar = Math.max(maxEndingHere, maxSoFar);
    }
    return maxSoFar;
  }
}

四、排序

1.快排

public static void quickSort(int[] list, int left, int right) {
        if (left < right) {
            // 分割数组，找到分割点
            int point = partition(list, left, right);

            // 递归调用，对左子数组进行快速排序
            quickSort(list, left, point - 1);
            // 递归调用，对右子数组进行快速排序
            quickSort(list, point + 1, right);
        }
    }

    /**
     * 分割数组，找到分割点
     */
    public static int partition(int[] list, int left, int right) {
        // 用数组的第一个元素作为基准数
        int first = list[left];
        while (left < right) {
            while (left < right && list[right] >= first) {
                right--;
            }
            // 交换
            swap(list, left, right);

            while (left < right && list[left] <= first) {
                left++;
            }
            // 交换
            swap(list, left, right);
        }
        // 返回分割点所在的位置
        return left;
    }

    /**
     * 交换数组中两个位置的元素
     */
    public static void swap(int[] list, int left, int right) {
        int temp;
        if (list != null && list.length > 0) {
            temp = list[left];
            list[left] = list[right];
            list[right] = temp;
        }
    }

 2.二路归并排序

public class MergeSort {
    /**
     * 归并排序（Merge Sort）与快速排序思想类似：将待排序数据分成两部分，继续将两个子部分进行递归的归并排序；然后将已经有序的两个子部分进行合并，最终完成排序。
     * 其时间复杂度与快速排序均为O(nlogn)，但是归并排序除了递归调用间接使用了辅助空间栈，还需要额外的O(n)空间进行临时存储。从此角度归并排序略逊于快速排序，但是归并排序是一种稳定的排序算法，快速排序则不然。
     * 所谓稳定排序，表示对于具有相同值的多个元素，其间的先后顺序保持不变。对于基本数据类型而言，一个排序算法是否稳定，影响很小，但是对于结构体数组，稳定排序就十分重要。例如对于student结构体按照关键字score进行非降序排序：
     */
    public static void main(String[] args) {
        int[] list = {50, 10, 90, 30, 70};
        System.out.println("************归并排序************");
        System.out.println("排序前：");
        display(list);
        System.out.println("排序后：");
        mergeSort(list, new int[list.length], 0, list.length - 1);
        display(list);
    }

    /**
     * 归并排序算法
     * @param list     待排序的列表
     * @param tempList 临时列表
     * @param head     列表开始位置
     * @param rear     列表结束位置
     */
    public static void mergeSort(int[] list, int[] tempList, int head, int rear) {
        if (head < rear) {
            // 取分割位置
            int middle = (head + rear) / 2;
            // 递归划分列表的左序列
            mergeSort(list, tempList, head, middle);
            // 递归划分列表的右序列
            mergeSort(list, tempList, middle + 1, rear);
            // 列表的合并操作
            merge(list, tempList, head, middle + 1, rear);
        }
    }

    /**
     * 合并操作(列表的两两合并)
     * @param list
     * @param tempList
     * @param head
     * @param middle
     * @param rear
     */
    public static void merge(int[] list, int[] tempList, int head, int middle, int rear) {
        // 左指针尾
        int headEnd = middle - 1;
        // 右指针头
        int rearStart = middle;
        // 临时列表的下标
        int tempIndex = head;
        // 列表合并后的长度
        int tempLength = rear - head + 1;

        // 先循环两个区间段都没有结束的情况
        while ((headEnd >= head) && (rearStart <= rear)) {
            // 如果发现右序列大，则将此数放入临时列表
            if (list[head] < list[rearStart]) {
                tempList[tempIndex++] = list[head++];
            } else {
                tempList[tempIndex++] = list[rearStart++];
            }
        }

        // 判断左序列是否结束
        while (head <= headEnd) {
            tempList[tempIndex++] = list[head++];
        }

        // 判断右序列是否结束
        while (rearStart <= rear) {
            tempList[tempIndex++] = list[rearStart++];
        }

        // 交换数据
        for (int i = 0; i < tempLength; i++) {
            list[rear] = tempList[rear];
            rear--;
        }
    }

    /**
     * 遍历打印
     */
    public static void display(int[] list) {
        if (list != null && list.length > 0) {
            for (int num :list) {
                System.out.print(num + " ");
            }
            System.out.println("");
        }
    }
}

五、LRU LFU

1.lru采用双链表+hashmap实现

class LRUCache {
    int size;
    Node head,tail;
    HashMap<Integer,Node> hm;
    public LRUCache(int capacity) { 
         size=capacity;
         head=tail=null;
         hm=new HashMap<>();
    }
    
    public int get(int key) {
        
         if(!hm.containsKey(key))
         {
             return -1;
         }
         else
         {
             Node ref=hm.get(key);
             if(ref==head) return ref.val;
             if(ref!=head && ref!=tail)
             {
                 ref.Llink.Rlink=ref.Rlink;
                 ref.Rlink.Llink=ref.Llink;
                 
             }
             else if(ref!=head && ref==tail)
             {
                 tail=tail.Llink;
                 tail.Rlink=null;
                 
             }
             ref.Llink=null;
             ref.Rlink=head;
             head.Llink=ref;
             head=ref;
             return ref.val;
         }
        
        
      
    }
    
    public void put(int key, int value) {
      
         if(hm.containsKey(key))
         {
             hm.get(key).val=value;
             this.get(key);
         }
         else
         {
             Node temp=new Node(value,key);
            
             if(hm.size()<size)
             {   hm.put(key,temp);
                 if(head==null)
                 {
                     head=temp;
                     tail=temp;
                 }
                 else
                 {
                     temp.Rlink=head;
                     head.Llink=temp;
                     head=temp;
                 }
             }
             else
             {
                 if(tail==head)
                 {
                     hm.remove(tail.key);
                     hm.put(key,temp);
                     head=tail=temp;
                 }
                 else
                 {
                     hm.remove(tail.key);
                     hm.put(key,temp);
                     Node help=tail;
                     tail=tail.Llink;
                     tail.Rlink=null;
                     help.Llink=null;
                     temp.Rlink=head;
                     head.Llink=temp;
                     head=temp;
                 }
                  
                    
             }
             
         }
        
        
    }    
}

class Node{
    int val;
    int key;
    Node Rlink;
    Node Llink;
    Node(int val,int key)
    {   this.key=key;
        this.val=val;
        Rlink=null;
        Llink=null;
    }
   
}

2.lfu