函数连续:函数 $f(x)$ 在某一个点 $x_{0}$ 处连续必须同时满足 3 个条件:
1)函数在 $x_{0}$ 处有定义
2)$lim_{x ightarrow x_{0}}f(x)$ 存在
3)$lim_{x ightarrow x_{0}}f(x) = f(x_{0})$
函数间断:函数 $f(x)$ 在某一个点 $x_{0}$ 的去心邻域有定义,但在点 $x_{0}$ 不连续,即上面三个条件不全满足,则函数在该点间断,
该点为间断点。间断点可以有定义也可无定义,间断只是考虑极限,而极限只与该点左右极限有关,和点的取值无关。
1)第一类间断点
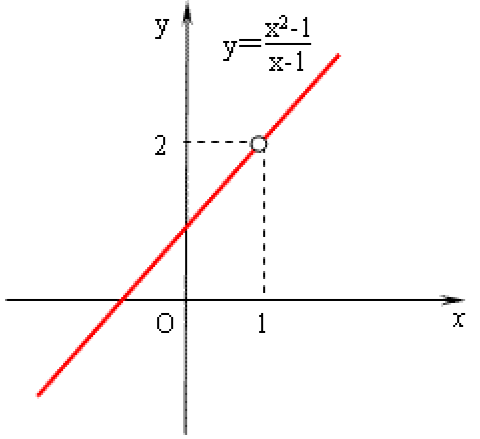
a. 可去间断点:函数 $f(x)$ 在 $x_{0}$ 处左右极限都存在且相等,即该点处极限存在。若 $f(x)$ 在 $x_{0}$ 处有定义,则$lim_{x ightarrow x_{0}}f(x) eq f(x_{0})$。

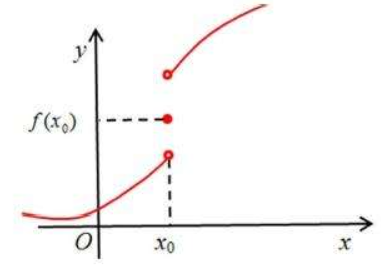
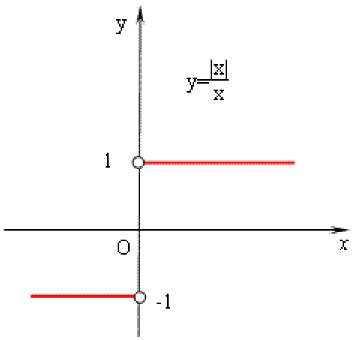
b. 跳跃间断点:$f(x)$ 在 $x_{0}$ 处左右极限都存在但不相等。
2)第二类间断点
a. 无穷间断点:左右极限至少有一个不存在(不存在就是为 $infty$ )。

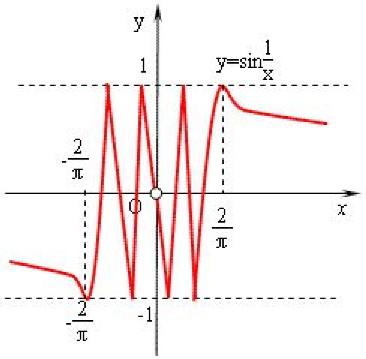
b. 振荡间断点:间断点处的极限振荡不存在,此处是振荡不存在,并不是极限为无穷。下图函数,当 $x ightarrow 0$,函数值在 -1和1之间交替取值。