人工神经网络是一个数学模型,旨在模拟人脑的神经系统对复杂信息的处理机制,其网络结构是对人脑神经元网络的抽象,两者有很多相似之处。
当然 ANN 还远没有达到模拟人脑的地步,但其效果也让人眼前一亮。
1. 人工神经元结构
人工神经元是一个多输入单输出的信息处理单元,是对生物神经元的建模。建模方式可以有很多种,不同的建模方式就意味着不同的人工神经元结构。
比较著名的人工神经元模型是 MP 神经元,直到今天,我们仍然在使用这个神经元模型。MP 神经元是模仿生物的神经元设计的:
1)输入向量 $x$ 模拟生物神经元中其他神经细胞给该细胞的刺激,值越大刺激越大;
2)$w$ 向量模拟该细胞不同来源的刺激的敏感度;
3)用阈值 $ heta$ 来描述激活该神经元的难易程度,越大越难激活;
4)用 $w_{1}x_{1} + w_{2}x_{2} + ... + w_{n}x_{n} - heta$ 来计算神经元的兴奋程度;
5)$y = f(x)$ 为激活函数,用来计算神经元的输出,因为生物神经元的输出是有上下限的,所以激活函数也是能够“饱和”的有界函数;
6)在 MP 神经元中,激活函数为阶梯函数。兴奋函数大于阈值输出 $1$,小于阈值输出 $0$;
下图是 MP 神经元模型的示意图:
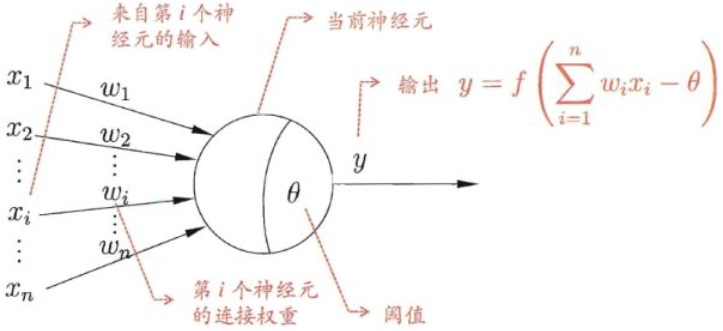
将激活函数代入,将项 $- heta$ 设为 $b$,则可以得到 MP 神经元的数学模型:
$$y = sgn left ( sum_{i=1}^{n}(w_{i}x_{i} + b) ight ) = sgn left ( w^{T}x + b ight )$$
惊讶得发现它就是一个线性分类模型,和感知机的数学模型是完全一样的,所以一个 MP 神经元的作用就是:对输入进行二分类。
这是符合生物神经元的特点的,因为一个生物神经元对输入信号所产生的作用就是:兴奋或这抑制。
所以通俗来讲:一条直线把平面一分为二,一个平面把三维空间一分为二,一个 $n-1$ 维超平面把 $n$ 维空间一分为二,两边分属不同的两类,
这种分类器就叫做神经元,一个神经元只能分两类,输出是一个能体现类别的标量。
一个神经元的作用就是这么简单,所做的也只能是线性分类,但是当多个神经元互联的时候就会产生神奇的效果,下面再叙述。
MP 神经元的输出是样本点所属的类别,它把直线一侧变为 $0$,另一侧变为 $1$,这东西不可微,不利于数学分析,经常用其它类似于 $sgn$ 的可微
函数来做激活函数,如:

用上面的激活函数,比使用符号函数能体现样本的更多信息。
2. 多层感知器
由于 MP 神经元的输入来自于其他神经元,我们显然不能指望单独一个神经元就有什么功能,而多个神经元可以组成不同的结构。
下面介绍一个二层感知器,来直观得感受下神经网络到底是如何工作的?其网络结构图如下:
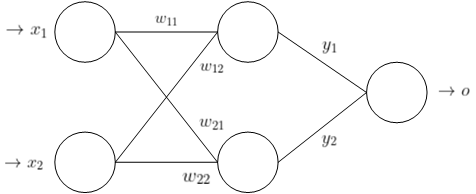
用这个网络对输入 $(0,0),(0,1),(1,0),(1,1)$ 四个点进行分类,其中红点是一类,蓝点是一类,使用的激活函数是 $sgn$。
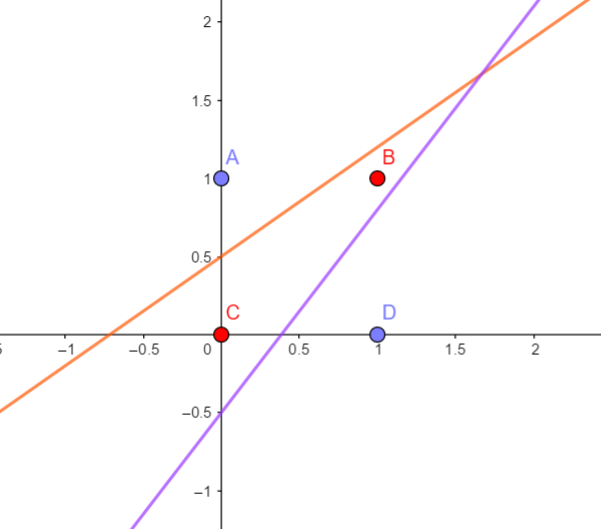
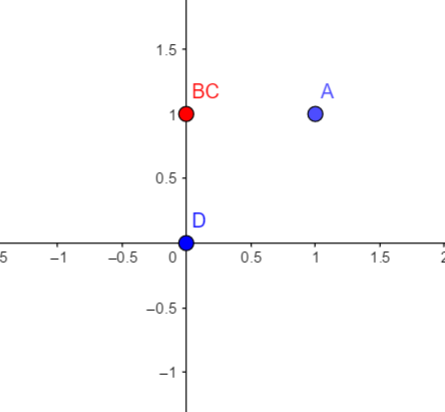
因为一个神经元的作用就是切一刀,即做一次线性分割,很显然对于上面的四个点没有办法只切一刀就完成分类,于是考虑用两个神经元,
即现在隐藏层有两个神经元,即再切一刀,现在我们分析一下隐藏层两个神经元的输出情况:
$$x_{1} ;;; x_{2} ;;; y_{1} ;;; y_{2} \
0 ;;;;; 1 ;;;; 1 ;;;;; 1 \
0 ;;;;; 0 ;;;; 0 ;;;;; 1 \
1 ;;;;; 1 ;;;; 0 ;;;;; 1 \
1 ;;;;; 0 ;;;; 0 ;;;;; 0$$
我们将隐藏层的输出 $(y_{1},y_{2})$ 绘制在坐标系上,如上右图。神奇的事情发生了,原本无法一刀切的四个点,经过隐藏层
的后,变成了线性可分的,此时通过一条直线可以完成分类,所以输出层的神经元一个就够了。
神经网络是由一层一层构建的,那么每层究竟在做什么呢?
由上面的例子可以理解到,每一层神经元就是用线性变换跟随着非线性变化,将输入空间投向另一个空间,变换手段有:
1)升维/降维
2)放大/缩小
3)旋转
4)平移
5)弯曲
其中 $1,2,3$ 操作由 $w^{T}x$ 完成,$4$ 操作由 $+b$ 完成,$5$ 操作由激活函数 $f$ 完成。
我们知道空间是由基决定的,首先我们先定义一个参考系 $S_{1}$,整个神经网络以它为坐标系。
将一个变换作用在一个向量上面,该怎么理解为空间的改变呢?举一个例子;在参考系 $S_{1}$ 下面的一个向量 $(a,b)$,将它做如下变换:
$$ai^{'} + bj^{'}$$
其中 $i^{'},j^{'}$ 线性无关,那么这个输出相当于以向量 $i^{'},j^{'}$ 为基(参考系还是 $S_{1}$)进行合成,因为基 $i^{'},j^{'}$ 本身就可
以表示一个空间,变换本质在这个空间里进行与原空间 $S_{1}$ 相同效果的向量合成,只不过新的空间是以参考系 $S_{1}$ 来进行坐标表示的。
关键就在于变化前后的参考系没有改变,那么只要有足够的合适的神经元,空间的扭曲形变终究会使样本点线性可分。
注:这个地方理解得不对,参考系也变化到对应维度的空间去了。
3. 神经网络模型训练算法
1)单层感知器梯度下降法
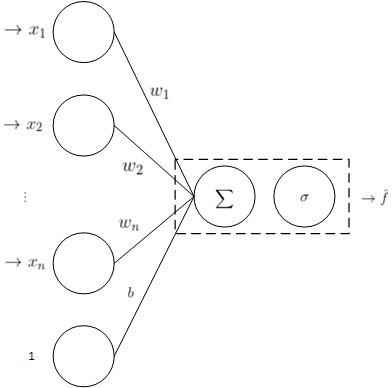
激活函数为 $sigma(u)$,故该网络的数学模型:
$$hat{f} = sigma(w^{T}x + b)$$
对于一个输入向量,期望的网络输出为 $f$(训练集中已知的量),模型的实际输出为 $hat{f}$,损失函数定义为:
$$L(w,b) = frac{1}{2} left ( f - hat{f} ight )^{2} = frac{1}{2} left [ f - sigma(w^{T}x + b) ight ]^{2}$$
这个误差只是针对一个样本点的,除以 $2$ 的目的仅是为了求梯度时更好看,训练的时候是一个一个样本代入求损失函数的最小值,是随机梯度下降法。
需要确定的参数是 $w_{i},i = 1,2,...,n$ 和 $b$,根据链式法则求偏导得:
$$frac{partial L}{partial w_{i}} = frac{partial L}{partial hat{f}} cdot frac{partial sigma}{partial u} cdot frac{partial u}{partial w_{i}} = - left ( f - hat{f}
ight ) cdot x_{i} cdot frac{partial sigma}{partial u}
; Rightarrow ; frac{partial L}{partial w} = left ( f - hat{f}
ight ) cdot X cdot frac{partial sigma}{partial u} \
frac{partial L}{partial b} = frac{partial L}{partial hat{f}} cdot frac{partial sigma}{partial u} cdot frac{partial u}{partial b} = - left ( f - hat{f}
ight ) cdot frac{partial sigma}{partial u}$$
所以参数更新方法为:
$$w = w + eta left ( f - hat{f}
ight ) cdot X cdot frac{partial sigma}{partial u} \
b = b + eta left ( f - hat{f}
ight ) cdot frac{partial sigma}{partial u}$$
2)多层感知器的反向传播算法
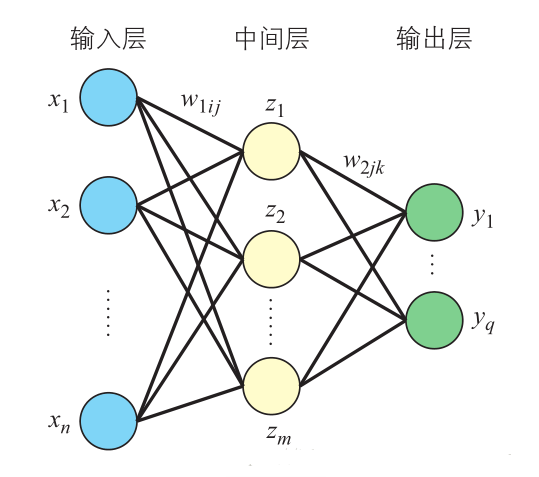
图中 $i$ 表示输入层单元,$j$ 表示中间层单元,$k$ 表示输出层单元。多层感知器的误差函数 $L(w,b)$ 等于个输出单元的误差总和,即
$$L(w,b) = frac{1}{2}sum_{k=1}^{q}(r_{k} - y_{k})^{2}$$
$r_{k}$ 表示期望的输出,是已知量(训练集提供),$y_{k}$ 为模型的实际输出,设激活函数为 $sigma(u)$。
先来看一下各层的函数关系:
$$y_{k} = sigma_{2k} left ( sum_{j=1}^{m}w_{2jk}z_{j} + b_{2k}
ight ) \
z_{j} = sigma_{1j} left ( sum_{i=1}^{n}w_{1ij}x_{i} + b_{1j}
ight )$$
需要确定的参数就是 $w_{1ij},w_{2jk},b_{1j},b_{2k}$,对每一层的各个参数求偏导有:
$$frac{partial L}{partial w_{2jk}} = frac{partial L}{partial y_{k}} cdot frac{partial sigma_{2k}}{partial u_{2k}} cdot frac{partial u_{2k}}{partial w_{2jk}} = -(r_{k} - y_{k}) cdot z_{j} cdot frac{partial sigma_{2k}}{partial u_{2k}}$$
$$frac{partial L}{partial w_{1ij}} = sum_{k=1}^{q}frac{partial L}{partial y_{k}} cdot frac{partial sigma_{2k}}{partial u_{2k}} cdot frac{partial u_{2k}}{partial z_{j}} cdot frac{partial sigma_{1j}}{partial u_{1j}} cdot frac{partial u_{1j}}{partial w_{1ij}} = -sum_{k=1}^{q}(r_{k} - y_{k}) cdot frac{partial sigma_{2k}}{partial u_{2k}} cdot w_{2jk} cdot frac{partial sigma_{1j}}{partial u_{1j}} cdot x_{i}$$
假设激活函数为 $sigmod$,上面的过程可总结为下面两张图,图中的 $E$ 就是误差函数 $L$。
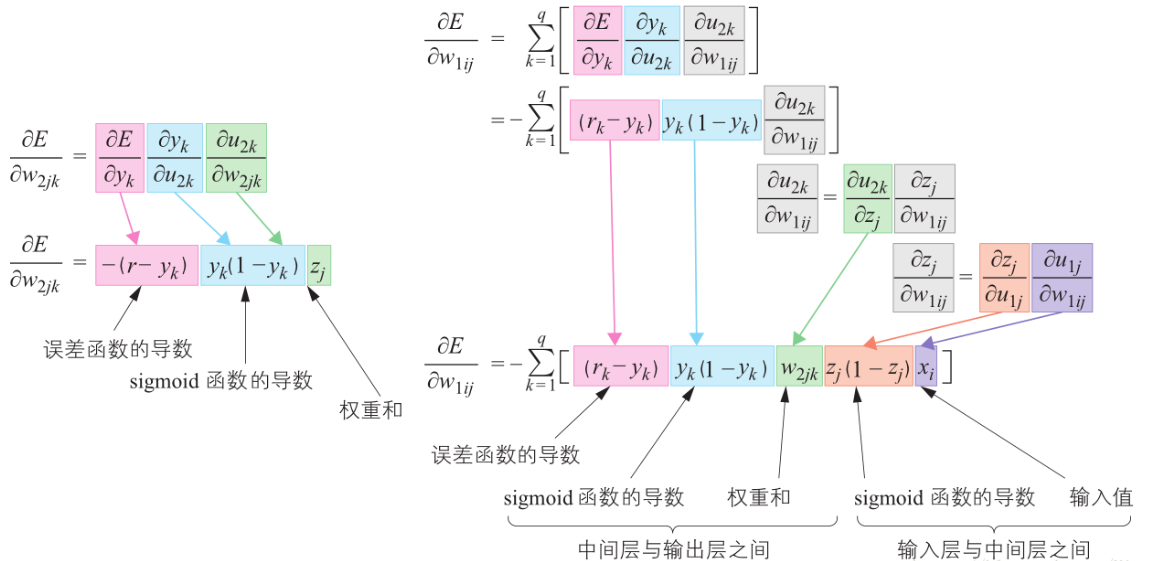
纵观整个过程,对于 ANN,当我们需要使用它时,是从最前面给出输入,然后一步步往后计算得出这个庞大复杂函数的输出的;
而当我们需要训练它时,则是从最后面的参数开始,一步步向前求导,调整各个参数的。并且计算前面的参数时一般都会用到之前计算过的中间结果。
这样,ANN 调整参数的过程就可以看作是一个误差反向传播(BP)的过程。