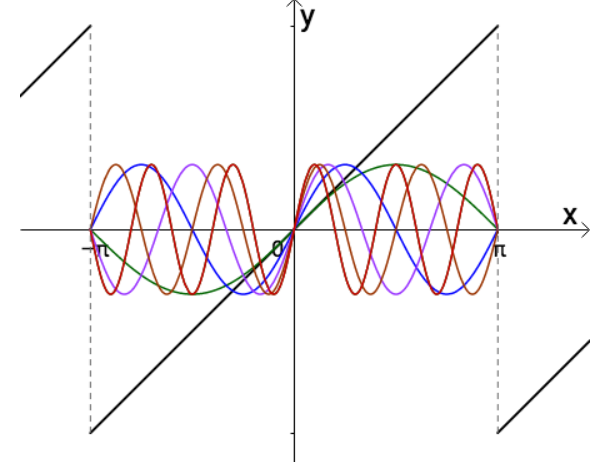
拉格朗日等数学家发现某些周期函数可以由三角函数的和来表示,比如下图中,黑色的斜线是周期为 $2pi$ 的函数,而红色的曲线是三角函数
之和,可以看出两者确实近似:

另一位数学家傅里叶猜测任意周期函数都可以写成三角函数之和。
首先先证明一个结论:任意一个函数都可拆分成一个偶函数和一个奇函数的和。
证明
易知
$$f(x) = frac{f(x) - f(-x)}{2} + frac{f(x) + f(-x)}{2} = g(x) + h(x)$$
因为
$$g(-x) = frac{f(-x) - f(x)}{2} = -g(x) \
h(-x) = frac{f(-x) + f(x)}{2} = h(x)$$
所以 $g(x)$ 是奇函数,$h(x)$ 是偶函数,即 $f(x)$ 可以展开为奇函数和偶函数的和。
证毕
傅里叶就试图将周期为 $T$ 的函数 $f(x)$ 展开为 $sin x$ 和 $cos x$ 函数和的形式。
那怎么保证组合出来的函数周期依然为 $T$ 呢?
我们知道函数 $f = sin omega t$ 的周期为 $T^{'} = frac{2pi}{omega}$,要使得原函数能够被三角函数表示,那么三角函数的粒度必然要小于原函数,
即三角函数的最小周期 $T^{'}$ 必须小于原函数 $f(x)$ 的最小周期 $T$,即
$$frac{2pi}{omega} leq T \
Rightarrow frac{2pi n}{omega} = T, ; n > 0$$
这里的 $n$ 必须是一个整数,对于周期函数,它的分量的角频率也必定是原函数角频率的整数倍,这一点不做证明。
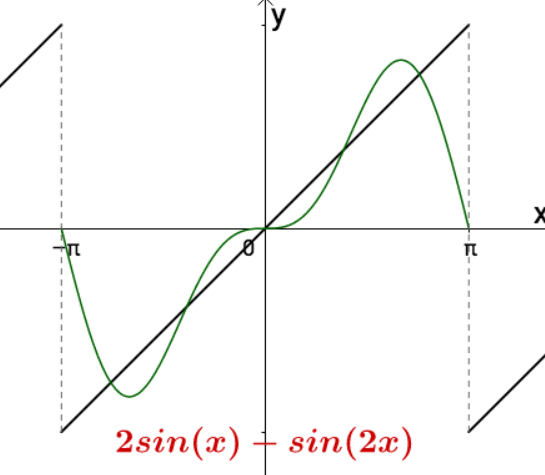
现在我们有了各种三角函数,如 $sin x,sin 2x,sin 3x,sin 4x$,对于最初举的周期为 $2pi$ 的函数,可以用这些三角函数慢慢逼近。
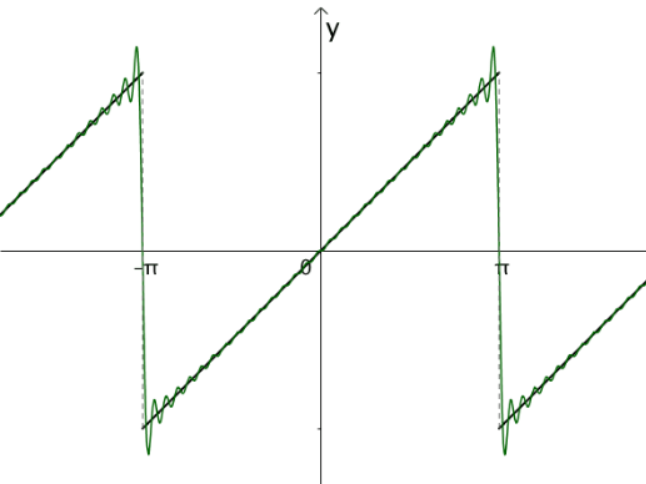
综上,构造出来的三角函数展开式形式为
$$f(x) = sum_{n = 1}^{infty}left ( a_{n}cos frac{2pi n}{T}x + b_{n}sin frac{2pi n}{T}x ight ) + C$$
其中 $frac{2pi}{T}$ 是原始信号的角频率,因为 $n > 1$,可见分量的角频率必然不小于原始信号的频率,是原始信号频率的整数倍。所以这里的 $n$
不要认为是索引序号,而是分量的角频率与原始信号角频率的倍数关系,如果没有某个倍数对应的分量,那么这一项就是 $0$。
那怎么确定参数 $C,a_{n},b_{n}$ 呢?先来了解一下三角函数的正交性。
三角函数系列 $1,cos x, sin x, cos 2x, sin 2x,..., cos nx, sin nx,...$,在区间 $left [ -pi, +pi ight ]$ 上是正交函数系,即
$$int_{-pi}^{pi}cos nxdx = 0, (n = 1,2,3,...) ;;; int_{-pi}^{pi}sin nxdx = 0, (n = 1,2,3,...) \
int_{-pi}^{pi}cos mx sin nx dx = 0, (m,n = 1,2,3,...) \
int_{-pi}^{pi}cos mx cos nx dx = 0, (m,n = 1,2,3,..., m
eq n) ;;; int_{-pi}^{pi}sin mx sin nx dx = 0, (m,n = 1,2,3,..., m
eq n) $$
比如,我们要求 $cos frac{2pi n}{T}x$ 这一项的系数,两边都乘上它,然后两边在 $0-T$ 积分,注意这里的 $T$ 是原始信号的周期,但因为 $n > 1$,所以分解的
分量信号的周期都会比 $T$ 小而且是整数倍,那么依然可以用正交性,就会发现只留下自身那一项,基于此可求得

求 $C$ 的话,两边直接在 $0-T$ 上积分即可,可求得
$$C = frac{a_{0}}{2}$$
在求系数的公式中,$T,f(x)$ 都是已知的,所以只要给定一个周期信号,我们就能通过傅里叶级数分解为一个一个的正弦或余弦分量,求系数很容易,
代公式算即可,难的是为什么一个周期信号一定可以分解为三角函数求和的形式,傅里叶级数展开的形式是怎么来的?这里就不做证明了。
根据欧拉公式,我们来推导一下傅里叶级数的指数形式:
$$f(x) = frac{a_{0}}{2} + sum_{n = 1}^{infty}left ( a_{n}cos nomega x + b_{n}sin nomega x
ight ) \
= frac{a_{0}}{2} + sum_{n = 1}^{infty}left [ a_{n}frac{e^{inomega x} + e^{-inomega x}}{2} + b_{n}frac{e^{inomega x} - e^{-inomega x}}{2i}
ight ] \
= frac{a_{0}}{2} + sum_{n = 1}^{infty}left [ frac{a_{n} - ib_{n}}{2}e^{inomega x} + frac{a_{n} + ib_{n}}{2}e^{-inomega x}
ight ]$$
其中,$omega$ 是原始信号的角频率,$nomega$ 是分量的角频率,也可写成 $omega_{n}$,因为
$$frac{a_{n} - ib_{n}}{2} = frac{1}{T}int_{0}^{T}f(x)cos nomega xdx - ifrac{1}{T}int_{0}^{T}f(x)sin nomega xdx \
= frac{1}{T}int_{0}^{T}f(x)left (cos nomega x - isin nomega x
ight )dx \
= frac{1}{T}int_{0}^{T}f(x)e^{-inomega x}dx, ; n = 1,2,3,cdots $$
$$frac{a_{n} + ib_{n}}{2} = frac{1}{T}int_{0}^{T}f(x)cos nomega xdx + ifrac{1}{T}int_{0}^{T}f(x)sin nomega xdx \
= frac{1}{T}int_{0}^{T}f(x)left (cos nomega x + isin nomega x
ight )dx \
= frac{1}{T}int_{0}^{T}f(x)e^{inomega x}dx, ; n = 1,2,3,cdots$$
$$frac{a_{0}}{2} = frac{1}{T}int_{0}^{T}f(x)dx$$
惊讶得发现
$$frac{a_{n} - ib_{n}}{2} ; xrightarrow[]{let ; n = -n} ; frac{a_{n} + ib_{n}}{2} \
frac{a_{n} - ib_{n}}{2} ; xrightarrow[]{let ; n = 0} ; frac{a_{0}}{2}$$
若令
$$c_{n} = frac{1}{T}int_{0}^{T}f(x)e^{-inomega x}dx \
= frac{1}{T}int_{0}^{T}f(x)e^{-iomega_{n} x}dx, ; n =0, pm 1, pm 2, pm 3, cdots$$
其中 $omega_{n}$ 是分量的角频率,则傅里叶级数展开可以写出如下形式:
$$f(x) = sum_{n = -infty}^{+ infty} c_{n}e^{-inomega x} = sum_{n = -infty}^{+ infty} c_{n}e^{-iomega_{n} x}, ;; n in Z$$
指数形式的傅里叶级数展开比三角形式的简洁,前者只需要求一个参数 $c_{n}$,而后者需要求三个参数 $a_{n},b_{n},a_{0}$。
由欧拉公式我们知道,$e^{j heta}$ 表示复平面上的一个旋转了 $ heta$ 弧度的向量,那么指数形式的傅里叶形式就可以理解为:无数旋转的叠加。
或者说是:圆周运动的组合。
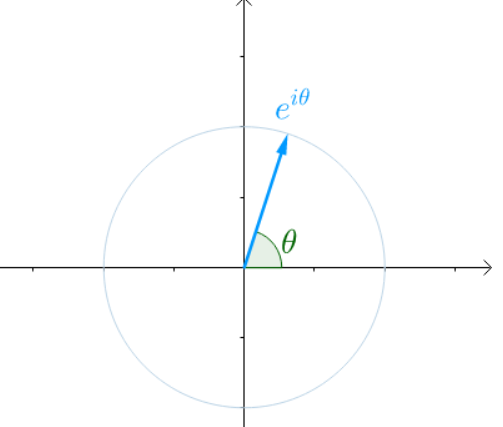

因为欧拉公式的存在,正弦函数或者余弦函数以及它们的组合就可以看成虚数 $e^{j heta}$ 的实部或者虚部,也就提供了另一个角度来观察函数 $f(x)$
的展开分量,原来的级数展开是时域上的各个信号相加,到复平面之后,它的分量就变成了一个个向量 $e^{jomega t}$,在以各自的角频率旋转。比如上面
右图中所示就是函数 $g(x)$ 分解为两个正弦分类后在复平面上的情况:
$$g(x) = sin x + sin 2x \
Rightarrow e^{ix} = cos x + i sin x ;; e^{i2x} = cos 2x + i sin 2x \
Rightarrow e^{ix} + e^{i2x} = (cos x + cos 2x) + i(sin x + sin 2x)$$
那么 $g(x)$ 的时域图像就是向量 $e^{ix}$ 和 $e^{i2x}$ 在复平面上合成后的虚轴变化情况。
频谱一般分为幅度谱和相位谱两种,那怎么画幅度谱呢?幅度谱是哪两个量之间的关系呢?幅度谱分为两种
1)单边幅度谱
只考虑频率为正数部分得到的频谱,由三角形式的傅里叶级数得到,根据三角函数的归一公式是可以只保留正弦函数或余弦函数的,即
$$f(x) = frac{a_{0}}{2} + sum_{n = 1}^{infty}left ( a_{n}cos nomega x + b_{n}sin nomega x
ight ) \
= c_{0} + sum_{n = 1}^{infty}c_{n}cosleft ( nomega x + varphi_{n}
ight)$$
其中
$$varphi_{n} = -arctan frac{b_{n}}{a_{n}} \
c_{n} = sqrt{a_{n}^{2} + b_{n}^{2}}, n = 1,2,3,cdots \
c_{0} = frac{a_{0}}{2}$$
单边幅度谱就是 $c_{n},n = 1,2,3,...$ 关于 $nomega$ 的离散的图像。
2)双边幅度谱
由指数形式的傅里叶级数推导过程可知:
$$c_{n} = frac{1}{T}int_{0}^{T}f(x)e^{-inomega x}dx, ; n =0, pm 1, pm 2, pm 3, cdots$$
因为 $c_{n}$ 是一个复数,可以可以写成模和辐角的形式,即
$$c_{n} = left | c_{n} ight |e^{ivarphi_{n}}, ; n =0, pm 1, pm 2, pm 3, cdots$$
又因为
$$c_{n} = frac{a_{n} - ib_{n}}{2}, ; n =0, pm 1, pm 2, pm 3, cdots$$
所以
$$left |c_{n}
ight | = frac{sqrt{a_{n}^{2} + b_{n}^{2}}}{2} \
varphi_{n} = -arctan frac{b_{n}}{a_{n}}$$
双边幅度谱就是 $c_{n},n = 0, pm1,pm2,pm3,...$ 关于 $nomega$ 的离散的图像。
可以看出,除了 $n = 0$,双边幅度谱的高度是单边幅度谱的一半,在 $n = 0$ 两者高度的绝对值相等。