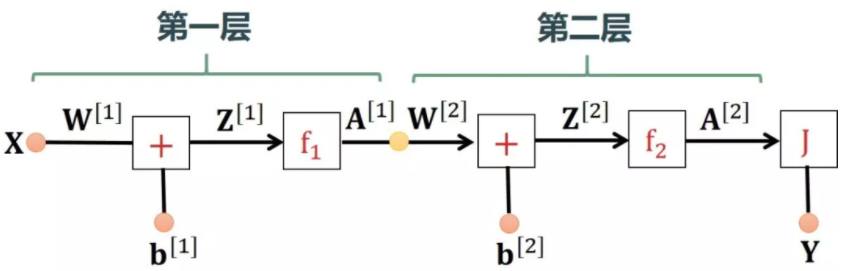
张量求导规则 $frac{partial y}{partial x}$
1. 规则 $1$:形状规则
a. 只要 $y$ 或 $x$ 中有一个是标量,那么导数 $frac{partial y}{partial x}$ 的形状和非标量的形状一致。
b. 如果 $y$ 和 $x$ 都是非标量,那么把 $y$ 拆成一个个标量元素,先求每个标量元素对 $x$ 的导数,结果张量的形状规则按 $a$ 中要求,
然后所有标量元素的求导结果按 $y$ 的形状排列。
举个例子:$y$ 的形状为 $(3,4)$,$x$ 的形状为 $(4,8,1)$,那么求导结果的张量形状为?按照形状规则,$y$ 中每个标量元素对 $x$ 的求导结果形状与 $x$ 相同,
即$(4,8,1)$,所有标量对 $x$ 的求导结果再按 $y$ 的形状排列,所以整个求导结果张量的形状为 $(3,4,4,8,1)$。
这个规则是最基本也是最重要的形状规则,无论是向量对向量求导、向量对矩阵求导还是矩阵对矩阵求导,最终都可以分解为标量对矩阵求导的组合,
就可以判断出求导结果的形状。
2. 规则 $2$:当 $y, x$ 都是列向量且 $y = Wx$,有 $frac{partial y}{partial x} = W$;当 $y, x$ 都是行向量且 $y = xW$,有 $frac{partial y}{partial x} = W^{T}$。
在 Pytorch 只有向量乘向量或矩阵乘矩阵,不存在矩阵和向量相乘,如果出现矩阵和向量相乘,Pytorch 内部会对向量增加一个前置尺寸后者后置尺寸,
使向量变成一个矩阵以满足形状要求,本质还是矩阵乘矩阵,运算完成后,删除输出结果的尺寸,结果就还是一个向量。
形状为 $(m,)$ 的向量 $y$ 对形状为 $(n,)$ 的向量 $x$ 求导,根据形状规则 $1$,向量 $y$ 的每个标量元素对向量 $x$ 的求导结果的形状为 $(n,)$,
即与 $x$ 相同,最后在前面加上 $y$ 的形状,所以结果张量的形状为 $(m,n)$,

3. 现在关注向量对矩阵求导,存在两种关系:
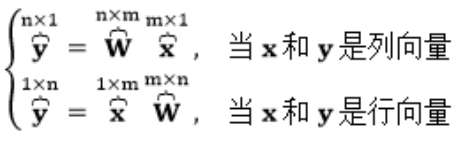
1)列向量 $y$ 对矩阵 $W$ 求导,其中 $y_{n imes 1} = W_{n imes m}x_{m imes 1}$
根据向量 $y(n imes 1)$ 和矩阵 $W(n imes m)$ 的大小,$frac{partial y}{partial W}$ 是个三维张量,形状为 $n imes (n imes m)$。形式如下:
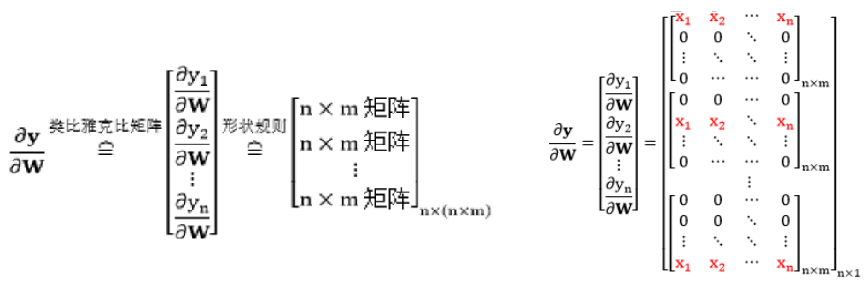
按照形状规则 $1$,$frac{partial y_{i}}{partial W}$ 的形状和矩阵 $W$ 的形状是一样的。
2)行向量 $y$ 对矩阵 $W$ 求导,其中 $y_{1 imes n} = x_{1 imes m}W_{m imes n}$
根据向量 $y(1 imes n)$ 和矩阵 $W(m imes n)$ 的大小,$frac{partial y}{partial W}$ 是个三维张量,形状为 $n imes (m imes n)$。形式如下:

按照规则 $1$,$frac{partial y_{i}}{partial W}$ 的形状和矩阵 $W$ 的形状是一样的。
对于误差函数 $J$,它是 $y$ 的标量函数。下面我们来求一求 $frac{partial J}{partial W}$。
1)列向量 $y$ 对矩阵 $W$ 求导,其中 $y_{n imes 1} = W_{n imes m}x_{m imes 1}$

2)行向量 $y$ 对矩阵 $W$ 求导,其中 $y_{1 imes n} = x_{1 imes m}W_{m imes n}$
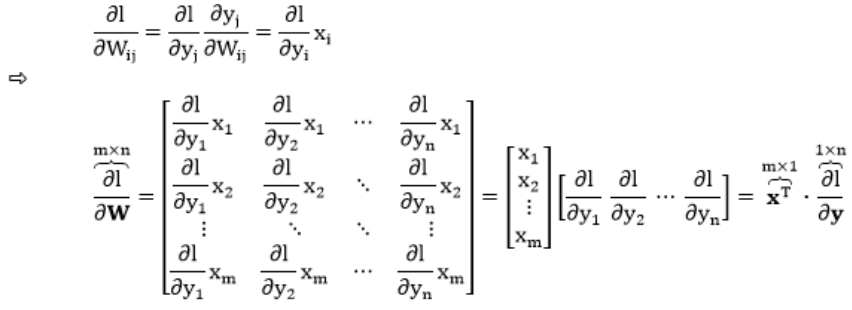
规则 $3$ 总结如下:
a. 当 $y, x$ 都是列向量且 $y = Wx$,$l$ 是 $y$ 的标量函数,有 $frac{partial l}{partial W} = frac{partial l}{partial y} cdot x^{T}$。
b. 当 $y, x$ 都是行向量且 $y = xW$,$l$ 是 $y$ 的标量函数,有 $frac{partial l}{partial W} = x^{T} cdot frac{partial l}{partial y}$。
4. 假设 $X$ 是 $d imes m$ 的矩阵,$W$ 是 $n imes d$ 的矩阵,而 $Y = WX$ 是 $n imes m$ 的矩阵,以 $d = 3, m = 2, n = 2$ 为例。
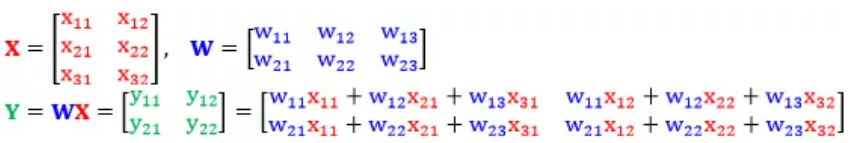
我们根据规则 $1$(形状规则),很容易知道 $frac{partial Y}{partial W}$ 的形状为 $(2,2,2,3)$,$frac{partial Y}{partial X}$ 的形状为 $(2,2,3,2)$。
误差函数 $l$ 是 Y 的标量函数,比起求 $frac{partial Y}{partial W}$ 和 $frac{partial Y}{partial X}$,我们更有兴趣求 $frac{partial l}{partial W}$ 和 $frac{partial l}{partial X}$。要推导出矩阵链式法则还需回到基本的标量链式法则。
首先关注 $frac{partial l}{partial X}$,一个个元素来看。$Y=WX$ 对应的全连接神经网络如下图(只画出一个样本)。

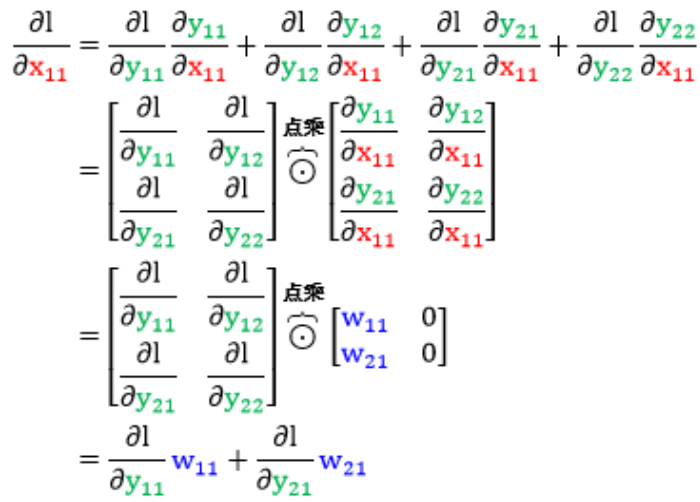

将这六项带入矩阵 $frac{partial l}{partial X}$ 整理得到
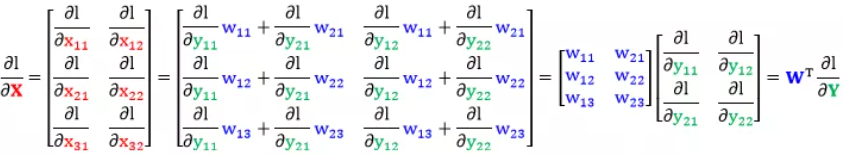
同理得到 $frac{partial l}{partial W}$

规则 $4$ 总结为:$Y, X$ 是矩阵且 $Y = WX$,$l$ 是 $Y$ 的标量函数,有 $frac{partial l}{partial W} = frac{partial l}{partial Y} cdot X^{T}$,$frac{partial l}{partial X} = W^{T} cdot frac{partial l}{partial Y}$。
5. 函数 $y = f(x)$ 都是作用在元素层面上,比如一些基本函数 $y = exp(x)$ 和 $y = sin(x)$,还有神经网络用的函数 $y = sigmod(x)$ 和 $y = relu(x)$,
它们都是标量进标量出、向量进向量出 (常见)、矩阵进矩阵出 (常见)、张量进张量出。
拿 $y = sin(x)$ 举例,整个推导可以用规则 $2$,即向量对向量求导那一套,但由于 $y$ 和 $x$ 一一对应,因此 $y$ 和 $x$ 是一样的形状,且 $y_{i}$ 只与 $x_{i}$ 有关。
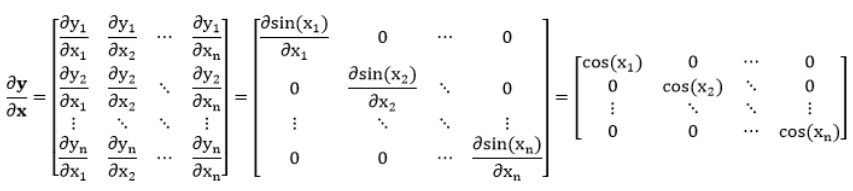
这种元素层面的函数求得的偏导数都是对角矩阵。
再次把误差函数 $l$ 请出来 ($l$ 是 $y$ 的标量函数),通常更感兴趣的是求 $frac{partial l}{partial x}$。对某个 $x_{i}$,根据链式法则得到
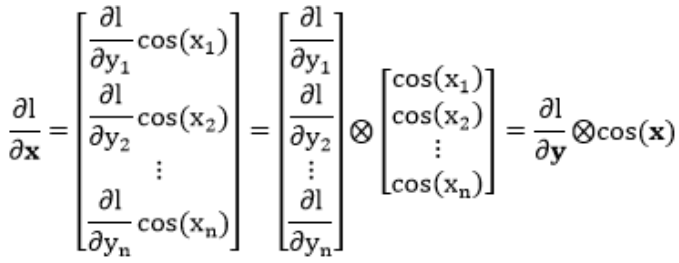
规则 $5$ 可以总结为:当函数 $y = f(x)$ 是在元素层面操作,$l$ 是 $y$ 的标量函数,有 $frac{partial l}{partial x} = frac{partial l}{partial y} otimes f^{'}(x)$。
计算图、前向传播和反向传播
先约定如下符号:惯例是用小括号 $(i)$ 上标表示第 $i$ 个数据,用中括号 $[L]$ 上标表示神经网络的第 $L$ 层。
$x = (x_{1},x_{2},...,x_{n})$:输入特征向量
$y = (y_{1},y_{2},...,y_{m})$:输出标签
$(x,y)$:单个样本点
$left { left ( x^{(1)},y^{(1)} ight ), left ( x^{(2)},y^{(2)} ight ),cdots, left ( x^{(k)},y^{(k)} ight ) ight }$:数据集,$k$ 表示数据集中样本点个数
$L = 0,1,2,...,M$:表示神经网络的第几层
$n^{[0]},n^{[1]},...,n^{[M]}$:每一层的节点个数
$W^{[1]},W^{[2]},...,W^{[M]}$:每两层之间的权重矩阵,矩阵 $W^{L}$ 的大小是 $n^{[L-1]} imes n^{[L]}$
$b^{[1]},b^{[2]},...,b^{[M]}$:每一层的偏置向量(输入层是没有偏置的)
$z^{[1]},z^{[2]},...,z^{[M]}$:每一层神经元线性求和部分的结果所组成的向量
$a^{[1]},a^{[2]},...,a^{[M]}$:每一层的输出向量
$f_{L}(z^{[L]})$:每一层的转换函数
$J$:误差函数
下面举个例子来讲述神经网络正向传播和反向传播的过程。
1. 神经网络只有单数据点 $(x, y)$,输入 $x$ 只有单特征,输出 $y$ 也只有一个标签,即 $x,y$ 都是标量
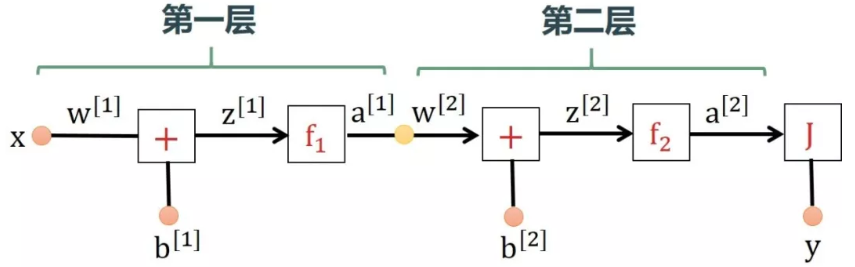
因为 $x,y$ 是标量,所以网络中的参数 $w^{[1]},b^{[1]},w^{[2]},b^{[2]}$ 和各层网络输出 $z^{[1]},a^{[1]},z^{[2]},a^{[2]}$ 都是标量。
在开始训练神经网络的时候,会随机初始化参数 $w^{[1]},b^{[1]},w^{[2]},b^{[2]}$。要利用随机梯度下降法进行参数调整,及必须知道输出 $J$
向神经网络喂一个样本点 $(x,y)$,传播过程如下:

在前向传播的过程中,每一步的计算都会利用到前面的结果,在反向传播的过程中,每一步的计算也是在已经计算的结果上进行的,也会利用到
前向传播过程中得到的数据。
以下几个量称为中间梯度:
$$frac{partial J}{partial a^{[2]}}, ;;; frac{partial J}{partial z^{[2]}}, ;;; frac{partial J}{partial a^{[1]}}, ;;; frac{partial J}{partial z^{[1]}}$$
以下几个量称为局部梯度:
$$frac{partial a^{[2]}}{partial z^{[2]}}, ;;; frac{partial z^{[2]}}{partial w^{[2]}}, ;;; frac{partial z^{[2]}}{partial b^{[2]}},
;;;;;;;; frac{partial a^{[1]}}{partial z^{[1]}}, ;;; frac{partial z^{[1]}}{partial w^{[1]}}, ;;; frac{partial z^{[1]}}{partial b^{[1]}}$$
以下几个量称为最终梯度,也是进行梯度下降法调整参数所需要的量:
$$frac{partial J}{partial w^{[1]}}, ;;; frac{partial J}{partial b^{[1]}}, ;;; frac{partial J}{partial w^{[2]}}, ;;; frac{partial J}{partial b^{[2]}}$$
了解了前向传播和反向传播的原理,下面来看一下 Pytorch 是怎么实现这个过程的。
首先来看一下 torch.Tensor 这个类的一些属性:

1)is_leaf:每一个 Tensor 都是计算图(下面介绍)中的一个节点,这个值用来表明该 Tensor 是否为叶子节点。
2)requires_grad: 用于判断该 tensor 是否需要被跟踪,用以计算梯度,默认为 False。当为 False 的时候,就意味着这个变量是不需要
计算输出(调用了 backward 的变量)关于它的导数的,在这个变量上发生的操作不会被记录,如 grad_fn 依然还是 None。或者说,这个节
点不会被加到计算图中,是游离于计算图之外的。但是如果依赖于该节点的其它张量节点的 requires_grad = True,那不管你是否设置该
值,它会自动置为 True。若没有依赖关系,那所有 requires_grad = False 的张量(Tensor)都是孤立的节点,即都为叶张量(leaf Tensor)。
3)grad:初始为 None,requires_grad = False 时为 None,否则当某 out 节点调用 out.backward() 时,会存放计算后的 $frac{partial out}{partial x}$ 梯度值,
梯度值不会自动清空,因此每次在计算 backward 时都需要将前一时刻的梯度归零,否则梯度值会一直累加。
4)grad_fn:指向用于 *Backward 函数的地址。因为叶子张量不是运算的结果,因此对应的属性 grad_fn 的值为 None,而非叶子节点是由运
算产生的,所以它会记录创建了这个 Tensor 的 Function,grad_fn 就是这个 function 的引用。举个例子:
我们首先定义一个张量 $x$,那么它是一个叶张量,对这个张量执行 $y = f(x)$,则 $y$ 是输出节点张量,函数 $f$ 定义为 $y = e^{x}$,函数 $f$ 定义如下:
class ExpBackward(torch.autograd.Function):
"""
接受一个context ctx作为第一个参数,之后传入包含输入的张量,这个函数定义 Function 的计算规则
"""
@staticmethod
def forward(ctx, i):
result = torch.exp(i)
ctx.save_for_backward(result) # 保存前向传播的计算结果 tensors,在 backward 阶段可以进行获取。
return result
"""
接受一个context ctx作为第一个参数,然后是第二个参数 grad_output,即反向传播上一次计算的梯度值,这个函数定义 Function 的求导规则
"""
@staticmethod
def backward(ctx, grad_output):
result, = ctx.saved_tensors
return grad_output * result # 在已经计算的梯度基础上再乘以局部梯度就可得到输出关于该节点的梯度。
此时输出张量 $y$ 的 grad_fn = ExpBackward。像 $+,-,/,*$ 等基本操作,Pytorch 内部都实现了对应的 Function,张量之间进行这些
操作时,也会引用对应的 Function。
在 Pytorch 和 tensorflow 中,底层结构都是由 Tensor 组成的计算图,计算图是用来描述运算的有向无环图。
下面用一个例子来说明 Pytorch 是怎么构建计算图的。
import torch a = torch.tensor(2.0, requires_grad=True) b = torch.tensor(3.0, requires_grad=True) c = a + b d = torch.tensor(4.0, requires_grad=True) e = c * d e.backward() # 执行求导 print(a.grad) # a.grad 即导数 d(e)/d(a) 的值 """ tensor(4.) """
调用 e.backward() 执行求导,为什么会更新到 a.grad?
过程是这样的:当我们执行 e.backward() 的时候。这个操作将调用 e 里面的 grad_fn 这个属性,这个属性保存的是操作函数的引用,每个
操作函数都实现了 forward 和 backward 方法,所以执行 e.backward() 后会执行 $e$ 这个张量节点所对应 Function 的 backward 方法,
Function 在前向传播中保存了输入的张量节点,所以计算出梯度后,就会将梯度值保存在对应的输入张量节点 grad 属性中,这便实现了梯度往
回传播,然后再调用输入张量节点所引用的 Function,就这样逐层往回计算,直到叶子节点......grad_fn 保存的 Function 和 Function 中保
存的输入张量都相当于图的边,反向传播就是沿着这样的路径往回走,而这个路径是前向传播过程建立的。
用圆形表示 Tensor 节点,用方形表示 Function 节点,那么这个例子在前向传播过程中建立的计算图如下:
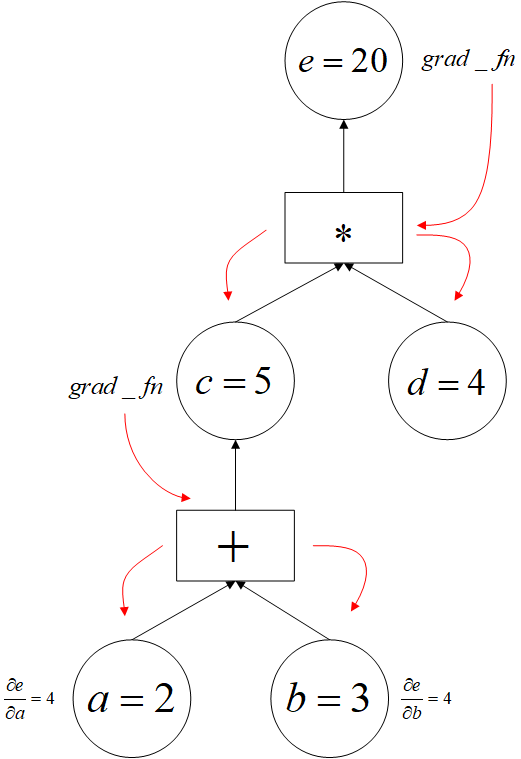
黑线代表前向传播建立动态图的过程。红线代表反向传播进行梯度计算的过程。
Function 节点不仅是沟通前向传播和反向传播的桥梁,也是沟通输入张量和输出张量的桥梁。
2. 神经网络有 $m$ 个数据点 $(X, Y)$,输入 $X$ 有多特征,输出 $Y$ 有多类别,即 $X,Y$ 都是矩阵