图像其实就是二元函数 $f(x,y)$,只不过是离散的,图像梯度就是这个二元离散函数的偏导。计算图像梯度是一个一个像素点求的。
连续二元函数的偏导数为
$$frac{partial f(x,y)}{partial x} = lim_{Delta x
ightarrow 0}frac{f(x + Delta x, y) - f(x, y)}{Delta x} \
frac{partial f(x,y)}{partial y} = lim_{Delta y
ightarrow 0}frac{f(x, y + Delta y) - f(x, y)}{Delta y}$$
但是图像是离散函数,$Delta x$ 没有办法趋于 $0$,最小只能是间隔 $1$,因此使用有限差分来近似计算梯度。因此,图像偏导变成了如下形式:
$$frac{partial f(x,y)}{partial x} = f(x + 1, y) - f(x, y) \
frac{partial f(x,y)}{partial y} = f(x, y + 1) - f(x, y)$$
$x,y$ 表示某个像素的坐标,除了上面这个前向差商外,还可以采用后向差商,中心差商来计算梯度。比如采用中心差商:
$$frac{partial f(x,y)}{partial x} = frac{f(x + 1, y) - f(x - 1, y)}{2} \
frac{partial f(x,y)}{partial y} = frac{f(x, y + 1) - f(x, y - 1)}{2}$$
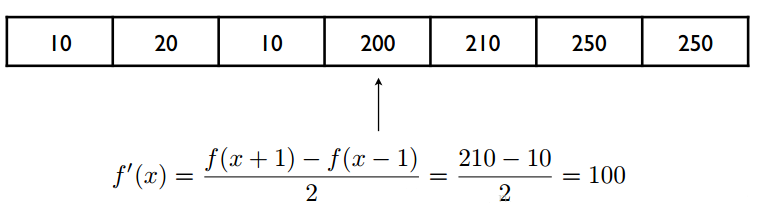
写成一维卷积的形式等于与 $[-1, 0, 1]$ 这样一个滤波核作卷积。
对于离散的图像来说,一阶微分的数学表达相当于两个相邻像素的差值,根据选择的梯度算子不同,效果可能有所不同,但是基本原理不会变化。
比如 sobel 算子也可以计算梯度,本质也是通过差分计算,但是用到了前后向序列的信息,同时为每个元素附加权重。

