实 验 报 告
课程:程序设计与数据结构
姓名:杨京典
班级:1623
学号:20162302
实验名称:图的实现与应用
实验器材:装有IdeaU的联想拯救者15ISK
实验目的与要求:
1.用邻接矩阵实现无向图
2.用十字链表实现无向图
3.实现PP19.9
实验内容、步骤与体会:
实验内容:
完用邻接矩阵实现无向图
AdjMatrixGraph
用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
- 顶点类
Vertex:图由顶点和边两种要素构成,在邻接矩阵实现的无向图里面边由一个矩阵就可以表示出由某一顶点指向的另一个顶点的边是否存在以及这条边的长度,而顶点需要单独一个类来盛放这个顶点的相关属性。

其中要有它所盛放的数据以及它是否被访问过两种基本属性。可以根据情况写出方法来更改它的数据,访问它,以及给出打印时候的格式。不考虑封装的话可以直接将wasVisited变成公共的。
public class Vertex<T> {
private Comparable data;
public boolean wasVisited;
public Vertex(Comparable data){
this.data = data;
wasVisited = false;
}
public void setData(Comparable a){
data = a;
}
public String toString(){
return data+"";
}
}
- 添加边
setLine()和删除边的removeLine()方法:在AdjMatrixGraph里面边被都在在一个二维数组里面所以再添加和删除的时候就可以直接对这个数组进行操作。因为是无向图,所以再添加和删除的时候要处理两个方向的操作。
public void addLines(int a, int b, int weigt) {
if (lines[a][b] != 0)
System.out.println("The line has been set!");
lines[a][b] = weigt;
lines[b][a] = weigt;
}
public void removeLines(int a, int b) {
if (lines[a][b] == 0)
System.out.println("The line has been remove!");
lines[a][b] = 0;
lines[b][a] = 0;
}
- 添加顶点的
setVertex()方法和删除顶点的removeVertex()方法
添加顶点的setVertex()方法和删除顾点的remoeVertex0方法: 添加顶点的方法比较简单,直接在数组里面放入一个新的顶点即可。
在删除顶点的时候首先要考虑到删除的顶点是否存在,然后执行两个动作一是要把与它相连的边删除,二是要把与它后面的数据移动位置。
首先是对于异常情况的处理,当删除不存在的顶点的时候可以抛出异常,也可以使用f判断语句来避免异常代码的执行
if (a > count)
System.out.println("We don't have enough data");
else {};
然后就是从数组中删除顶点,共有两种方案,一种是给要删除的数据赋值为null,并使用删除方法删除与其相邻的所有边。但是这种方法会造成空间的浪费,所以在代码优化的时候使用了第二种思路:
1、使用一个循环删除指定顶点,并把后面的顶点向前移动
for (int i = a; i<count;i++)
vertex[i-1]=vertex[i];
2、假设删除的数据是第二十个数据,删除后的数据的边的矩阵可以分为ABCD四个模块,由被删除的数据隔开
在删除以后,需要将B区的数据向左移
for(int j=0;j<a;j++)
for(int k=a+1;k<count;k++)
lines[j][k-1] = lines[j][k];
C区的数据向上移
for(int j=a+1;j<count;j++)
for(int k=0;k<a;k++)
lines[j-1][k] = lines[j][k];
D区的数据向左上移
for(int j=a+1;j<count;j++)
for(int k=a+1;k<count;k++)
lines[j-1][k-1] = lines[j][k];
size()方法和isEmpty()方法:这两个方法就很简单了,一个返回计数变量,一个判断是否为空
public boolean isEmpty() {
return count == 0;
}
public int size() {
return count;
}
- 广度优先迭代器:广度优先是从一个顶点开始,辐射状地优先遍历其周围较广的区域,故称之为广度优先遍历。

实现思路:需要一个队列来保存遍历过的顶点顺序,以便按出队的顺序再去访问这些顶点的邻接顶点。
//广度优先,纯天然打造绿色无污染
public Stack breadthFirstSearch(int i){
if (!vertex[i].wasVisited) {
//判断节点是否被访问过,若未被访问,则访问并压入栈
stack.push(vertex[i]);
vertex[i].wasVisited = true;
}
while (visited()) {
for (int j = 0; j < count; j++)
//扫描与节点相邻的所有节点,并将扫面到的节点访问并压入栈
if (lines[i][j] != 0 && !vertex[j].wasVisited) {
que.enqueue(j);
//将序号压入队列
stack.push(vertex[j]);
//将数据压入栈
vertex[j].wasVisited = true;
}
if(que.isEmpty())
break;
breadthFirstSearch(que.dequeue());
//扫描完成后从队列弹出最先压入队列的序号并从这个序号开始扫描
}
return stack;
}
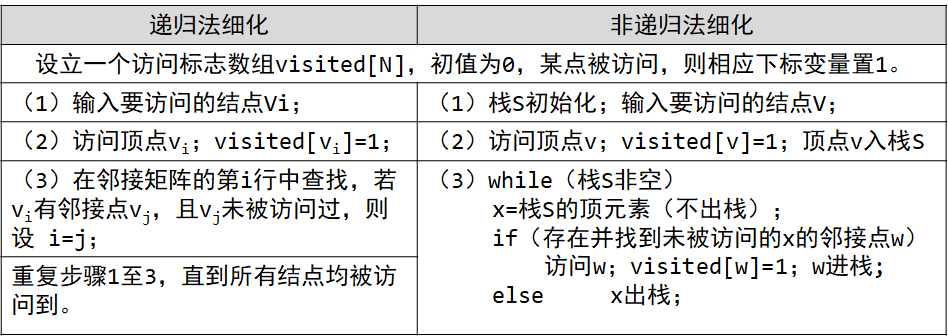
- 深度优先迭代器:图的深度优先搜索,类似于树的先序遍历,所遵循的搜索策略是尽可能“深”地搜索图。如果它还有以此为起点而未探测到的边,就沿此边继续探寻下去。一直进行到已发现从源节点可达的所有节点为止。
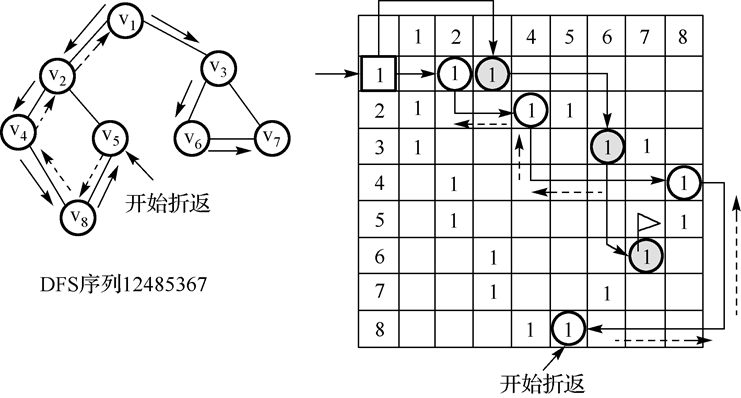
实现思路:
//深度优先,纯手工打造绿色无污染
public Stack depthFirstSearch(int i) {
//输入要访问的结点
stack.push(vertex[i]);
//将访问的节点压入栈
vertex[i].wasVisited = true;
//访问顶点
while (visited()) {
for (int j = 0; j < count; j++) {
if (lines[i][j] != 0 && !vertex[j].wasVisited) {
//在邻接矩阵的第i行中查找,若vi有邻接点vj,且vj未被访问过,则设 i=j;
i = j;
depthFirstSearch(i);
} else {
for(int x = 0; x<count;x++)
//若找不到相邻的节点则寻找未被访问过的节点并访问
if (!vertex[x].wasVisited)
depthFirstSearch(x);
}
}
}
return stack;
}
用十字链表实现无向图
CrossGraph
用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),,sEmpty(),广度优先迭代器,深度优先迭代器
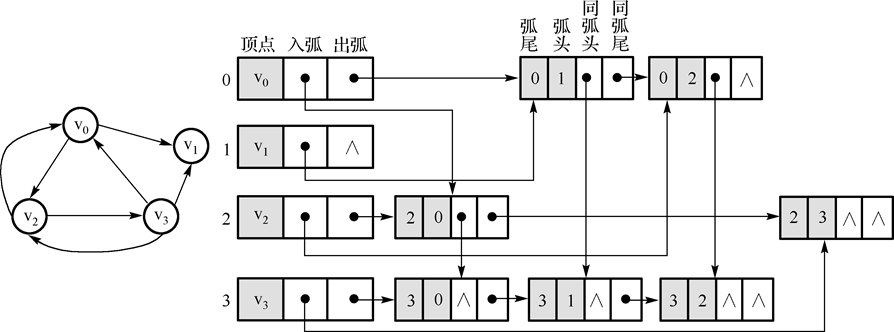
- 首先是顶点类和边类:顶的结构包含,它的数据,入弧,出弧和访问状态。为了方便访问,我设置了一个指针指向它连接的最后一条弧和指向它的最后一条弧。同时在复写
toString()的的时候不能引用null值,所以要加个判断语句。
public class VertexC<T> {
T data;
LineC<T> firstIn;
LineC<T> firstOut;
LineC<T> lastIn;
LineC<T> lastOut;
public boolean wasVisited;
public VertexC(T data) {
firstIn=null;
firstOut=null;
lastIn = null;
lastOut = null;
wasVisited = false;
this.data = data;
}
public String toString(){
String result="";
if (firstIn!=null&&firstOut!=null)
result = "[" + data + ", 入弧" + firstIn.name + ", 出弧" + firstOut.name + "]";
if (firstIn==null&&firstOut!=null)
result = "[" + data + ", " + "null" + ", " + firstOut.name + "]";
if (firstIn!=null&&firstOut==null)
result = "[" + data + ", " + firstIn.name + ", " + "null" + "]";
return result;
}
}
图中边的类包含弧头、弧尾、同弧头、同弧尾、四个属性
public class LineC<T> {
String name = "line";
int fromVertexIndex;
int toVertexIndex;
LineC<T> nextSameFromVertex=null;
LineC<T> nextSameToVertex=null;
public LineC(int name, int fromVertexIndex, int toVertexIndex) {
this.name += name;
this.fromVertexIndex = fromVertexIndex;
this.toVertexIndex = toVertexIndex;
}
public String toString(){
String result="";
if (nextSameFromVertex==null&&nextSameToVertex!=null)
result = "[" + name + ": 弧尾" + fromVertexIndex + ", 弧头" + toVertexIndex + ", 同弧头" + "null" + ", 同弧尾" + nextSameToVertex.name + "]";
if (nextSameFromVertex!=null&&nextSameToVertex==null)
result = "[" + name + ": 弧尾" + fromVertexIndex + ", 弧头" + toVertexIndex + ", 同弧头" + nextSameFromVertex.name + ", 同弧尾" + "null" + "]";
if (nextSameFromVertex!=null&&nextSameToVertex!=null)
result = "[" + name + ": 弧尾" + fromVertexIndex + ", 弧头" + toVertexIndex + ", 同弧头" + nextSameFromVertex.name + ", 同弧尾" + nextSameToVertex.name + "]";
return result;
}
}
直接进行无向连接判断思路有些复杂,但是可以看做来回的两次有相连接。在设置连接关系的时候要判断两个点分别是否有入弧和出弧,所以要写出四种不同的情况。
public void addLines(int a, int b) {
addLine(a, b);
addLine(b, a);
}
private void addLine(int a, int b) {
line[countL] = new LineC(countL, a, b);
if (vertex[a].firstOut == null) {
vertex[a].firstOut = line[countL];
vertex[a].lastOut = line[countL];
} else {
vertex[a].lastOut.nextSameFromVertex = line[countL];
vertex[a].lastOut = line[countL];
}
if (vertex[b].firstIn == null) {
vertex[b].firstIn = line[countL];
vertex[b].lastIn = line[countL];
} else {
vertex[b].lastIn.nextSameToVertex = line[countL];
vertex[b].lastIn = line[countL];
}
countL++;
}
- size(),,sEmpty(),广度优先迭代器,深度优先迭代器都和邻接矩阵实现图的方法一样,这里就不赘述了。
实现PP19.9
ComputerInternet
创建计算机网络路由系统,输入网络中点到点的线路,以及每条线路使用的费用,系统输出网络中各点之间最便宜的路径,指出不相通的所有位置。
- 对于这一程序的实现,可以继承无向图,也可以调用无向图,调用的话可以通过如下方法实现。
public void addVertex(){
count++;
adjMatrixGraph.addVertex("Computer:" + count);
}
public void addLine(int a, int b, int cost){
adjMatrixGraph.addLines(a,b,cost);
}
- 在判断最短路径的时候可以使用Dijkstra方法
实现思路:(1)在Dist中找最小值对应的点u;将u加入S。
(2)以u做中间点,分别计算源点v0到其他各顶点的距离;若小于原来的距离,则修改Dist和Path数组。
具体到数据结构,则可表述为:
如果Dist[x]>Dist[u]+AdjMatrix[u][x],则Dist[x]=Dist[u]+AdjMatrix[u][x]。
(3)重复步骤(1)(2)直到所有与v0有路径的顶点全部都加入到S中。
public int dijkstra(int a, int b){
int[][] adjMatrix = adjMatrixGraph.datas();
int u = 0;
for (int i = 0; i<count;i++)
if (adjMatrix[a][i]==0)
dist[i]=9999;
else dist[i]=adjMatrix[a][i];
//在Dist中找最小值对应的点u;将u加入S。
while (count1 != count) {
for (int i = 0; i < count; i++)
if (dist[i] < dist[u])
u = i;
S[count1++] = dist[u];
//以u做中间点,分别计算源点v0到其他各顶点的距离;若小于原来的距离,则修改Dist和Path数组。
for (int x = 0; x < count; x++)
if (dist[x] > dist[u] + adjMatrix[u][x])
dist[x] = dist[u] + adjMatrix[u][x];
}
//具体到数据结构,则可表述为:
//如果Dist[x]>Dist[u]+AdjMatrix[u][x],则Dist[x]=Dist[u]+AdjMatrix[u][x]。
//重复步骤(1)(2)直到所有与v0有路径的顶点全部都加入到S中。
return dist[b];
}