一、泛化
官方定义
在周老师的《机器学习》一书 (P3) 中,泛化能力一词定义如下:
学得模型适用于新样本的能力,称为 “泛化”(generalization)能力。
同理,泛化误差的存在就是为了防止学习器把训练样本学得太好了,导致可能已经把训练样本自身的一些特点当做了所有潜在样本都会具有的一般性质。
缺陷
因为泛化性能是建立在 主观臆测 的沙雕之上,只是一种 对个人假想的“实际情况”的模拟 。因此,没有人能对 尚未出现的新样本 的 分布特点 做出保证正确的限定。
“泛化”是任人打扮的小姑娘
具体举例,比如有些解决不平衡样本的方法,是通过加大对量少类别样本的采样来提高模型的泛化性能的。
在测试样本中,如果 新样本的 分布特点 是 各类样本数量均衡,那么上述解决方法当然是行之有效的。
但是如果 新样本的 分布特点 符合马太效应而多者愈多呢?那么上述解决方法似乎就 与 新定义的“泛化” 背道而驰了。
反之亦然。
二、细化
图像细化(Image Thinning),一般指二值图像的骨架化(Image Skeletonization) 的一种操作运算。
细化是将图像的线条从多像素宽度减少到单位像素宽度过程的简称,一些文章经常将细化结果描述为“骨架化”、“中轴转换”和“对称轴转换”。
用骨架来表示线划图像能够有效地减少数据量,减少图像的存储难度和识别难度。
思考
1、为什么激活函数使用非线性?
例子:
如一个图像特征:(0、1代表黑白色度)
1 0 1
0 0 0
1 0 1
若提取特征为
1 0 0
0 0 0
1 0 0
其基本特征基本没有用,偏向于随机性,但是若使用的激活函数为线性的,则这第二幅图的得分是全特征得分的一半,这很不合理
提取到的特征越接近原来所需要的特征得分越高,故而非线性如sigmoid函数更加符合这样子的特性
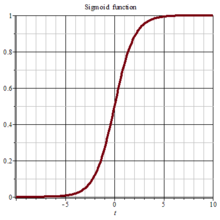
越接近所需特征,其得分应该是指数型增长
2、 泛化 ------> 或关系
细化 ------> 与关系
还是上面的例子:
如一个图像特征:(0、1代表黑白色度)
1 0 1
0 0 0
1 0 1
若设置b为3,则提取到特征为
1 0 0 1 0 1 1 0 1 0 0 1 1 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 1 0 0 0 0 1 1 0 1 1 0 1
可认为接近所需提取的特征,即上面三种情况之一都可以
即: (A&B&C)
|(A&C&D)
|(B&C&D)
|(A&B&D)
|(A&B&C&D)//ABCD分别代表四个点
故而满足三个点及以上(满足b),则可认为提取到特征了。同时满足符合特征规则的为与关系,但任一满足一种都可以的为或关系,即模型学会判断是否为这些其中之一
所以激活函数如relu,sigmoid都满足的条件有:
1、 非线性 (必须达到的条件,与条件)
2、 或关系,泛化
3、为什么神经网络一定要深层化?
比如一个树形的特征图像
我们需要提取的特征为左边五个点的树形图像,怎么将其筛选出来呢?(即提取标准为5个)
可以先进行收缩

这是腐蚀第一次
这是腐蚀第二次,图层只剩下目标的一个点
这时对齐膨胀两次,既可以得到所需的特征

这样子就经过了四层(两层腐蚀层,两层膨胀层)
对于一个简单的问题处理,就需要四层,当我们在处理一个复杂的事物的时候,需要进行多步的剖析和处理,这样子就需要多层网络,当然,多层网络可以使得参数变少
例如:为什么使用两个3*3的卷积代替一个5*5的卷积?
原因:通过数学的论证,可以发现3*3的卷积是将两个长的卷积拆成了一个多项式和一个卷积的和