最近开始学习Coursera上的斯坦福机器学习视频,我是刚刚接触机器学习,对此比较感兴趣;准备将我的学习笔记写下来,
作为我每天学习的签到吧,也希望和各位朋友交流学习。
这一系列的博客,我会不定期的更新,希望大家多多批评指正。
Supervised Learning(监督学习)
在监督学习中,我们的数据集包括了算法的输出结果,比如具体的类别(分类问题)或数值(回归问题),输入和输出存在某种对应关系。
监督学习大致可分为回归(classification)和分类(regression)。
回归:对于连续型数值的预测;
分类:对于离散输出的预测,输出为某些具体的类别;
Unsupervised Learning(无监督学习)
在无监督学习中,我们对于输出的结果一无所知,根据数据的内在结构将数据聚类,我们无法得到预测结果的反馈。
总结:监督学习和无监督学习的重要区别,数据集的输出结果是否事先知道。
课程pdf:https://www.coursera.org/learn/machine-learning/supplement/d5Pt1/lecture-slides
Model Representation(模型表示)
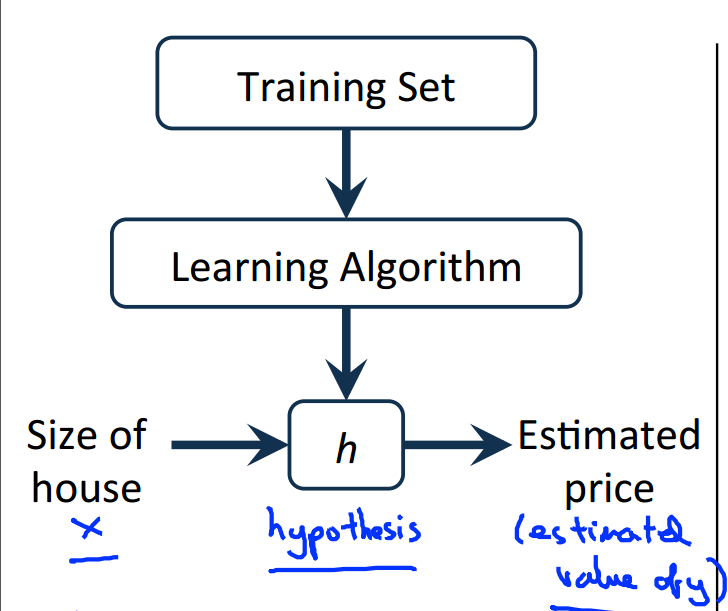
以上是监督学习问题的图示描述,我们的目标是,给定训练集,学习函数h:X→Y,使得h(x)是对于y有较好的预测值。
h(x)代表的是一个假设集合(Hypothesis ),我们要做的就是从这个假设集合中找出预测效果最好的那一个假设。

下面是后文将用到的符号表示,请务必明白其表示的意思,这个不难。

Cost Function(损失函数)
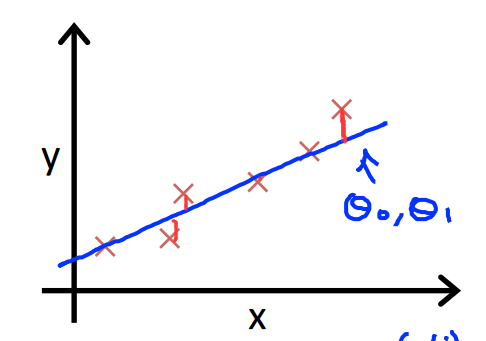
之前举的例子,关于房价的预测问题,是一个单变量的回归问题,输入数据只有x维度为1,
我们建立的模型是![]() ,我们的目标是让这个直线尽可能的拟合所有数据,
,我们的目标是让这个直线尽可能的拟合所有数据,
即从数据的中心穿过,让我们的每个预测值h(x)与我们的已知数值y尽可能的接近。
那么,我们应该怎么选择最好的模型呢?通过求解参数theta1和theta2.
我们可以通过使用 cost function(损失函数)来测量我们的假设的准确性。 这需要使用来自x的输入
和实际输出y的假设的所有结果的平均差(实际上是平均值的更好的版本),如下。
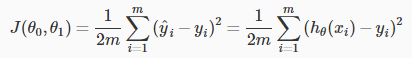
说明:其实损失函数 J 计算的是h(x)与真实值y之间的垂直距离的平方和均值。
关于为什么多一个1/2的问题,是为了以后求导方便,不用太在意这个。

为了问题描述的方便,首先使用上图右边的简单模型,只有一个参数theta1.
下图是对数据样本点”X“的拟合状态,
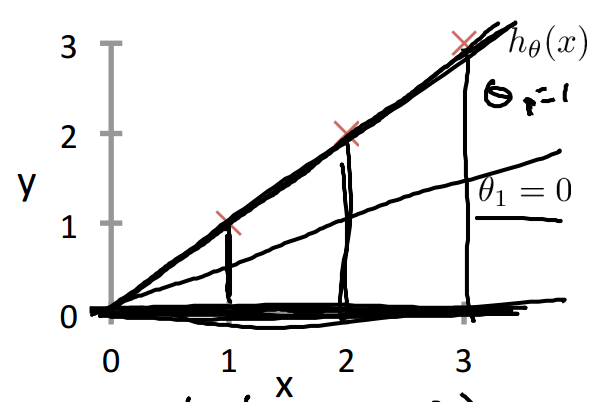
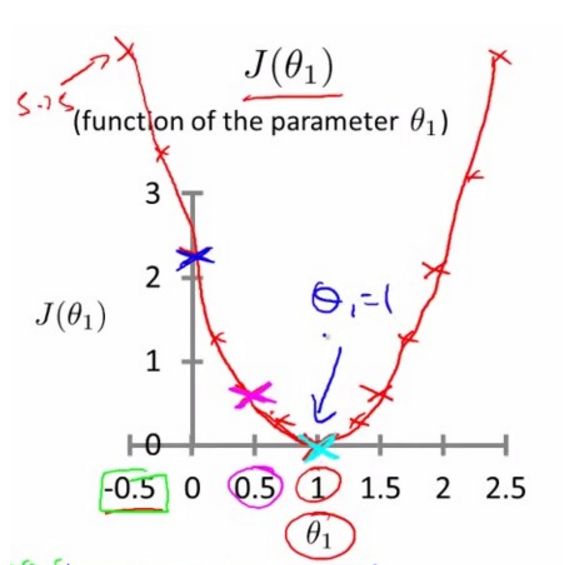
当在上图中我们随意旋转h(x),将会得到不同的 J 值,可以得到下面的关于theta1 损失函数 J 的图像:
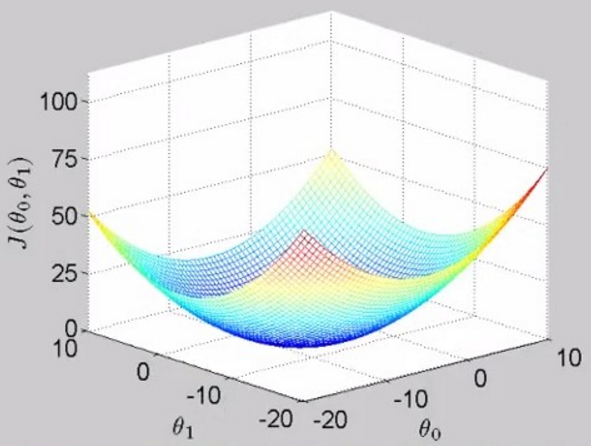
当同时考虑两个参数值 theta1和theta0时,损失函数的图像是这样的,被称为bowl-shape function,碗状的
下图的右边是上面三维图像的二维展示,那一圈一圈的椭圆被称为“等高线”(类似地理上的等高线),每一个椭圆上的不同点的 J 值都是相等的,
如图中绿色椭圆上的三个点,越靠近中心的椭圆 J 值越小。
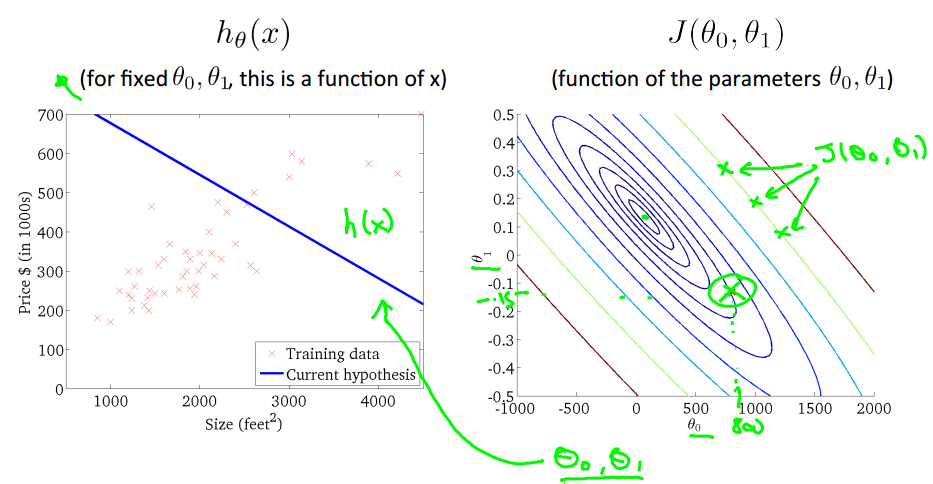
上面左图对应的是右图中用绿色圆圈标注的点(theta1=800,theta0=-1.5),对应的模型h(x)的图像,右图中每一个不同的点,
都会在左图中对应一个不同的图像,如下:
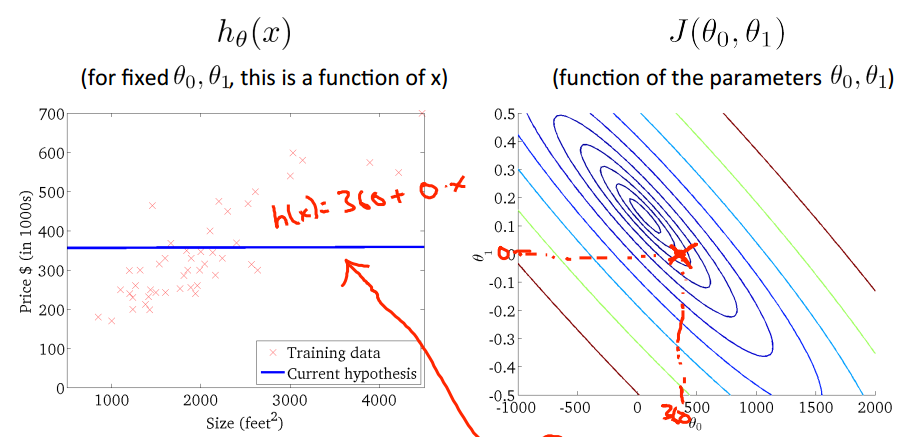
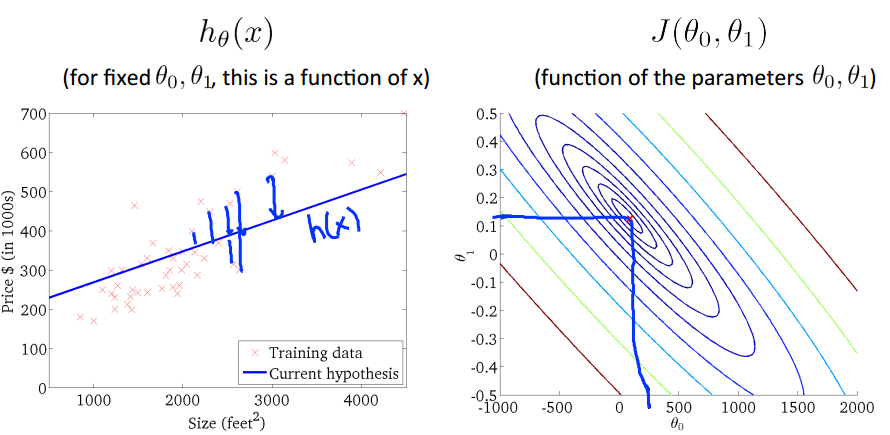
当然,我们理想的情况是类似上图的情况,我们取的(theta1,theta0)出现图中的中心theta0=450,theta1=0.12,
在这个点可以是损失函数达到最小,趋近于0.这样我们就求得了模型参数theta0和theta1,进而得到最佳的假设h(x)。
Gradient Descent(梯度下降)
我们有了假设模型h(x),和损失函数 J,现在来讨论如何求得theta1和theta0的方法,梯度下降。我们的问题描述如下:

需要不断迭代,求得使损失函数 J 达到最小的theta1和theta0.
关于梯度下降的理解:
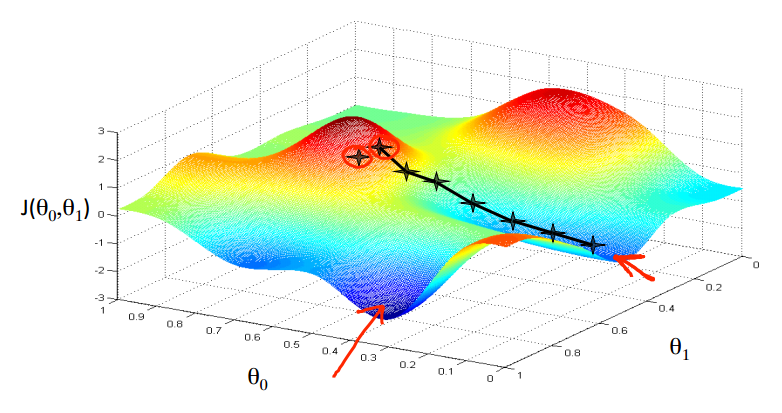
假设你现在站在两座山包上的其中一座,你需要以最快的速度下到山的最低处。每到达一个新的地方,
都选择在该点处梯度最大的方向下山即可。如图:
梯度下降算法表示如下:其中标出了梯度(蓝框内)和学习率(α > 0),梯度在这里通俗的说就是函数 J 的偏导数。
注意:梯度下降算法对局部最小值敏感,梯度下降可能收敛在局部最小,不能保证收敛到全局最小值。

说明:在计算机科学中,x:=x+y表示,先计算x+y的结果再赋值给变量x,类似先计算a=x+y,然后使x的值等于a。
下图为梯度为正、负的情况,theta的更新是不一样的:
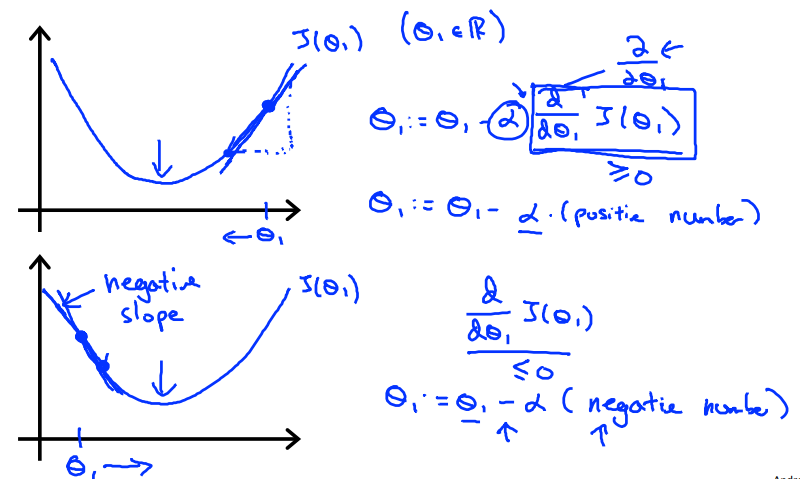
关于参数更新的问题,theta1和theta2必须同时更新,下图左边为正解,即不能使用更新过后的theta0来进一步更新theta1
(这将是后面要讲到了另一种算法)。

关于学习率α的问题:
当a过小的时候,迭代步长太小,梯度下降得太慢;
当a过大的时候,迭代步长过大,梯度无法收敛到最小值,而发生左右震荡的现象。
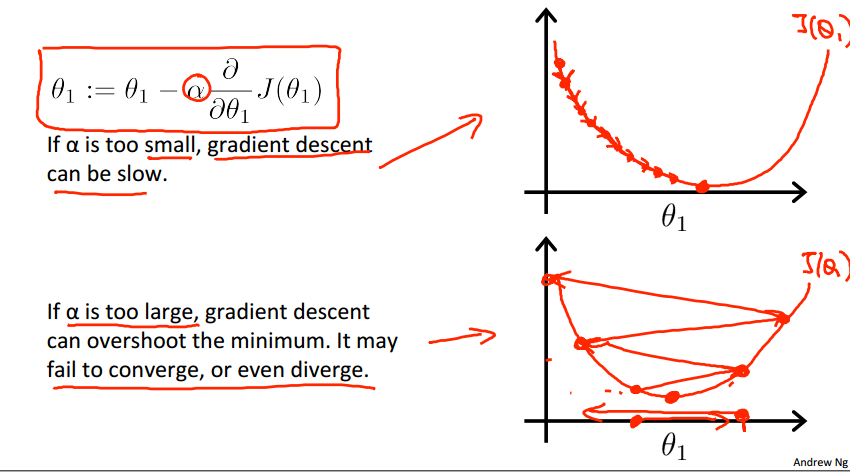
当固定a时,梯度下降法依然可以收敛到最小值(局部),
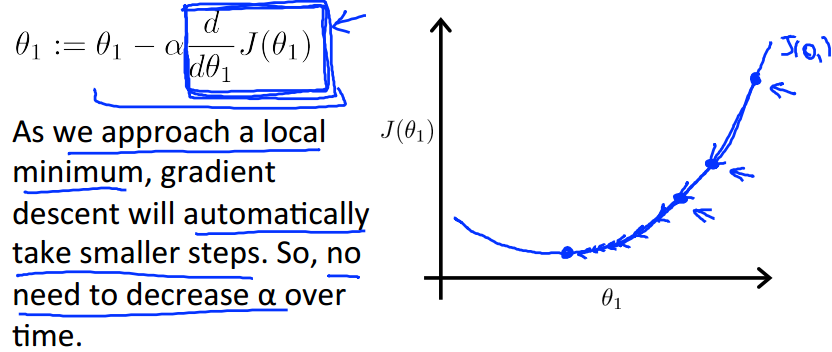
因为,当我们越靠近最小值时,我们的 梯度 越小,反应在上图就是越来越平缓,所以上面蓝色方框中的表达式会越来越小,
然后乘上a也越来越小,证明我们迭代的步长会逐步变小,即使我们使用的是固定不变的学习率a。
Gradient Descent For Linear Regression
(在线性回归中使用梯度下降)

其推导过程如下,分别对 J 求 关于theta0和theta1的偏导数:
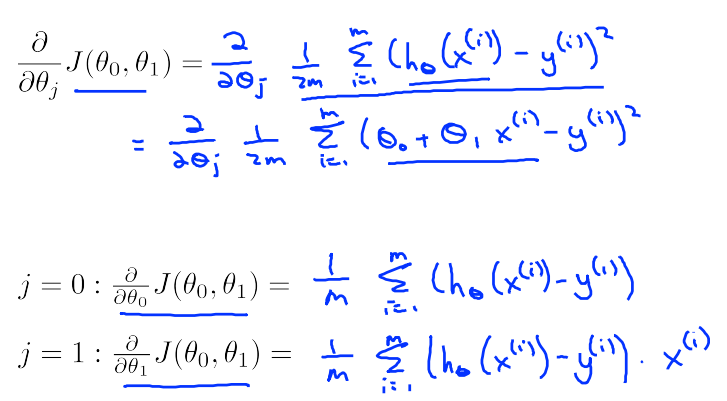
得到下面应用于线性回归的梯度下降算法:

通过对以上算法的不断迭代,我们求得了最好的假设h(x),其中红色“x”的轨迹,就是算法迭代的过程。

注:上面提到的梯度下降算法叫做“Batch” Gradient Descent,批梯度下降算法(翻译可能有所不同),其每一次迭代都需要使用整个数据集,
所以其效率不高,后面会学习到它的改进算法,随机梯度下降。
参考文献:http://blog.csdn.net/abcjennifer/article/details/7691571