n阶行列式的行数和列数相等,都为n。
二阶行列式,

三阶行列式,

对角线法则只适用于二阶与三阶行列式,为研究四阶及更高阶行列式,下面先介绍有关全排列的知识,然后引出n 阶行列式的概念.
排列及其逆序数,

逆序数,

对换,

3. n阶行列式的定义
为了给出n 阶行列式的定义,先来研究三阶行列式的结构. 三阶行列式定义为

仿此,可以把行列式推广到一般情形。


上/下三角行列式和对角行列式的结果都为主对角线的乘积。
4. 行列式的性质
转置行列式,沿着主对角线对折。

性质1 行列式与它的转置行列式相等.
性质2 对换行列式的两行(列),行列式变号. 【下面是第1行和第3行对换的示例】

推论 如果行列式有两行(列)完全相同,则此行列式等于零.
性质3【乘法】 行列式的某一行(列)中所有的元素都乘同一数k,等于用数k 乘此行列式.【很明显,计算行列式的每个数值都是从每行/列取出来的元的乘积a1p1a2p2a2p3】
推论 行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面.
性质4 行列式中如果有两行(列)元素成比例,则此行列式等于零.【把这个比例提到行列式记号外面,就有两行/列完全相同,根据性质2的推论,可得此行列式为零】
性质5【加法】 若行列式的某一行(列)的元素都是两数之和,例如第i 行的元素都是两数之和:

【每行/列的元都参与乘积运算,可以根据乘法的结合律拆分】
性质6 把行列式的某一行(列)的各元素乘同一数然后加到另一行(列)对应的元素上去,行列式不变.【根据性质5可以把右边的行列式拆分成两个之和,其中一个就是左边的行列式,另一个行列式,根据性质3的推论,可以把k提到行列式记号外面,就得到一个有两行/列相同的行列式,根据性质2的推论,该行列式为零】

后面的性质都是从前面的性质推导出来的,可以有很多。
例题,

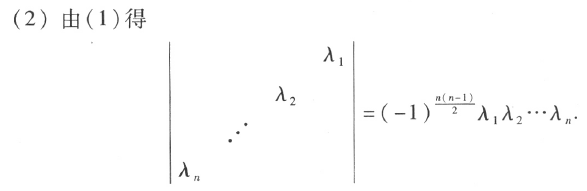
对于求行列式而言,最重要的是性质6。
例7,
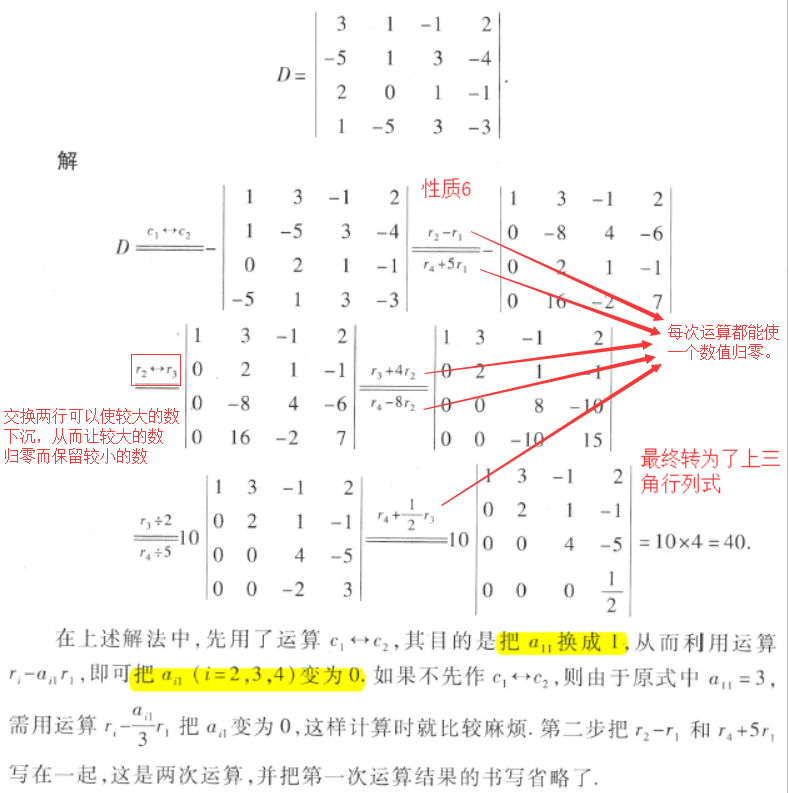


上述诸例都是利用运算ri + k*rj 把行列式化为上三角形行列式,用归纳法不难证明(这里不证)任何n 阶行列式总能利用运算ri + k*rj 化为上三角形行列式,或化为下三角形行列式(这时要先把a1n,…,an-,1 n化为0).类似地,利用列运算ci + k*cj,也可把行列式化为上三角形行列式或下三角形行列式.

例11,
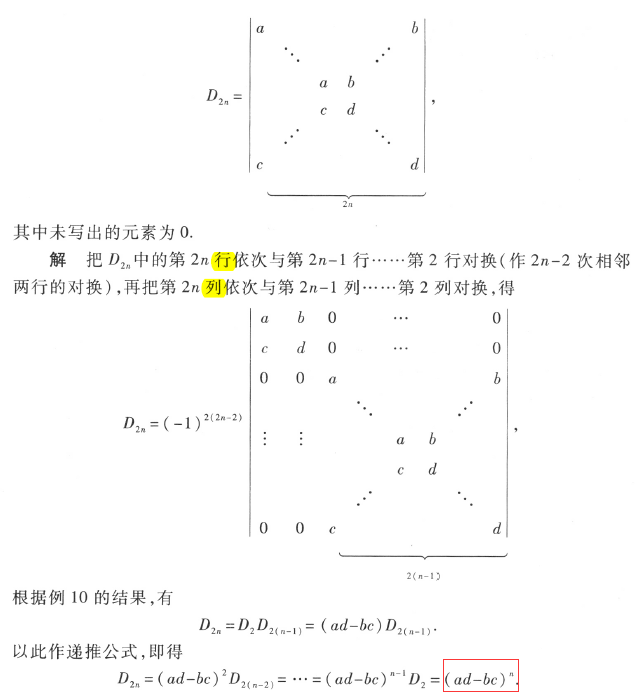
5. 行列式按行/列展开
一般说来,低阶行列式的计算比高阶行列式的计算要简便,于是,我们自然地考虑用低阶行列式来表示高阶行列式的问题.为此,先引进余子式和代数余子式的概念.

注意:M就是行列式,是一个数值。A是从M的基础上得到的。






例13,。。。