矩阵

重要公式：

矩阵的转置，

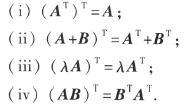        分别对应矩阵的三种运算。

方阵的行列式，只有方阵才有行列式，设A、B为n阶方阵，

       

伴随矩阵，

        AA* = A*A = |A| E

逆矩阵，从逆矩阵的定义来看，A、B都是n阶方阵，并且是可交换的。

       

       

       

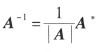
一般来说AB≠BA，但总有|AB| = |BA|

矩阵和行列式的区别，行列式的标识是竖杠，矩阵的标识是括弧。

下面是栽过的坑，把矩阵当作行列式了。。。涉及的知识点是数与矩阵相乘。

三条定理：

1. AB互为逆矩阵。

2. 若A是可逆的，则A的逆矩阵是唯一的。

3. 判定矩阵不可逆。

性质：

 

1. 可逆矩阵一定是方阵。

2. A的逆矩阵的逆矩阵还是A。记作（A^-1）^-1=A。

3. A的转置矩阵A^T也可逆，并且（A^T）^-1=（A^-1）^T (转置的逆等于逆的转置）

4. 若矩阵A可逆，则矩阵A满足消去律。即AB=O（或BA=O），则B=O，AB=AC（或BA=CA），则B=C。

5. 两个可逆矩阵的乘积依然可逆。

6. 矩阵可逆当且仅当它是满秩矩阵。

 

满秩矩阵

 

矩阵的阶：行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵，n阶矩阵A也记作A_n.

两个矩阵的行数、列数都相等时，就称它们是同型矩阵。如果A=(a_ij)与B=(b_ij)是同型矩阵，并且它们的对应元素相等，即 a_ij = b_ij （i= 1， 2，…，m； j= 1，2，…，n），那么就称矩阵A与矩阵B相等，记作A = B。

元素都是零的矩阵称为零矩阵，记作O。

-A称为矩阵A的负矩阵，显然有A+(-A)=O。

 

1. 线性方程组和矩阵

线性方程组，

矩阵的定义，

特别特别需要注意的是：矩阵和行列式的区别，行列式的标识是竖杠，矩阵的标识是括弧。

向量的概念就是这么来的啊！

同型矩阵：即shape相同。

线性变换，

对角矩阵，恒等变换，n阶单位矩阵

由于矩阵和线性变换之间存在一一对应的关系，因此可以利用矩阵来研究线性变换，也可以利用线性变换来解释矩阵的含义。

2. 矩阵的运算

矩阵的加法，

数与矩阵相乘，

矩阵加法与数乘矩阵统称为矩阵的线性运算。

矩阵与矩阵相乘，

矩阵乘法满足结合律和分配律，但不满足交换律。

对角阵，恒等变换，单位矩阵，纯量阵。

只有当AB可交换时，上面的结论才成立。

 矩阵的转置，

注意第4条，A、B的顺序变了。

对称阵，

方阵的行列式，

定义6 由n阶方阵A的元素所构成的行列式(各元素的位置不变)，称为方阵A的行列式，记作det A或|A|.

第3条规律在证明 “可逆矩阵的行列式非零” 时用到了。

伴随矩阵，

矩阵A与其伴随矩阵A^*是可交换的。

伴随矩阵实例1，

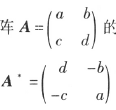
伴随矩阵实例2，

求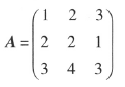的伴随矩阵

注意：不要忘记(-1)^i+j。

3. 逆矩阵

注意：从逆矩阵的定义来看，A、B都是n阶方阵，并且是可交换的。

奇异矩阵：|A| = 0。

 

注意：第3条中的'-1'是逆，不是幂。

逆矩阵的初步应用，

矩阵A的m次多项式，

4. 克拉默法则

求解由n 个n 元线性方程组成的方程组。

例题，分别用克拉默法则和逆矩阵方法求解

5. 矩阵分块法

分块矩阵，

分块矩阵的运算规则，

只有一个元素的矩阵，其伴随矩阵是1吧。

今后列向量（列矩阵）常用小写黑体字母表示，如a、α、x 等，而行向量（行矩阵）则用列向量的转置表示，如a^T、α^T、x^T等.

例19先剩着。。。