第五章 栈和队列
在常用的数据结构中,有一批结构被称为容器。一个容器结构里总包含一组其他类型的数据对象,称为元素,容器支持对这些元素的存储、管理和使用。一组容器具有相同性质,支持同一组操作,可以被定义为一个抽象数据类型。
线性表就是一类容器,该类数据对象除了可以保存元素,支持元素访问和删除外,还记录了元素之间的一种顺序关系。
另外两类最常用的容器是栈(stack)和队列(queue),它们都是使用最广泛的基本数据结构。
5.1 概述
栈和队列主要用于在计算过程中保存临时数据,这些数据是计算中发现或产生的,在后续的计算中可能需要使用它们。如果可能生成的数据项数在编程时就可确定,问题比较简单,可以设置几个变量作为临时存储。但如果需要存储的数据项数不能事先确定,就必须采用更复杂的机制存储和管理,这种机制被称为缓冲存储或缓存。栈和队列就是使用最多的缓冲存储结构。
5.1.1 栈、队列和数据使用顺序

在计算中,中间数据对象的生成有早有晚,存在时间上的先后顺序。在后续使用这些元素时,也可能需要考虑它们生成的时间顺序。最典型的两种顺序是:先进先出和后进先出。
从实现的角度看,应该考虑最简单而且自然的技术。由于计算机存储器的特点,要实现栈或队列,最自然的技术就是用元素存储的顺序表示它们的时间顺序。也就是说,应该使用线性表作为栈和队列的实现结构。
5.1.2 应用环境

可直接使用list实现栈的功能。python标准库提供了一种支持队列用途的结构deque。
5.2 栈:概念和实现
存入栈中的元素之间没有任何具体关系,只有到来的时间先后顺序。栈的基本性质保证了,在任何时刻可以访问、删除的元素都是在此之前最后存入的那个元素,因此,栈确定了一种默认元素访问顺序。
5.2.1 栈抽象数据类型
栈的基本操作是一个封闭的集合(与线性表的情况不同)。下面是一个栈的抽象数据类型描述,其中定义的操作包括:栈的创建、判断栈是否为空、入栈、出栈、访问最后入栈元素(不删除)。最后两个操作都遵循LIFO原则。另外,对这两个操作,栈为空时操作无定义。


栈的线性表实现
栈可以实现为在一端插入/删除的线性表。在表实现中,执行插入/删除操作的一端被称为栈顶,另一端被称为栈底。访问和弹出的都是栈顶元素。
用线性表实现栈时,操作只在表的一端进行,不涉及另一端,更不涉及表的中间部分。由于这种情况,自然应该选择实现最方便并且保证两个主要操作效率最高的那一端作为栈顶。
1)对于顺序表,尾端插入和删除是O(1)操作,应该用这一端作为栈顶。
2)对于链接表,首端插入和删除是O(1)操作,应该用这一端作为栈顶。
在实际中,栈都采用这两种技术实现。
5.2.2 栈的顺序表实现
实现栈之前,先考虑为操作失败的处理定义一个异常类。由于操作时栈不满足需要(如空栈弹出)可以看作参数值错误,因此自定义异常类可以继承ValueError。
1 class StackUnderflow(ValueError): 2 pass # 不提供ValueError之外的新功能,只是与其他ValueError异常有所区分。必要时可以定义专门的异常处理操作。
采用顺序表技术实现栈,首先会遇到实现顺序表时提出的各类问题,如:是采用简单顺序表,还是动态顺序表?如果采用简单顺序表就可能出现栈满的情况,继续压入元素就会溢出,应该检查和处理。而如果采用动态顺序表,栈的存储区满时可以替换一个更大的存储区,这种情况又会出现存储区的置换策略问题,以及分期付款式的O(1)时间复杂度问题。
list及其操作实际上提供了与栈的使用方式有关的功能,可以直接作为栈来使用。
由于list类型采用的是动态顺序表技术,入栈操作具有分期付款式的O(1)时间复杂度,其他操作都是O(1)时间复杂度。
把list当作栈使用,完全可以满足应用的需要。但是,这样建立的对象还是list,提供了list类型的所有操作,特别是提供了一大批栈结构原本不应该支持的操作,威胁到栈的使用安全性(例如栈要求未经弹出的元素应该存在,但表允许任意删除)。另外,这样的“栈”不是一个独立类型,因此没有独立类型的所有重要性质。
可以自定义一个栈类,把list隐藏在这个类的内部,作为其实现基础。
基于list实现的栈,(沿用list的扩容方式)
1 class SStack(): 2 def __init__(self): 3 self._elems = [] 4 5 def is_empty(self): 6 return self._elems == [] 7 8 def top(self): 9 if self.is_empty(): 10 raise StackUnderflow("in SStack.top()") 11 return self._elems[-1] 12 13 def push(self, elem): 14 self._elems.append(elem) 15 16 def pop(self): 17 # if self._elems == []: 18 if self.is_empty(): 19 raise StackUnderflow("in SStack.top()") 20 return self._elems.pop()
初始创建对象时建立一个空栈;top和pop操作都需要先检查栈的情况,在栈空时引发异常。
属性_elems是只在内部使用的属性,这里采用下划线开头。
1 st1 = SStack() 2 st1.push(3) 3 st1.push(5) 4 while not st1.is_empty(): 5 print(st1.pop())
5.2.3 栈的链表实现
基于顺序表实现的栈可以满足绝大部分的实际需要。考虑基于链表的栈,主要是因为顺序表的两个特点所带来的问题:扩大存储需要做一次高代价操作(替换存储区);顺序表需要完整的大块存储区。采用链表技术,在这两个问题上都有优势,链表的缺点是更多依赖于解释器的存储管理,每个结点的链接开销,以及链接结点在实际计算机内存中任意散布可能带来的操作开销。
由于栈操作都在线性表一端进行,采用链表技术,自然应该把表头一端作为栈顶,表尾作为栈底。
1 class LStack(): 2 def __init__(self): 3 self._top = None 4 5 def is_empty(self): 6 return self._top == None 7 8 def top(self): 9 if self.is_empty(): 10 raise LinkedListUnderflow('in pop') 11 return self._top.elem 12 13 def push(self, elem): 14 # 链表首端添加 15 self._top = LNode(elem, self._top) 16 17 def pop(self): 18 if self.is_empty(): 19 raise LinkedListUnderflow('in pop') 20 e = self._top.elem 21 self._top = self._top.next 22 return e
5.3 栈的应用
基本用途基于两个方面:

顺序反转,只需把所有元素按原来的顺序全部入栈,再顺序出栈,就能得到反序后的序列。整个操作需要O(n)时间。
1 l1 = [1, 3, 5, 7, 9] 2 l2 = [] 3 ls1 = LStack() 4 for i in l1: 5 ls1.push(i) 6 7 while not ls1.is_empty(): 8 l2.append(ls1.pop()) 9 print(l2) # [9, 7, 5, 3, 1]
如果入栈和出栈操作任意交错,可以得到不同的元素序列。
5.3.1 简单应用:括号匹配问题

括号配对原则:在扫描正文过程中,遇到的闭括号应该与此前最近遇到且尚未获得匹配的开括号配对。如果最近的未匹配开括号与当前闭括号不配对,或者找不到这样的开括号,就是匹配失败,说明这段正文里的括号不配对。
由于存在多种不同的括号对,每种括号都可能出现任意多次,而且还可能嵌套。为了检查是否匹配,扫描中必须保存遇到的开括号。由于编程时无法预知要处理的正文里会有多少括号需要保存,因此不能用固定数目的变量保存,必须使用缓存结构。
由于括号的出现可能嵌套,需要逐对匹配:当前闭括号应该与前面最近的尚未配对的开括号匹配,下一个闭括号应该与前面次近的开括号匹配。这说明,需要存储的开括号的使用原则是后进先出的。
进而,如果一个开括号已配对,就应该删除这个括号,为随后的匹配做好准备。
上面这些情况说明,用栈保存遇到的开括号可以正确支持匹配工作。
思路:
1)顺序扫描被检查正文(一个字符串)里的一个个字符。
2)检查中跳过无关字符(非括号字符都是无关字符)。
3)遇到开括号将其入栈。
4)遇到闭括号时弹出栈顶元素与之匹配,如果匹配成功则继续,否则以失败结束。
书中的示例是错的:
1 def check_parens(text): 2 parens = '()[]{}' 3 open_parens = '([{' 4 opposite = {')': '(', ']': '[', '}': '{'} 5 6 ls = LStack() 7 for i in text: 8 if i not in parens: 9 continue 10 if i in open_parens: 11 ls.push(i) 12 continue 13 14 try: 15 s = ls.pop() 16 except: # 当出现一个闭括号,但是没有与之相对的开括号时 17 print('匹配失败') 18 return False 19 if opposite[i] != s: 20 print('匹配失败') 21 return False 22 23 if ls.is_empty(): 24 print('匹配成功') 25 return True 26 else: 27 print('匹配失败') 28 return False 29 30 31 def check_parens2(text): 32 parens = '()[]{}' 33 open_parens = '([{' 34 opposite = {')': '(', ']': '[', '}': '{'} 35 36 def parentheses(text): 37 i, text_len = 0, len(text) 38 while True: 39 while i < text_len and text[i] not in parens: 40 i += 1 41 if i >= text_len: 42 return 43 yield text[i], i 44 i += 1 45 46 ls = LStack() 47 for pr, i in parentheses(text): 48 if pr in open_parens: 49 ls.push(pr) 50 elif ls.pop() != opposite[pr]: 51 print('匹配失败') 52 return False 53 print('匹配成功') 54 return True 55 56 57 text = '((((' 58 check_parens(text) 59 check_parens2(text)
5.3.2 表达式的表示、计算和交换
中缀表示很难统一地贯彻。首先是一元和多元运算符都难以中缀形式表示。其次是不足以表示所有可能的运算顺序,需要通过辅助符号、约定和 /或辅助描述机制。
后缀表达式特别适合计算机处理。
前缀表达式和后缀表达式都不需要引进括号,也不需要任何有关优先级或结合性的规定。对于前缀表示,每个运算符的运算对象,就是它后面出现的几个完整表达式,表达式个数由运算符元数确定。对于后缀表示,情况类似但位置相反。
中缀表达式的表达能力最弱,而给中缀表达式增加了括号后,几种表达式具有同等表达能力。
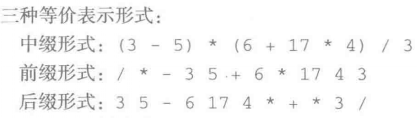

。。。
5.3.3 栈与递归
如果在一个定义中引用了被定义的对象本身,这种定义被称为递归定义。类似地,如果在一种数据结构中的某个或某几个部分具有与整体同样的结构,这也是一种递归结构。

在递归定义或结构中,递归部分必须比原来的整体简单,这样才有可能达到某种终结点(即递归定义的出口),这种终结点必须是非递归的。例如,单链表中,结点链的空链接就是递归的终点。
阶乘函数的递归运算

以fact(6)为例,

这种后进先出的使用方式和数据项数的无明确限制,就说明需要用一个栈来支持递归函数的实际运行,这个栈被称为程序运行栈(算法图解上叫调用栈)。
栈与递归/函数调用
对递归定义的函数,实现方式就是用一个运行栈,对函数的每个调用都在这个栈上为之开辟一块区域,其中保存这个调用的相关信息,这个区域称为一个函数帧。
一般的函数调用和退出的方式也与此类似。例如函数f里调用函数g,函数g里调用函数h,函数h里调用函数r,其执行流程与递归完全一样。
递归和非递归
对递归定义的函数,每个实际调用时执行的都是该函数体的那段代码,只是需要在一个内部运行栈里保存各次调用的局部信息。这种情况说明,完全有可能修改函数定义,把一个递归定义的函数改造为一个非递归的函数。在函数里自己完成上面这些工作,用一个栈保存计算中的临时信息,完成同样的计算工作。
1 def norec_fact(n): 2 res = 1 3 ls = LStack() 4 while n > 0: 5 ls.push(n) 6 n -= 1 7 while not ls.is_empty(): 8 res *= ls.pop() 9 return res
实际上,任何一个递归定义的函数,都可以通过引入一个栈保存中间结果的方式,翻译为一个非递归的过程。
栈的应用:简单背包问题

。。。
5.4 队列
5.4.1 队列抽象数据类型
队列的基本操作也是一个封闭集合,通常包括创建新队列对象、判断队列是否为空、入队、出队、检查队列当前元素。
队列操作与栈操作一一对应,但通常采用另一套习惯的操作名:

5.4.2 队列的链接表实现
采用线性表技术实现队列,就是利用元素位置的顺序表示入队时间的先后关系。队列操作要求先进先出,这就要求在表的两端进行操作,所以实现起来也稍微麻烦一些。
由于需要在链接表的两端操作,在一端插入元素,在另一端删除。最简单的单链表只支持首端高效操作,在另一端操作需要O(n)时间,不适合作为队列的实现基础。
带表尾指针的单链表,支持O(1)时间的尾端插入操作,再加上表首端的高效访问和删除,可作为队列的实现基础。

5.4.3 队列的顺序表实现
基于顺序表实现队列的困难

另一种可能是队首元素出队后表中元素不前移,但记住新队首位置。从操作效率上看,每个操作都是O(1)时间,但表中队列却好像随着操作向表尾方向”移动“,表前端留下越来越多的空位。
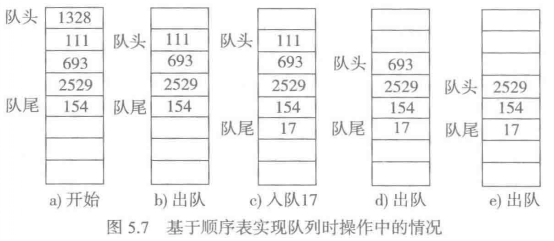
这样经过反复的入队和出队操作,一定会在某次入队时出现队尾溢出的情况,而此时队首却有大量空位,所以这是一种假性溢出,并不是真的用完了整个元素区。假如元素存储区能自动增长,随着操作进行,表首端就会留下越来越大的空区,而且这片空区永远也不会用到。显然不应该允许程序中出现这种情况。
从图5.7可以看到:在反复入队和出队操作中,队尾最终会到达存储区末端。但与此同时,存储区首端可能有些空位可以利用。这样就得到了一种顺理成章的设计:如果入队时队尾已满,应该考虑转到存储区开始的位置去入队新元素。
循环顺序表
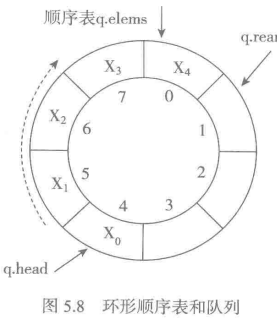
1)在队列使用中,顺序表的开始位置并未改变。变量q.elems始终指向表元素区开始。
2)队头变量q.head记录当前队列里第一个元素的位置;队尾变量q.rear记录当前队列里最后元素之后的第一个空位。
3)队列元素保存在顺序表的一段连续单元里,python的写法是[q.head, q.rear],左闭右开区间。
上面这几条也是这种队列的操作必须维护的性质。初始时队列为空,应该让q.hear和q.rear取相同的值,表示顺序表里一个空段。具体取值无关紧要。不变操作都不改变有关变量的值,不会破坏上述性质;变动操作可能修改有关变量的值,因此要特别注意维护上面的性质。
出队和入队操作分别需要更新变量q.head和q.rear。
1 q.head = (q.head+1) % q.len # 出队 # 通过求余控制循环 2 q.rear = (q.rear+1) % q.len # 入队
判断队列状态。q.head == q.rear表示队空。
从图5.8的队列状态出发做几次入队操作,可以到达图5.9所示的状态,这时队列里已有7个元素。如果再加入一个元素顺序表就满了,但又会出现q.head == q.rear的情况,这个状态与队列空的判断无法区分。
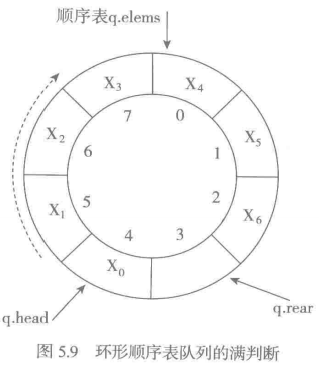
一种解决办法是直接把图5.9“看作”队列已满,即把队满条件定义为
1 (q.rear+1) % q.len == q.head # 队尾撵上队首了
采用这种方法,将在表里留下一个不用的空位。基于循环顺序表,存在多种队列实现方式。
5.4.4 队列的 list 实现
最直截了当的实现方法将得到一个O(1)时间的enqueue操作和O(n)时间的dequeue操作。
现在考虑定义一个可以自动扩充存储的队列类。这里很难直接利用list的自动存储扩充机制,两个原因:首先是队列元素的存储方式与list元素的默认存储方式不一致。list元素总在其存储区的最前面一段,而队列元素可能是其中的任意一段,有时还分为头尾两端(图5.9就是这样,但队列本身仍然是连续的)。如果list自动扩充,其中的队列元素就有可能失控。另一方面,list没提供检查元素存储区容量的机制,队列操作中无法判断系统何时扩容。由于没有很好的办法处理这些困难,下面考虑自己管理存储。
基本设计
首先,队列可能为空而无法dequeue,为此自定义一个异常:
1 class QueueUnderflow(ValueError): 2 pass
基本设计:
1)在SQueue对象里用一个list类型的成分_elems存放队列元素。
2)_head记录队列首元素所在位置的下标。
3)_num记录表中元素个数。
4)_len记录当前表的长度,必要时替换存储区。
数据不变式
变动操作可能会改变一些对象属性的取值,如果操作的实现有错误,可能会破坏对象的状态。实现一种数据结构里的操作时,最基本的问题就是这些操作需要维护对象属性之间的正确关系,这样一套关系被称为这种数据结构的数据不变式。(1)对象的初始状态应该满足数据不变式。(2)每个对象操作都应该保证不破坏数据不变式。有了这两条,这类对象在使用中就能始终处于良好状态。
下面是队列实现中考虑的数据不变式:
1)_elems属性引用着队列的元素存储区,它是一个list对象,_len属性记录存储区的有效容量(python无法获知list对象的实际大小)。
2)_head是队首元素的下标,_num始终记录着队列中元素的个数。
3)队列里的元素总保存在_elems里从_head开始的连续位置中,新入队元素存入_head+_num算出的位置,但如果需要把元素存入下标_len的位置时,改为在下标0位置存入该元素(前提是队列未满,0位置处有空位,否则扩容)。
4)在_num == _len时(队满时)出现入队操作,就扩大存储区。
总之,需要时刻注意_elems、_len、_head、_num四个变量的状态。
队列类的实现
根据前面的设计,队列的首元素在self._elems[self._head],peek和dequeue操作应该取这里的元素;下一个空位在self._elems[(self._head+self._num) % self._len],入队的新元素应该存入这里。
另外,队列空就是self._num == 0,当前队列满就是self._num = self._len,这时应该替换存储区。
完整实例:
1 #!coding:utf8 2 3 class QueueUnderflow(ValueError): 4 pass 5 6 class SQueue(): 7 def __init__(self, init_len=8): 8 self._len = init_len 9 self._elems = [0]*init_len # 感觉用None比较好 10 self._head = 0 11 self._num = 0 12 13 def is_empty(self): 14 return self._num == 0 15 16 def peek(self): 17 if self.is_empty(): 18 raise QueueUnderflow('none') 19 return self._elems[self._head] 20 21 # 时刻注意四个变量的状态 22 # 不能直接使用pop,pop队首的时间为O(n) 23 def dequeue(self): 24 if self.is_empty(): 25 raise QueueUnderflow('none') 26 e = self._elems[self._head] 27 self._head = (self._head + 1) % self._len 28 self._num -= 1 29 return e 30 31 # 不能直接使用append 32 # 可能出现扩容操作 33 def enqueue(self, e): 34 if self._num == self._len: 35 self.__extend() # 扩容 36 37 self._elems[(self._head + self._num) % self._len] = e 38 self._num += 1 39 40 # 扩容(2倍) 41 def __extend(self): 42 old_len = self._len 43 self._len *= 2 44 new_elems = [0]*self._len # 这个一直没有理解?? 45 for i in range(old_len): 46 new_elems[i] = self._elems[(self._head + i) % self._len] 47 self._elems, self._head = new_elems, 0
特别提醒:peek和dequeue操作都需要事先判断队列是否为空。
基于循环顺序表实现的队列,加入和取出操作都是O(1)操作。循环顺序表实际上是为了解决假性溢出问题。
小结:基于链表的队列,链表是指带尾端指针的链表;基于顺序表的队列,顺序表是指循环顺序表。
5.5 迷宫求解和状态空间搜索
5.5.1 迷宫求解:分析和设计

迷宫问题
搜索从入口到出口的路径,具有递归性质:
1)从迷宫的入口开始检查,这是初始的当前位置。
2)如果当前位置就是出口,已经找到出口,问题解决。
3)如果从当前位置已无路可走,当前正在进行的探查失败,需要按一定方式另行继续搜索。
4)从可行方向中取一个,向前进一步,从那里继续探索通往出口的路径。
先考虑一种简单形式的迷宫。如图5.10左图,
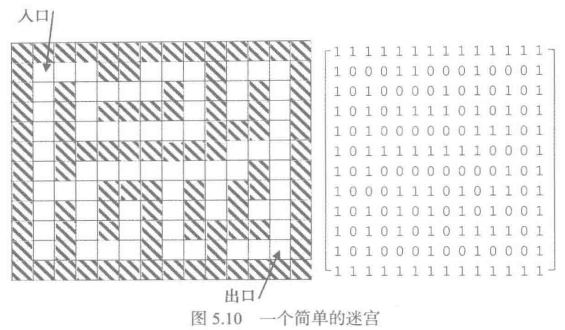
其形式是一组位置构成的矩形阵列,空白格子表示可通行,阴影格子表示不可通行。这种迷宫是平面的,形式比较规范,每个空白位置的上/下/左/右四个方向有可能也是空白位置,每次允许在某个方向上移动一步。这种迷宫可以直接映射到二维的0/1矩阵,因此很容易在计算机里表示。
迷宫问题分析
问题的目标是找到从入口到出口的一条路径,而不是所有的可行路径。
由于不存在其他指导信息,这里的工作方式只能是试探并设法排除无效的探索方向。这显然需要缓存一些信息:如果当前位置有多个可能的继续探查方向,由于下一步只能探查一种可能,因此必须记录不能立即考虑的其他可能方向。不记录而丢掉了重要信息,就可能出现实际有解但不能找到的情况。
存在不同的搜索方式,可以比较冒进,也可以稳扎稳打。如果搜索到当前位置还没找到出口,可以继续向前走,直到无路可走才考虑后退,换一条没走过的路继续。也可以在每一步都从最早记录的有选择位置向前进,找到下一个可达位置并记录它。
显然这里需要保存已经发现但尚未探索的分支方向信息。由于无法确定需要保存的数据项数,只能用某种缓存结构,首先应该考虑使用栈或队列。搜索过程只要求找到目标,对如何找到没有任何约束,因此这两种结构都有可能使用。采用不同的缓存结构,会对所实现的搜索过程有重要影响:
1)按栈的方式保存和使用信息,实现的探索过程是每步选择一种可能方向一直向前,直到无法前进才退回到此前最后选择点,换路径继续该过程。
2)按队列方式保存和使用信息,就是总从最早遇到的搜索点不断拓展。这种方式倒不好理解。。。
问题表示和辅助结构
要解决上述迷宫问题,首先要设计一种问题表示形式。用计算机解决问题,第一步就是选择合适的数据表示。python里可以用二维数组表示。迷宫入口和出口可以各用一对下标表示。
有一个情况需要注意:搜索过程有可能在某些局部路径中兜圈子,这样即使存在到出口的路径,程序也可能无休止地运行却永远也找不到解。为防止出现这种情况,程序运行中必须采用某种方法记录已经探查过的位置,方法是把对应矩阵元素标记为2。计算中发现元素值为2就不再去探索。(0表示可通行,1表示不可通行,2表示已探查)
还需要找到一种确定当前位置可行方向的技术。在到达某个位置后,搜索过程需要选一个方向前进。如果再次退回到这里就需要改走另一方向,直到所有方向都已探查为止,如果还没找到出口就应该退一步。
这里需要记录方向信息。显然,每个格子有四个相邻位置,为正确方便地处理这几个可能方向,需要确定一种系统检查方法。对于单元(i, j),其四个相邻位置的数组元素下标如图所示:(i 表示上下,j 表示左右)
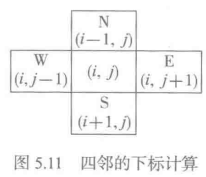
为了方便地计算相邻位置,需要定义一个二元组列表,其元素是从位置(i, j)得到其四邻位置应该加的数对:dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)]
为了使算法的描述更加方便,先定义两个简单的辅助函数。其中参数pos都是形式为(i, j)的二元序对。
1 def mark(maze, pos): # 给迷宫maze的pos位置标2,表示“到过了” 2 maze[pos[0]][pos[1]] = 2 3 4 def passable(maze, pos): # 检查迷宫maze的位置pos是否可行 5 return maze[pos[0]][pos[1]] == 0
5.5.2 求解迷宫的算法
迷宫的递归求解

示例,
1 def mark(maze, pos): # 给迷宫maze的pos位置标2,表示“到过了” 2 maze[pos[0]][pos[1]] = 2 3 4 def passable(maze, pos): # 检查迷宫maze的位置pos是否可行 5 return maze[pos[0]][pos[1]] == 0 6 7 def find_path(maze, pos, end): 8 mark(maze, pos) 9 if pos == end: 10 print(pos, end=' ') 11 return True 12 13 for i in range(4): 14 nextP = (pos[0]+dirs[i][0], pos[1]+dirs[i][1]) 15 if passable(maze, nextP): 16 if find_path(maze, nextP, end): 17 print(pos, end=' ') 18 return True 19 return False 20 21 maze = [ 22 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], 23 [1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1], 24 [1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1], 25 [1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], 26 [1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1], 27 [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1], 28 [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], 29 [1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1], 30 [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1], 31 [1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1], 32 [1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], 33 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] 34 ] 35 pos = (1, 1) 36 end = (10, 12) 37 dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)] 38 print(find_path(maze, pos, end))
栈和回溯法

迷宫的回溯法求解

1 def mark(maze, pos): # 给迷宫maze的pos位置标2,表示“到过了” 2 maze[pos[0]][pos[1]] = 2 3 4 def passable(maze, pos): # 检查迷宫maze的位置pos是否可行 5 return maze[pos[0]][pos[1]] == 0 6
# 自己翻译的, 7 def find_path(maze, start, end): 8 if start == end: 9 print(start) 10 return 11 ls = LStack() 12 ls.push(start) 13 while not ls.is_empty(): 14 pos = ls.pop() 15 for dir in dirs: 16 nextp = pos[0]+dir[0], pos[1]+dir[1] 17 if nextp == end: 18 print(nextp) 19 while not ls.is_empty(): 20 print(ls.pop()) 21 return 22 if passable(maze, nextp): 23 ls.push(pos) 24 ls.push(nextp) 25 break 26 mark(maze, pos) 27
# 书上的,在栈中保存的是(位置序对, 探索方向)序对。 28 def find_path2(maze, start, end): 29 if start == end: 30 print(start) 31 return 32 ls = LStack() 33 mark(maze, start) 34 ls.push((start, 0)) 35 while not ls.is_empty(): 36 pos, nxt = ls.pop() 37 for i in range(nxt, 4): 38 nextp = pos[0]+dirs[i][0], pos[1]+dirs[i][1] 39 if nextp == end: 40 print(nextp) 41 while not ls.is_empty(): 42 print(ls.pop()) 43 return 44 if passable(maze, nextp): 45 ls.push((pos, i+1)) 46 mark(maze, nextp) 47 ls.push((nextp, 0)) 48 break 49 print('not found') 50 51 maze = [ 52 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], 53 [1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1], 54 [1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1], 55 [1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], 56 [1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1], 57 [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1], 58 [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], 59 [1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1], 60 [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1], 61 [1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1], 62 [1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], 63 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] 64 ] 65 pos = (1, 1) 66 end = (10, 12) 67 dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)] 68 find_path(maze, pos, end)
两种方法的区别在于标记的时机不同:方法1是标记当前位置,方法2是标记可达位置。两种方法的关键点相同:一是栈中所存元素相同,一次操作入栈的都是当前位置和可达位置。二是到达出口后打印路径的方式相同(书中没给)。

5.5.3 迷宫问题和搜索

状态空间搜索:栈和队列

基于栈和队列的搜索过程

*深度和宽度优先搜索的性质

5.6.1 几种与栈或队列相关的结构
双端队列

python的deque类

5.6.2 几个问题的讨论
