二叉树

目录

1. 定义
2. 基本概念
3. 二叉树性质
4. 遍历顺序

定义

二叉树是一个连通的无环图，并且每一个顶点的度不大于3,二叉树还要满足根结点的度不大于2。每个顶点定义了唯一的父结点，和最多2个子结点。

基本概念

二叉树是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：

• 空二叉树
• 只有一个根结点的二叉树
• 只有左子树
• 只有右子树
• 完全二叉树

二叉树的性质

1.  在非空二叉树中，第i层的结点总数不超过2^(i-1),i>=1。

2.  深度为h的二叉树最多有2^h-1个结点 h>=1,最少有h个结点。

3. 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1。

4. 具有n个结点的完全二叉树的深度为㏒₂(n+1)

5. 有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：

                                若I为结点编号则 如果I>1，则其父结点的编号为I/2；

                                如果2*I<=N，则其左儿子（即左子树的根结点）的编号为2*I；

                                若2*I>N，则无左儿子；

                                如果2*I+1<=N，则其右儿子的结点编号为2*I+1；

                                若2*I+1>N，则无右儿子。

类型：

完全二叉树：若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化，几乎每次都要考到的二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

满二叉树：除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

平衡二叉树：平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树同时，平衡二叉树必定是二叉搜索树，反之则不一定。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

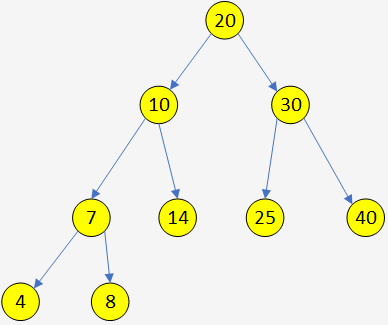
遍历顺序

遍历是对树的基本运算。所谓遍历二叉树，就是按照一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成一个线性序列表示。

设L、D、R分别表示遍历左子树、根节点、右子树。如图

• 先序遍历(DLR)

           首先访问根，再先序遍历左子树，最后先序遍历右子树。 A B E F C H

• 中序遍历(LDR)

           首先中序遍历左子树，再访问根，最后中序遍历右子树。 E B F A H C

• 后序遍历(LRD)

            首先后序遍历左子树，再后续遍历右子树，最后访问根。E F B H C A

层次遍历

即按照层次访问，通常用队列来做。访问根，访问子女，再访问子女的子女（越往后的层次越低）（两个子女的级别相同）

线索二叉树

对于n个结点的二叉树，在二叉链存储结构中有n+1个空链域，利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针，这些指针称为线索，加上线索的二叉树称为线索二叉树。

这种加上了线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同，线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。

如图：中序线索二叉树

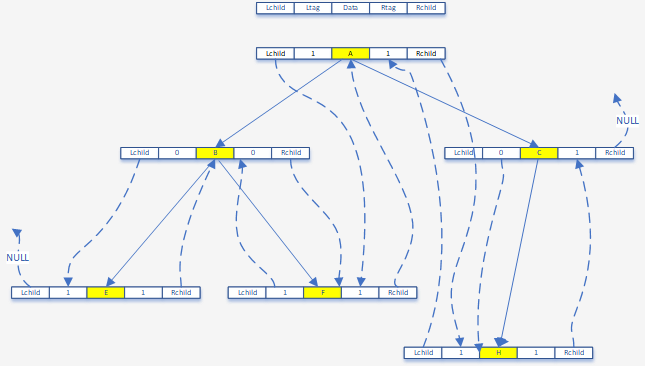
其中：

• ltag=0 时lchild指向左子女；
• ltag=1 时lchild指向前驱；
• rtag=0 时rchild指向右子女；
• rtag=1 时rchild指向后继；

二叉树的遍历本质上是将一个复杂的非线性结构转换成为线性结构，使每个结点都有了唯一的前驱和后继(第一个结点无前驱，最后一个结点无后继)