To the Max(动态规划)

Description

Given a two-dimensional array of positive and negative integers, a sub-rectangle is any contiguous sub-array of size 1*1 or greater located within the whole array. The sum of a rectangle is the sum of all the elements in that rectangle. In this problem the sub-rectangle with the largest sum is referred to as the maximal sub-rectangle. As an example, the maximal sub-rectangle of the array:

0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2 is in the lower left corner:

9 2 -4 1 -1 8 and has a sum of 15.

Input

The input consists of an N * N array of integers. The input begins with a single positive integer N on a line by itself, indicating the size of the square two-dimensional array. This is followed by N^2 integers separated by whitespace (spaces and newlines). These are the N^2 integers of the array, presented in row-major order. That is, all numbers in the first row, left to right, then all numbers in the second row, left to right, etc. N may be as large as 100. The numbers in the array will be in the range [-127,127].

Output

Output the sum of the maximal sub-rectangle.

Sample Input

4
0 -2 -7 0
9 2 -6 2
-4 1 -4  1
-1 8  0 -2

Sample Output

15

题目大意

输入一个N(N最大100)，然后输入N² 个数(每个数的取值范围为：[-127, 127] )，N * N的矩阵，找其中的子矩阵所有元素的和最大的值

解题思路

每行的数等于当前行加上之前行的数，前缀和

$a[i][j] = a[i - 1][j] + 当前数$

假设一开始，数组存储状态如图所示：

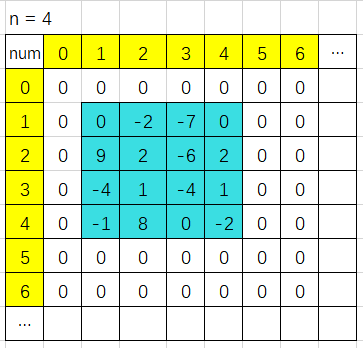
每行数据的每一列 等于 当前列之前行的所有数之和(包括当前行)

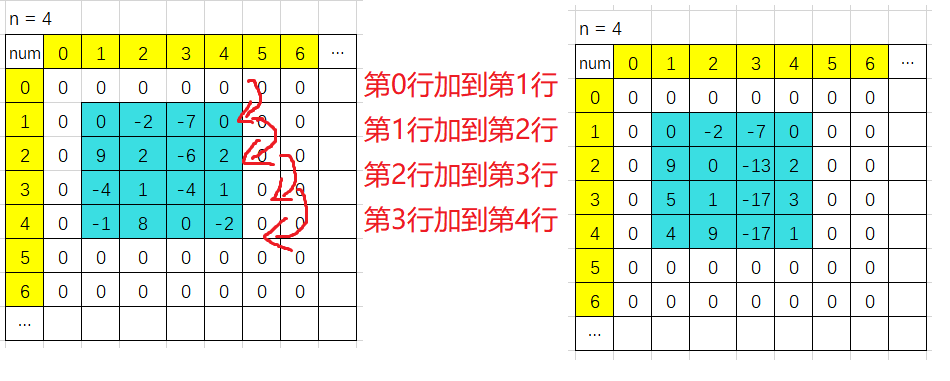
从第x( 1 <= x <= n )行开始

到第y ( x <= y <= n )行结束。遍历找列的最大子段和

num[y][k] - num[x - 1][k]就是第k列的第x行到第y行的所有数之和

其实就是把第x行到第y行每一列的数按列加起来，变成一维数组

然后找其最大子段和

下面是AC代码：

#include <cstdio>
#include <cstdlib>
#include <memory.h>

#define N 105

int num[N][N];

int main()
{
    int n;
    while (~scanf("%d", &n))
    {
        memset(num, 0, sizeof(num));
        int temp;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                scanf("%d", &temp);
                num[i][j] = num[i - 1][j] + temp;
            }
        }

        int max = 0;
        int sum;

        for (int i = 1; i <= n; i++)
        {
            for (int j = i; j <= n; j++)
            {
                sum = 0;
                for (int k = 1; k <= n; k++)
                {
                    temp = num[j][k] - num[i - 1][k];
                    sum = sum > 0 ? sum + temp : temp;
                    max = sum > max ? sum : max;
                }
            }
        }
        printf("%d
", max);
    }
    return 0;
}