二维数组求最大子矩阵的算法 （闫立新 苏海岩）

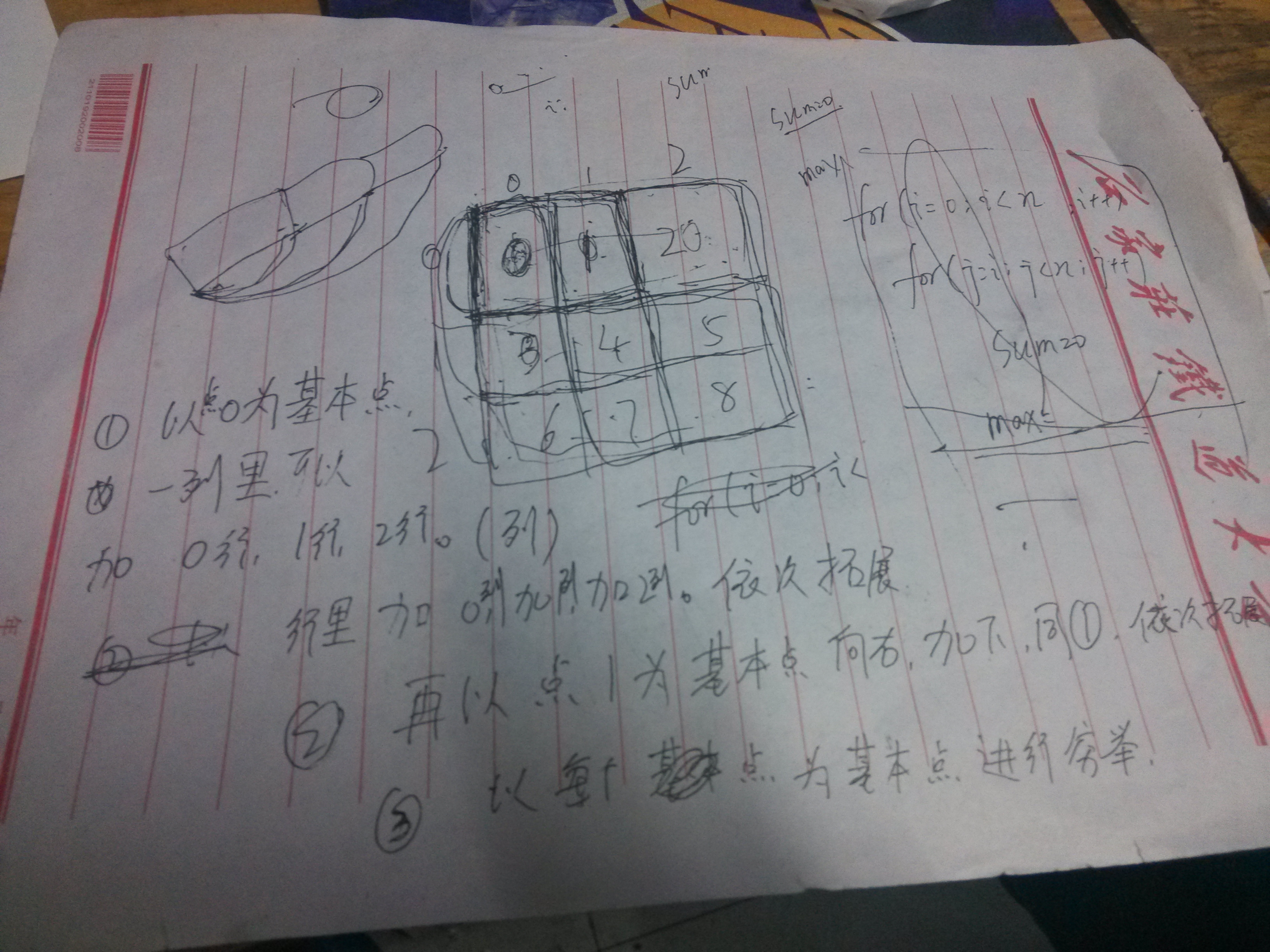
1.一维的情况，设置两个for循环，每一次都加上后面的数。这样通过遍历，把所有可能的数组的和都计算出来。利用max变量保存，只要找到了最大的值就替换，每次都进行更新。在最外层的一次循坏结束后要使sum的值变为0以便不会影响后面一次循环的结果。

int Max(int a[],int n)
{
    int max=-1000;
    int sum;
    for (int i = 0;i < n;i++)
    {
        sum = 0;
        for (int j=i;j<n;j++)
        {
            sum=sum+a[j];
            if (sum>max)
            {
                max=sum;
            }
        }
    }
    return max;
}

2.二维的情况，将矩形压缩，就变成了一维的情况了。也就是说，如果考虑第i行到第j行的矩形，那么只需要知道矩形的每一列从第i行到第j行的和，就可以用一维的算法去求解在该范围内的最大子矩形了。

int maxSubMatrix(int (*ma)[4], int m, int n)
{
int i, j, k, max = ma[0][0], tmp;
int* sum = malloc(m * sizeof(int));
for (i = 0; i < n; i++)
{
for (k = 0; k < m; k++)
sum[k] = 0;
for (j = i; j < n; j++)
{
for (k = 0; k < m; k++)
{
sum[k] += ma[k][j];
}
tmp = maxSubArray(sum, n);
if (tmp > max)
max = tmp;
}
}
free(sum);
return max;
}

在此处用到了一维的函数，找到一行中最大的子数组！

运行结果：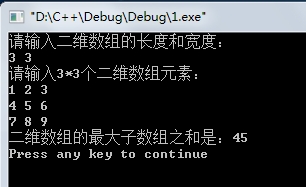

课堂设计思路：