第六章 隐式马尔可夫模型与最大熵模型
马尔可夫模型发展出了隐式马尔可夫模型HMM和最大熵模型MaxEnt,与马尔可夫有关的最大熵模型称为最大熵马尔可夫模型MEMM。
HMM和MEMM都是序列分类器。给定一个单元(单词、字母、语素、句子等)的序列,可以计算在可能的标号上的概率分布,并选择最好的标号序列。
在语音和语言处理中,到处都会遇到序列分类的问题。
MaxEnt并不是序列分类器,因为它常把一个类指派给一个单一的元素。最大熵这个术语来自奥卡姆剃刀发现概率模型的分类器思想。奥卡姆剃刀的思想主张最简单主义(约束最小,熵最大)。
6.1 马尔可夫链
可以把马尔可夫链看做概率图模型。
一阶马尔可夫链中,一个特定状态的概率只与它的前面的一个状态有关。
马尔可夫假设:(P(q_i|q_1...q_{i-1}) = P(q_i|q_{i-1})))
6.2 隐式马尔可夫模型
HMM还有一个假设:一个输出观察(o_i)的概率只与产生该观察的状态(q_i)有关,而与其他的任何观察无关。
输出独立性假设:(P(o_i|q_1...q_i...q_T,o_1....o_i...o_T) = P(o_i|q_i))
在HMM中,任何两个状态之间的转移都有一个非零的概率,称为全连通HMM或遍历HMM。状态之间转移概率为零的,如从左到右的HMM,即Bakis HMM。
三个问题:
似然度问题:给定一个HMM (lambda = (A, B)) 和一个观察序列(O),确定似然度(P(O|lambda))。
解码问题:给定一个HMM (lambda = (A, B)) 和一个观察序列(O),找出最好的隐藏状态序列(Q)。
学习问题:给定一个观察序列(O)和HMM中的状态集合,学习HMM的参数A和B。
6.3 似然度的计算:向前算法
每一个隐藏状态只产生一个单独的观察。所以,隐藏状态序列与观察序列具有相同的长度。
观察序列的似然度为:(P(O|Q) = prod_{i=1}^T P(o_i|q_i))
向前算法是一种动态规划算法,复杂度为(O(N^2T)),当得到观察序列的概率时,它使用一个表来存储中间值。也使用对于生成观察序列的所有可能的隐藏状态的路径上的概率求和的方法来计算观察概率,不过它把每一个路径隐含地叠合在一个单独的向前网络中。
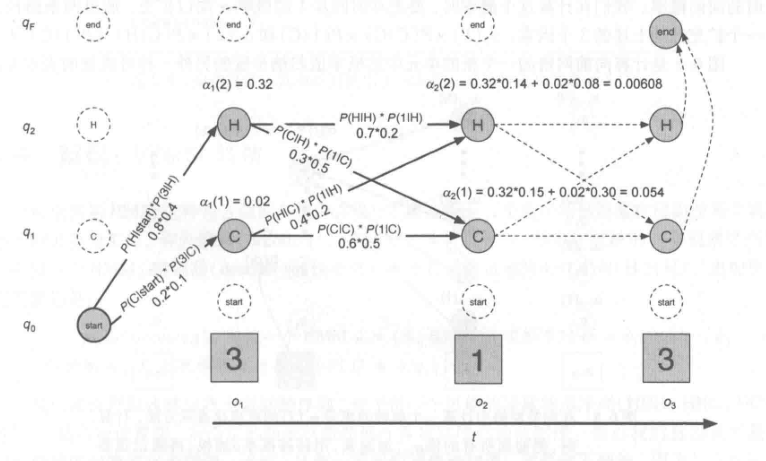

6.4 解码:Viterbi算法
确定哪一个变量序列是隐藏在后面的某个观察序列的来源的工作,称为解码。
Viterbi算法是一个动态规划算法,与最小编辑距离算法类似。
6.5 HMM的训练:向前-向后算法
向前-向后算法,这是期望最大化算法的一个特例。这个算法将帮助我们训练HMM的转移概率A和发射概率B。