监督学习算法--线性，逻辑回归

监督学习算法

线性回归

线性是指回归方程在空间中表现为直线形式,其决策边界是线性的.回归在数学上来说是给定一个点集，能够用一条曲线去拟合之，如果这个曲线是一条直线，那就被称为线性回归

回归中Y变量为连续数值型 分类中Y变量为类别型

一元线性回归又称为简单线性回归模型，是指模型中只有一个自变量和一个因变量，给模型的数学表达式可以表示成： y=ax+b+ξ，类似于一次函数，其中ξ为模型的误差，a和b统称为回归系数。误差项ξ的存在主要是为了平衡等号两边的值，通常被称为模型无法解释的部分ε的方差(variance)对于所有的自变量x是一样的；ε的值是独立的；ε满足正态分布

线性回归“试图学得一个线性模型以尽可能准确地预测实值输出标记。

线性模型试图学得一个通过属性的线性组合来进行预测的函数，即

线性回归模型实际上是基于目标变量与特征变量之间线性相关的假设前提，对研究对象的d个特征变量进行线性组合，从而预测目标变量取值的函数

线性回归模型参数求解的过程，实质上是寻求一条完美直线穿过所有的训练集数据点，使所有数据点到该直线的距离最小，这里的距离通常是指欧式距离

对于线性回归模型，参数估计的常用方法有两种：1.最小二乘法   2.梯度下降法

线性回归模型的损失函数为凸函数,其极小值即为最小值

梯度下降法

顾名思义，梯度下降法就是沿着函数梯度下降的方向寻找极小值。对于线性回归问题，梯度下降法期望通过参数的数次迭代逐渐逼近损失函数的最小值以及参数的最优解，梯度下降法会在每一步走完后，计算对应位置的导数，然后沿着梯度（变化最快的方向）相反的方向前进

作用：最小化一个损失函数

梯度下降法的两种方式

• 批量梯度下降法（BGD）

批量梯度下降法每次迭代都会使用训练集的所有样例数据

批量梯度下降法能够保证每次迭代朝着正确的梯度方向进行，但迭代时间长，计算资源消耗严重

• 随机梯度下降法（SGD）

随机梯度下降法每次迭代只随机使用训练集的一条样例数据

随机梯度下降法虽然迭代次数多，但每次迭代的速度较快。因为每次迭代无法保证正确的梯度方向，损失函数值会出现振荡。

梯度下降法的一个重要超参数是步长（learning rate），用来控制蒙眼人步子的大小，就是下降幅度。 如果步长足够小，那么成本函数每次迭代都会缩小，直到梯度下降法找到了最优参数为止。 但是，步长缩小的过程中，计算的时间就会不断增加。 如果步长太大，这个人可能会重复越过谷底，也就是梯度下降法可能在最优值附近摇摆不定

有时候随机梯度下降法比起批量梯度下降法更不容易陷入局部最优。

• 小批量梯度下降法（MBGD）

小批量梯度下降法综合了ＢGD和SGD的优点，每次迭代使用训练集的多条样例数据。

1. 首先对参数赋值,这个值可以是随机的,也可以让是一个全零的向量.

2. 改变的值,使其损失函数按照梯度下降的方向进行减少,这个方向其实就是减少最快的方向

3. 不断重复2)步骤,使其误差在给定范围内.

这里需要注意：当我们以损失函数进行参数估计时（例如线性回归里面的最小二乘估计），因为是求损失函数最小时的参数（是一个不断下降地逼近最低值），故采用梯度下降法，当我们用最大似然函数进行参数估计时，是求似然函数最大时对应的参数（是一个不断上升地逼近最高值），那么这时时梯度上升法。其实道理都是一样，只是前面正负号的问题

逻辑回归

逻辑回归算法是目前使用最为广泛的一种学习算法，用于解决分类问题。与线性回归算法一样，也是监督学习算法。不用线性回归的原因是，分类问题，y的取值为0或1，如果使用线性回归，那么线性回归模型的输出值可能远大于1，或者远小于0，会导致代价函数很大

为了解决这个问题，我们给出一个激活函数Sigmoid函数：

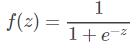
当z=0时，值为0.5 当z不断增大时，值将趋近于1 当z不断减小时，值将趋近于0

Logistic回归算法主要是利用了Sgimoid函数来为数据分类，分类的准确的关键取决于从样本空间中计算出的回归系数，使样本的值向目标值0或1趋近，越接近目标值越好，预测就会越准确

逻辑回归算法的思想是：它的输出值永远在0 到1 之间。

逻辑回归的目的是：将数据二分类，提高准确率

逻辑回归的损失函数是它的极大似然函数

逻辑回归作为一个回归(也就是y值是连续的)，如何应用到分类上去呢。y值确实是一个连续的变量。逻辑回归的做法是划定一个阈值，y值大于这个阈值的是一类，y值小于这个阈值的是另外一类。阈值具体如何调整根据实际情况选择。一般会选择0.5做为阈值来划分

Logistic Regression和Linear Regression的原理是相似的，可以简单的描述为这样的过程：

（1）找一个合适的预测函数，一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。需要对数据有一定的了解或分析，知道或者猜测预测函数的“大概”形式，比如是线性函数还是非线性函数。（2）构造一个Cost函数（损失函数），该函数表示预测的输出（h）与训练数据类别（y）之间的偏差，可以是二者之间的差（h-y）或者是其他的形式。综合考虑所有训练数据的“损失”，将Cost求和或者求平均，记为J(θ)函数，表示所有训练数据预测值与实际类别的偏差。

（3）显然，J(θ)函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法，Logistic Regression实现时有的是梯度下降法（Gradient Descent）。

#####

总结：

线性回归才是真正用于回归的，而不像logistic回归是用于分类，其基本思想是用梯度下降法对最小二乘法形式的误差函数进行优化。单变量线性回归的基本形式就是y = ax + b，用来拟合数据，比如房屋面积和价格的关系。

• 优点：实现简单，计算简单；

• 缺点：不能拟合非线性数据；

Logistic是用来分类的，是一个非线性的二分类模型，主要是计算在某个样本特征下事件发生的概率，但是它本质上又是一个线性回归模型，因为除去sigmoid映射函数，其他的步骤，算法都是线性回归的。可以说，逻辑回归，都是以线性回归为理论支持的。比如根据用户的浏览购买情况作为特征来计算它是否会购买这个商品，抑或是它是否会点击这个商品。然后LR的最终值是根据一个线性和函数再通过一个sigmod function来求得，这个线性和函数权重与特征值的累加以及加上偏置求出来的，所以在训练LR时也就是在训练线性和函数的各个权重值w。

• 优点：实现简单； 分类时计算量非常小，速度很快，存储资源低

• 缺点：容易过拟合，一般准确度不太高； 只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须线性可分；

分类和回归的区别:在于输出变量的类型。

定量输出称为回归，或者说是连续变量预测；定性输出称为分类，或者说是离散变量预测。

举个例子：预测明天的气温是多少度，这是一个回归任务；预测明天是阴、晴还是雨，就是一个分类任务。

总的来说两个问题本质上都是一致的，就是模型的拟合（匹配）。