https://zybuluo.com/ysner/note/1125078
题面
给一个网格,每次把相邻两点连通性改为(1)或(0),询问两点是否联通。
解析
线段树神题。。。
码量巨大,细节巨多。。。
从一座城市走到另一座城市,一共有4种方案。
若两城市在同一行(比如说(s1),(s2)),那么:
s1-->s2
s1-->s3,s3-->s2
s1-->s4,s4-->s2
s1-->s3,s3-->s4,s4-->s2
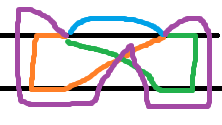
若两城市不在同一行(比如说(s1),(s4)),那么:
s1-->s3,s3-->s4
s1-->s2,s2-->s4
s1-->s3,s3-->s2,s2-->s4
s1-->s4
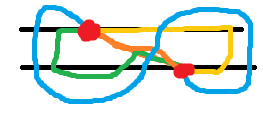
而我们怎么维护这个东西呢?考虑用线段树。每个节点表示区间[l,r]的矩形,并且记录8个变量:(U,D,l,r,u,d,p,q)。其中,(mid=frac{s+t}{2}):
- U:第一行mid,mid+1两列之间是否联通
- D:第二行mid,mid+1两列之间是否联通
- l:s1,s3是否联通
- r:s2,s4是否联通
- u:s1,s2是否联通
- d:s3,s4是否联通
- q:s1,s4是否联通
- p:s3,s2是否联通
发现如果s=t的话,也就是说只有上下2个城市,那么U,D,u,d这4个变量就没有意义了,我们将它们全部赋值为1,避免一些不必要的麻烦。
于是,线段树的操作就变得很显然了。另外注意线段树中的每一个节点只维护这个矩形四个角上的点的连通性,并且我们并不关心它的路径是什么,只考虑使其连通的路径存在于当前矩形的情况。
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#define ll long long
#define re register
#define il inline
#define ls x<<1
#define rs x<<1|1
#define fp(i,a,b) for(re int i=a;i<=b;i++)
#define fq(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
const int N=1e6+100;
struct way{int l,r;}a[N<<2];
struct seg{int U,D,l,r,u,d,p,q;}t[N<<2];
int c,r1,r2,c1,c2;
char s[10];
il int gi()
{
re int x=0,t=1;
re char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
if(ch=='-') t=-1,ch=getchar();
while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
return x*t;
}
il void Merge(seg &x,seg l,seg r)
{
x.l=l.l|(l.u&x.U&r.l&x.D&l.d);
x.r=r.r|(r.u&x.U&l.r&x.D&r.d);
x.u=(l.u&x.U&r.u)|(l.q&x.D&r.p);
x.d=(l.d&x.D&r.d)|(l.p&x.U&r.q);
x.q=(l.u&x.U&r.q)|(l.q&x.D&r.d);
x.p=(l.d&x.D&r.p)|(l.p&x.U&r.u);
}
il void Build(re int x,re int l,re int r)
{
a[x]=(way){l,r};re int mid=l+r>>1;
if(l==r) {t[x].U=t[x].D=t[x].u=t[x].d=1;return;}
Build(ls,l,mid);Build(rs,mid+1,r);
}
il void Updater(re int x,re int p,re int y,re int w)
{
re int l=a[x].l,r=a[x].r;re int mid=l+r>>1;
if(p==mid)
{
if(y==1) t[x].U=w;else t[x].D=w;
Merge(t[x],t[ls],t[rs]);
return;
}
if(p<=mid) Updater(ls,p,y,w);else Updater(rs,p,y,w);
Merge(t[x],t[ls],t[rs]);
}
il void Updatec(re int x,re int p,re int w)
{
re int l=a[x].l,r=a[x].r;re int mid=l+r>>1;
if(l==r) {t[x].l=t[x].r=t[x].p=t[x].q=w;return;}
if(p<=mid) Updatec(ls,p,w);else Updatec(rs,p,w);
Merge(t[x],t[ls],t[rs]);
}
seg Query(re int x,re int ql,re int qr)
{
re int l=a[x].l,r=a[x].r;re int mid=l+r>>1;
if(ql<=l&&r<=qr) return t[x];
if(qr<=mid) return Query(ls,ql,qr);
else if(ql>mid) return Query(rs,ql,qr);
else
{
seg res=t[x];
Merge(res,Query(ls,ql,qr),Query(rs,ql,qr));
return res;
}
}
int main()
{
c=gi();
Build(1,1,c);
while(233)
{
scanf("%s",s);
if(s[0]=='E') break;
r1=gi();c1=gi();r2=gi();c2=gi();
if(c1>c2) swap(c1,c2),swap(r1,r2);
if(s[0]=='O')
if(r1==r2) Updater(1,c1,r1,1);else Updatec(1,c1,1);
if(s[0]=='C')
if(r1==r2) Updater(1,c1,r1,0);else Updatec(1,c1,0);
if(s[0]=='A')
{
seg l=Query(1,1,c1),x=Query(1,c1,c2),r=Query(1,c2,c);
re int ans=0;
if(r1==1&&r2==1)
ans=x.u|(l.r&x.p)|(x.q&r.l)|(l.r&x.d&r.l);
if(r1==1&&r2==2)
ans=x.q|(l.r&x.d)|(x.u&r.l)|(l.r&x.p&r.l);
if(r1==2&&r2==1)
ans=x.p|(l.r&x.u)|(x.d&r.l)|(l.r&x.q&r.l);
if(r1==2&&r2==2)
ans=x.d|(l.r&x.q)|(x.p&r.l)|(l.r&x.u&r.l);
puts(ans?"Y":"N");
}
}
return 0;
}