确定性现象：在一定条件下必然发生的。
统计规律性：在大量重复试验或观察中所呈现出的固有规律性。
随机现象：在个别试验中其结果呈现出不确定性，在大量重复试验中其结果又具有统计规律性的现象。
概率论与数理统计是研究和揭示随机现象统计规律性的一门数学学科。
1、随机试验
随机试验具有三个特点：
可以在相同条件下重复进行；
每次试验的可能结果不止一个，且能在事先明确试验的所有可能结果；
进行一次试验之前不能确定哪一个结果会出现。
2、样本空间、随机事件
把随机试验E的所有可能结果组成的集合称为E的样本空间，记为S，样本空间的元素，即E的每个结果，称为样本点。
样本空间的元素是由试验的目的所确定的。如：投掷三次硬币的正反面结果，和出现正面的次数，这两个随机试验的样本空间不同。
试验E的样本空间的子集，即满足某些条件的子集，称为E的随机事件，简称事件。事件是一个集合。如：灯泡寿命大于500小时的
由一个样本点组成的单点集，称为基本事件。
必然事件
不可能事件
3、频率与概率
频数
频率
当重复试验的次数逐渐增大时，频率f(A)呈现出稳定性，接近于概率P(A)。
概率：设E是随机试验，S是样本空间。对于E的每个事件A赋予一个实数，记为P(A)，称为事件A的概率。满足下列条件：
非负性。P(A)≥0
规范性。P(S)=1
可列可加性。设A1，A2，...是两两不相容的事件，则P(A1UA2U...)=P(A1)+P(A2)+...
4、等可能概型（古典概型）
具有2个特点：
试验的样本空间只包含有限个元素；
试验中每个基本事件发生的可能性相同。
放回抽样
不放回抽样
实际推断原理：人们在长期实践中总结得出“概率很小的事件在一次试验中实际上几乎是不发生的”。
5、条件概率
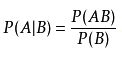为事件A在事件B已发生条件下的发生概率，称为条件概率。满足概率的三个条件。
乘法定理：
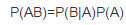
样本空间的划分：S为试验E的样本空间，B1，B2，...Bn为E的一组事件，若
BiBj=0;
B1UB2U...Bn=S
则B1，B2，...Bn为样本空间S的一个划分。
全概率公式：
贝叶斯公式：
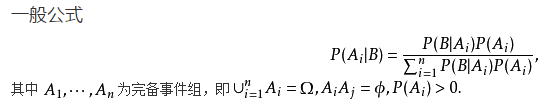
其中，A1，A2，...An是样本空间的一个划分。
6、独立性
设事件A,B是两个事件，如果满足等式P(AB)=P(A)P(B),则称事件A,B相互独立。
定理一：若A,B相互独立，则P(B|A)=P(B)
两个事件相互独立的含义是它们中一个已发生，不影响另一个发生的概率。