树的同构

同构的定义：给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。

更加具体的理解为：两棵树中的每两个对应结点的孩子必须相同，左右位置可不一样。

树的存储结构：结构数组。链表在对输入进行存储时没有数组方便。

如：输入如下样例后结构数组内容

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -

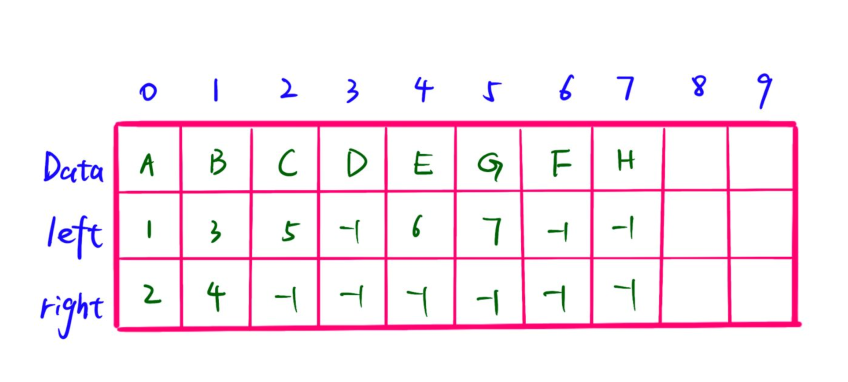
要注意第一个输入的不一定是根结点，没有父亲的结点才是根结点。

定义：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MaxTree 10
#define ElementType char
#define Tree int 
#define Null -1

struct TreeNode {
    ElementType Data;
    Tree left;
    Tree right;
}T1[MaxTree],T2[MaxTree];

Tree Initial(struct TreeNode T1[]);
int Judge(Tree rt1, Tree rt2);

T1,T2为全局数组。

建立二叉树：

Tree Initial(struct TreeNode T[]) {
    int N;
    if(scanf("%d",&N)==1){}
    if (N == 0) {
        return -1;
    }
    int i;
    char c1, c2;
    int flag[MaxTree];
    memset(flag, 0, sizeof(int) * MaxTree);
    getchar();
    for (i = 0;i < N;i ++ ) {
        /*cin >> T[i].Data;
        cin >> c1 >> c2;*/
        if(scanf("%c %c %c",&T[i].Data,&c1,&c2)==3){}
        //T[i].Data=getchar();
        getchar();
        /*c1= getchar();
        getchar();
        c2= getchar();
        getchar();*/
        if (c1 == '-')
            T[i].left = Null;
        else {
            T[i].left = c1 - '0';
            flag[T[i].left] = 1;
        }
        if (c2 == '-')
            T[i].right = Null;
        else {
            T[i].right = c2 - '0';
            flag[T[i].right] = 1;
        }
    }
    for (i = 0;i < N;i++) {
        if (flag[i] == 0)
            break;
    }
    Tree root = i;
    return root;
}

判断是否同构，这里很绕：

int Judge(Tree rt1, Tree rt2) {
    if (rt1 == Null && rt2 == Null)
        return 1;
    if ((rt1 == Null && rt2 != Null) || (rt1 != Null && rt2 == Null))
        return 0;
    if (T1[rt1].Data != T2[rt2].Data)
        return 0;
    if (T1[rt1].left == Null && T2[rt2].left == Null)
        return Judge(T1[rt1].right, T2[rt2].right);
    if (T1[rt1].left != Null && T2[rt2].left != Null && T1[T1[rt1].left].Data == T2[T2[rt2].left].Data)
        return (Judge(T1[rt1].left, T2[rt2].left) && Judge(T1[rt1].right, T2[rt2].right));
    else
        return (Judge(T1[rt1].left, T2[rt2].right) && Judge(T1[rt1].right, T2[rt2].left));
}

前三个if是递归到最简的情况，可以直接判断返回，后面则需要递归。

main：

int main() {
    Tree t1 = Initial(T1);
    Tree t2 = Initial(T2);
    //test(t1);
    if (Judge(t1, t2))
        printf("Yes");
    else
        printf("No");
    return 0;
}