线性回归(Linear Regression)是统计分析、机器学习中最基础也是最重要的算法之一,利用线性函数对一个或多个自变量和因变量(y)之间的关系进行拟合模型,用来做预测。
根据自变量(样本特征)个数分为一元和多元线性回归:
开胃小菜
什么是线性?
首先看看线性函数的定义:一阶或零阶多项式。特征是一维时,线性模型在二维空间构成一条直线;特征是二维时,线性模型在三维空间中构成一个平面;特征是三维时,则最终模型在四维空间中构成一个体;以此类推…
线性回归具体什么时候使用呢?
- 回归问题,因变量是连续值
- 自变量和因变量存在线性关系
其实,这里我们可以大概将线性回归概括为:在N维空间中找到一个线性函数(一条直线,一个平面...)来拟合数据。
看图更直观一些:
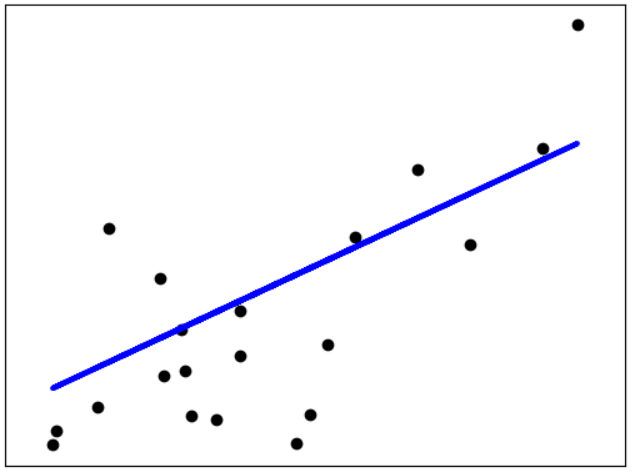
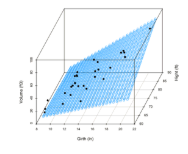
线性回归的目标就是找到图中的直线或平面来拟合图中的点,再结合上述回归方程可以得到:线性回归的目标就是找到回归参数a和b。
怎样找到,且找到最优值呢?
在一个二维空间找到一条直线是简单的,但是怎样找到一条最佳拟合直线是一个值得思索的问题。不妨换一种思路:预测值和真实值之间肯定是存在误差的,那么要是能将误差的最小值找到,就可以使得预测值和真实值无限接近,此时便是最优值。
因此,线性回归可以转换为最小化预测值和真实值误差的问题。
怎样最小化误差呢?
常见有梯度下降法。
实现
机器学习相关的框架和库基本都有实现线性回归的方法,今天介绍用sklearn一个经典实例,预测房价:
from sklearn import datasets
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib as mpl
mpl.use("TkAgg")
import matplotlib.pyplot as plt
boston = datasets.load_boston()
X = boston.data
y = boston.target
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=1/5., random_state=8)
lr = LinearRegression()
lr.fit(x_train, y_train)
y_pred = lr.predict(x_test)
plt.title("linear_regression ")
plt.plot(y_test, color='green', marker='o', label='test')
plt.plot(y_pred, color='red', marker='+', label='predict')
plt.legend()
plt.show()
# 用均方误差评估预测结果
mse = mean_squared_error(y_test, y_pred)
print("MSE:" + repr(mse))
数据集包含了波士顿房屋以及周边环境的一些详细信息,label字段为房屋价格,数据集已经集成到scikit-learn中,可以直接加载数据,通过房屋及其相关的特征使用线性回归预测房屋价格,最后使用均方误差对预测结果进行评估。
总结
线性回归很简单,但是不能拟合非线性数据,并且在实际项目中一般不会单独使用线性回归。
但是,它确是很多强大的非线性模型的基础,蕴含了机器学习中很多重要的思想,还是很值得学习的。
感兴趣的朋友可以对线性回归进行推导。
以上。