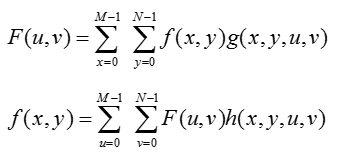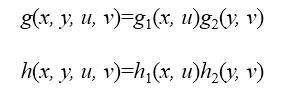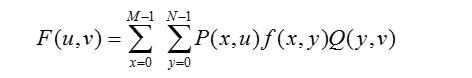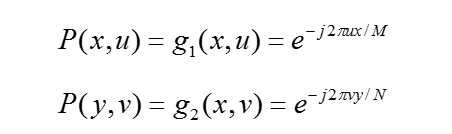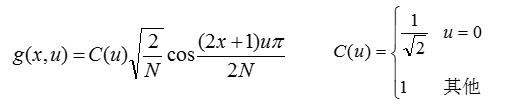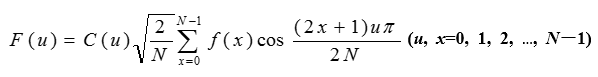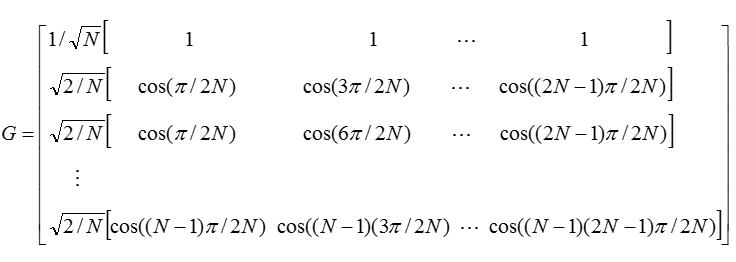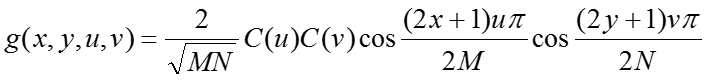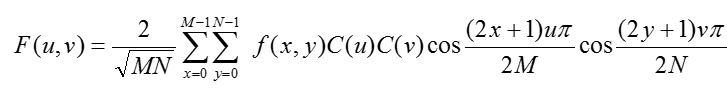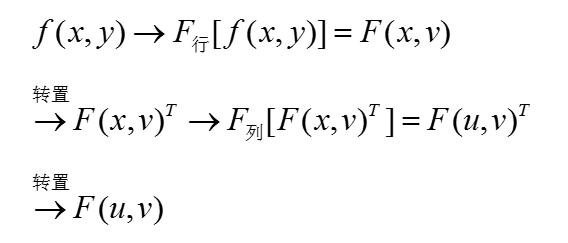1.预备知识
1.1可分离变换
二维傅立叶变换可用通用的关系式来表示:式中:x, u=0, 1, 2, …, M-1;y, v=0, 1, 2, …, N-1;g(x,y,u,v)和h(x,y,u,v)分别称为正向变换核和反向变换核。如果满足 :
则称正、反变换核是可分离的。进一步,如果g1和g2,h1和h2在函数形式上一样,则称该变换核是对称的。2.图像变换的矩阵表示
数字图像都是实数矩阵, 设f(x, y)为M×N的图像灰度矩阵, 通常为了分析、推导方便,可将可分离变换写成矩阵的形式: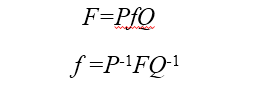 其中,F、f是二维M×N的矩阵;P是M×M矩阵;Q是N×N矩阵。式中,u=0, 1, 2, …, M-1,v=0, 1, 2, …, N-1。对二维离散傅立叶变换,则有 :实践中,除了DFT变换之外,还采用许多其他的可分离的正交变换。例如:离散余弦变换、沃尔什-哈达玛变换、K-L变换等。
其中,F、f是二维M×N的矩阵;P是M×M矩阵;Q是N×N矩阵。式中,u=0, 1, 2, …, M-1,v=0, 1, 2, …, N-1。对二维离散傅立叶变换,则有 :实践中,除了DFT变换之外,还采用许多其他的可分离的正交变换。例如:离散余弦变换、沃尔什-哈达玛变换、K-L变换等。
2.离散余弦变换数学原理
离散余弦变换(Discrete Cosine Transform,DCT)是可分离的变换,其变换核为余弦函数。DCT除了具有一般的正交变换性质外, 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。因此,在对语音信号、图像信号的变换中,DCT变换被认为是一种准最佳变换。2.1一维离散余弦变换定义
一维DCT定义如下: 设{f(x)|x=0, 1, …, N-1}为离散的信号列看看,这里我们就用到了特定核函数的可分离性!将变换式展开整理后, 可以写成矩阵的形式, 即 :F=Gf2.2二维离散余弦变换
二维DCT正变换核为:式中,x, u=0, 1, 2, …, M-1; y, v=0, 1, 2, …, N-1。二维DCT定义如下:设f(x, y)为M×N的数字图像矩阵,则式中: x, u=0, 1, 2, …, M-1; y, v=0, 1, 2, …, N-1。通常根据可分离性, 二维DCT可用两次一维DCT来完成, 其算法流程与DFT类似, 即
3.二维DFT与二维DCT的频谱特征分析
3.1 细节(高频分量)较少的图像实验
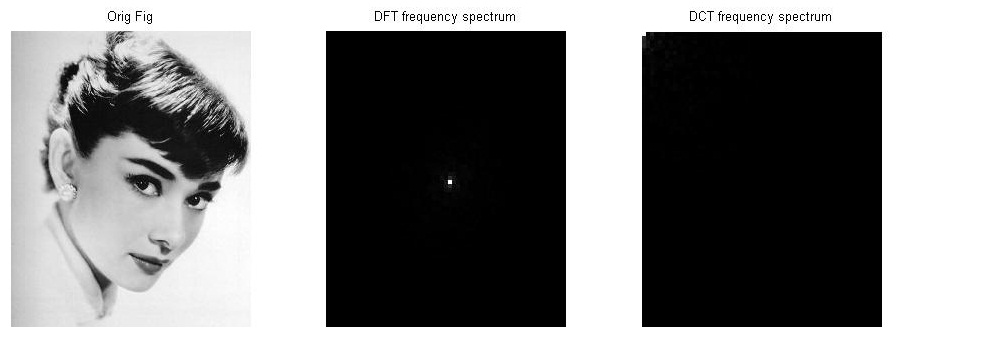
Conclusion:对于比较平滑的图像/数据,DFT变换数据集中在中间(低频信号区),DCT变换数据集中在左上角,几乎无法看出DCT的优势在哪里。3.2 细节丰富的图像实验
Conclusion:DCT变化后的数据很发散,DCT变化后的数据仍然比较集中。如果同样从频率谱恢复原始图像,那么选用DCT更合理,因为DCT只需要存储更少的数据点。正是这个原因,是的DCT广泛地应用于图像压缩。
4.DCT应用于图像压缩
16*16 进行分区做DCT变换,然后按照不同的模板进行数据存留与重建。我们会发现,如果保存的数据过少,会有块效应现象发生。64*64的分区设置,块效应更明显。此时就要在每个分区内多采集点数据啦。
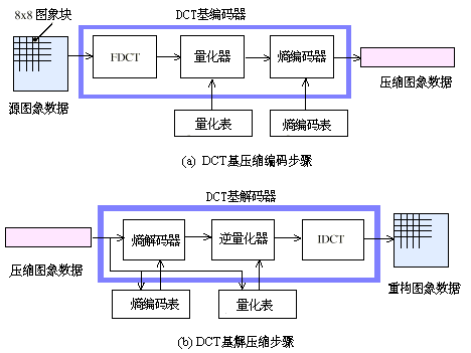
6.简介DCT在JPEG压缩编码中的应用
JPEG(Joint Photographic Experts Group) 专家组开发了两种基本的压缩算法,一种是采用以离散余弦变换(DCT)为基础的有损压缩算法,另一种是采用以预测技术为基础的无损压缩算法。使用有损压缩算法时,在压缩比为25:1的情况下,压缩后还原得到的图像与原始图像相比较,非图像专家难于找出它们之间的区别,因此得到了广泛的应用。JPEG算法的主要计算步骤
- 正向离散余弦变换(FDCT)
- 量化(quantization)
- Z字形编码(zigzag scan)
- 使用差分脉冲编码调制(differential pulse code modulation,DPCM)对直流系数(DC)进行编码
- 使用行程长度编码(run-length encoding,RLE)对交流系数(AC)进行编码
- 熵编码(entropy coding
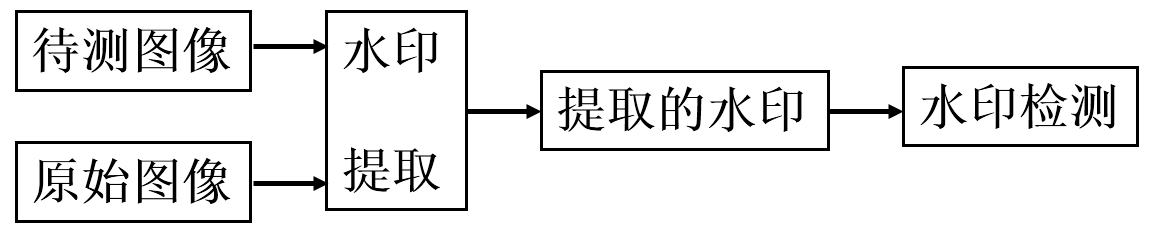
数字水印技术是将特定的信息嵌入到数字信息的内容中,要求嵌入的信息不能被轻易的去除,在一定的条件下可以被提取出来,以确认作者的版权。水印嵌入框图:水印检测框图: