模拟退火 学习笔记

马上要WC了，学个骗分算法玩玩。。

一开始不懂的时候觉得挺神奇，挺万能，现在学会了又不指望能派上用场了/wn

一言以蔽之，曰：“玄”。

爬山算法

先讲爬山。给定一个函数，我们要求出它的全局最优值（最大/最小）。爬山算法采用以下策略：

1. 随便选择一个解。选择一个初始温度(T_0)（一般取很大，(10)的几次方这种）、终止温度(T_e)（(>0)但是很接近(0)，一般取(10)的负几次方）、降温系数(Delta T)（(<1)但是很接近(1)），一开始温度(T=T_0)；
2. 根据当前解生成出一个附近的解（如果是一般意义上的函数，则这个新解与原解距离最好与当前温度有关，如果做不到有关就算了）；
3. 如果新解更优，则用新解替换当前解；
4. 降温，即令(T=TcdotDelta T)。若(Tgeq T_e)则回到第(2)步不断重复，否则退出循环；
5. 返回当前解对应的函数值。

不难发现，其中“根据当前解生成出一个附近的解”这一步要求两个方案的优劣程度与两个方案的相似程度有关，换句话说，我们有可能从一个较优解推出另一个较优解。否则这一步就没有任何道理可言。

对于生成新解这个操作，如果函数的自变量是个比较常规的整数或实数，或者多维也没关系，这样可以给每一维加上一个随机数乘以(T)；而如果自变量是一个方案，是一个排列或组合方式，那么一般方法是交换其中两个元素，这个不太做得到与(T)相关。

很多blog里都说复杂度是(mathrm O( ext{玄学}))，其实根本就不是……不难发现降温次数是(mathrm O!left(-log_{Delta T}dfrac{T_0}{T_e} ight))，再乘上一次算新解并计算函数值的时间复杂度，不就得出总时间复杂度了吗……不难发现，(T_0,T_e)的大小并不很有所谓，平方一下复杂度只乘了个(2)，常数而已，所以一般开的很大/很小。而(Delta T)就很有所谓了，在末尾加一个(9)可能复杂度就增加了一个数量级。

这种爬山算法有一个很大的劣势：在单峰或者峰少并且几个峰靠的比较近的情况下海星，然鹅这种情况下通常有更简单的方法，不需要用玄学；而对于其他的一般情况下的函数，它很容易陷入局部最优解，如下图：

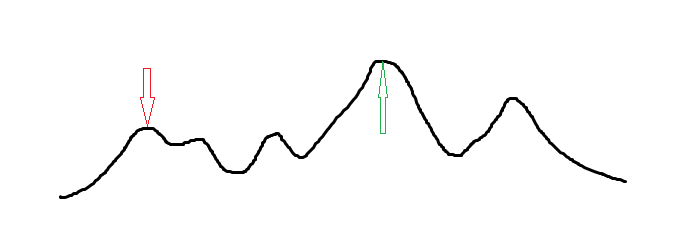
上图中，全局最优解是绿箭头，而爬山算法很容易陷入红箭头无法自拔。于是需要引入模拟退火算法。这样爬山算法就被抛弃在一旁了，一般都不用它而用模拟退火，这也是为什么本篇学习笔记的标题不包含爬山

模拟退火

模拟退火基于爬山算法，引入了一个新的概念：当步骤(3)中，如果新解更劣，那么也有一定概率用新解替换当前解，这一定程度上解决了爬山算法中陷入局部最优解的问题，因为它有可能跳出来。

设原解和新解的函数值分别为(x,x')，那么替换的概率是：

[mathrm e^{frac{-|x-x'|}{T}} ]

这个大概是仿照金属退火设计的算法，按照物理学里的现象，大概可以证明，若模拟退火算法从无穷高的温度开始，以无限趋于(1)的降温系数，经过一定时间降到无限趋于(0mathrm K)的温度，得出的解一定是最优解（概率为(1)）。可惜计算机效率有限，只能退一定次数的火，虽然效果很好，但是并不能保证找到的是最优解。

放一张wikipedia里的图：

优化

这里讲的优化当然是正确性的优化啦………………

本人经验尚浅，只练过五题，简单总结一下吧。

首先，调参要从娃娃抓起。这里影响正确性的参数有：(T_0)、(T_e)、(Delta T)、算新解方式、随机数种子。其中前两个讲过了；(Delta T)一般来说越大，一次模拟退火的正确率越高；算新解方式可以根据具体情况选择；随机数种子是纯玄学，可以随便换然后看脸。

考虑跑多次模拟退火取最优。可以卡时，即while(clock()<CLOCKS_PER_SEC*_____/*略小于TL*/)ans=max/min(ans,sim_ann());。这种情况下考虑尽量优化一次算函数值的时间，这样让模拟退火跑的次数尽量多。

考虑随便选几个种子交几波，然后看情况，若时间允许，将几个种子结合在一个程序里（都跑一遍），这样AC的点的集合是这几个种子单独跑的AC的点的集合的并集。

还可以考虑分段模拟退火，即将函数图像分成几个区间分别跑然后合并，这样可以减少一次模拟退火范围内峰的个数，更容易获得最优解。

例题

（按水过的顺序）

洛谷 P4035 - 球形空间产生器

洛谷题目页面传送门

给定(n)维空间的(n+1)个坐标，它们在同一个(n)维球面上，你需要确定球心坐标。精确到小数点后(6)位。

(nin[1,10])，所有值的绝对值不超过(2 imes10^4)。

这是%你退火最经典的题了。正解似乎是高斯消元，然鹅我不会。于是拿%你退火水。

不难想到，是否是球心是一个关于坐标的函数。但如果直接这样，那么这个函数值是个(0/1)，实在是太无法参考了。于是，这个点到所有给定点的距离相等，可以转化为这些距离的方差等于(0)，这也达到了方差的下限。于是查找这个方差函数的最小值即可。

顺便科普一下，(n)维坐标系下的欧拉距离是(sqrt{sumlimits_{i=0}^{n-1}(x_{1,i}-x_{2,i})^2})。很好证，从二维一维一维推即可。

然后就退火了。初始解选，每一维的坐标是该维下所有给定点的坐标的算术平均。(T_0=10^7,T_e=10^{-9},Delta T=0.97)，每次算新解是(forall iin[0,i),x'_i=x_i+(R(0,100)-R(0,100))T)（其中(R(l,r))表示区间([l,r])内的随机实数），然后卡时，交上去70pts。改成(Delta T=0.9997)，90pts。改成(Delta T=0.9999)，AC（意识到了，“调参要从娃娃抓起”这句话不是说给分块、根号分治听的）。然后算了一下，一遍模拟退火是退约(3 imes10^5)次火，而每次又要(mathrm O!left(n^2 ight))计算方差，这样根本就跑不了几次模拟退火。于是把卡时去掉，只跑一次，照样AC……结合下面的题，可以得出一个经验：对于这种维数少、一脸函数样子的，尽可能提高(Delta T)并只跑一遍模拟退火效果比较好，而对于那种排列方式啊啥的、那种脑子正常的人都不会把方案当成函数的自变量的那种，减小(Delta T)并跑很多次甚至卡时可能会效果比较好（这里(T_0,T_e)没太大讨论价值，调到很大、很小即可，它并不会对效率产生多少影响）。

代码（要开O2，不然只跑一遍模拟退火也会T）：

#include<bits/stdc++.h>
using namespace std;
#define urd uniform_real_distribution
#define mp make_pair
#define X first
#define Y second
const double inf=1e18;
mt19937 rng(998244353);
const int N=10;
int n;
double x[N+2][N];
double dis[N+2];
double calc(vector<double> v){
	double avg=0,res=0;
	for(int i=1;i<=n+1;i++){
		dis[i]=0;
		for(int j=0;j<n;j++)dis[i]+=(x[i][j]-v[j])*(x[i][j]-v[j]);
		avg+=dis[i];
	}
	avg/=n+1;
	for(int i=1;i<=n+1;i++)res+=(avg-dis[i])*(avg-dis[i]);
	return res;
}
vector<double> sim_ann(double st,double ed,double delta){//模拟退火 
	pair<double,vector<double> > res(0,vector<double>(n));
	for(int i=0;i<n;i++){
		for(int j=1;j<=n+1;j++)res.Y[i]+=x[j][i];
		res.Y[i]/=n+1;
	}
	res.X=calc(res.Y);
	for(double tem=st;tem>=ed;tem*=delta){ 
		vector<double> v=res.Y;
		for(int i=0;i<n;i++)v[i]+=(urd<>(0,100)(rng)-urd<>(0,100)(rng))*tem;//算新解 
		double nw=calc(v);
		if(nw<res.X||urd<>(0,1)(rng)<=exp((res.X-nw)/tem))res=mp(nw,v);
	}
//	cout<<res.X<<"
";
	return res.Y;
}
int main(){
	cin>>n;
	for(int i=1;i<=n+1;i++)for(int j=0;j<n;j++)cin>>x[i][j];
	vector<double> ans=sim_ann(1e7,1e-9,.9999);
	for(int i=0;i<ans.size();i++)printf("%.3lf ",ans[i]);
	return 0;
}

洛谷 P3878 - 分金币

分jb

洛谷题目页面传送门

题意见洛谷。

这个也直接模拟退火，把分组情况当作自变量。每次算新解是随机交换两组中的各一个金币（这个就不太好跟当前温度联系上了）。(T_0=10^6,T_e=10^{-6},Delta T=0.97)，由于这个是多测，不方便卡时，于是每组测试点跑(100)次。AC。如果把(Delta T)提到(0.9999)并且只跑一次，WA成一片，0pts……

有个要注意的地方，就是两部分可能有一部分大小为(0)，由于是用vector存的，它的size()-1会爆unsigned int。。。要特判一下。

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define uid uniform_int_distribution
#define urd uniform_real_distribution
#define pb push_back
const int inf=0x3f3f3f3f3f3f3f3f;
mt19937 rng(20060617);
const int N=30;
int n;
int a[N+1];
int sim_ann(double st,double ed,double delta){//模拟退火 
	int sum1=0,sum2=0;
	vector<int> v1,v2;
	for(int i=1;i<=n/2;i++)v1.pb(a[i]),sum1+=a[i];
	for(int i=n/2+1;i<=n;i++)v2.pb(a[i]),sum2+=a[i];
	for(double tem=st;tem>=ed;tem*=delta){
		int x=uid<>(0,v1.size()-1)(rng),y=uid<>(0,v2.size()-1)(rng);//算新解 
		int sum1_0=sum1-v1[x]+v2[y],sum2_0=sum2-v2[y]+v1[x];
		if(abs(sum1_0-sum2_0)<abs(sum1-sum2)||urd<>(0,1)(rng)<=exp((abs(sum1-sum2)-abs(sum1_0-sum2_0))/tem))
			swap(v1[x],v2[y]),sum1=sum1_0,sum2=sum2_0;
	}
	return abs(sum1-sum2);
}
void mian(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	if(n==1)return cout<<a[1]<<"
",void();//特判
	int tim=100,ans=inf;
	while(tim--)ans=min(ans,sim_ann(1e6,1e-6,.97));
	cout<<ans<<"
";
}
signed main(){
	int testnum;
	cin>>testnum;
	while(testnum--)mian();
	return 0;
}

洛谷 P2538 - 城堡

吉利的题号

有人还不信模拟退火可以切黑题？

洛谷题目页面传送门

题意见洛谷。

把自己选的城堡的集合当作自变量即可模拟退火。

考虑先用Floyd预处理出任意两个点间的最短路，然后每次算函数值都是(mathrm O!left(n^2 ight))。考虑用set维护修改，做到(mathrm O(nlog n))？那样(mathrm O(log))乘上STL常数（你值得拥有）还不一定有(mathrm O(n))块力，弃了。

跟上一题一样的套路，参数都一样的，卡时。一开始卡了(0.7mathrm s)（(mathrm{TL}=0.8mathrm s)），96pts，然后随机种子(20060617 o19260817)，卡到(0.75mathrm s)就AC了。例题2 P3878和这题（例题3）都是属于这种方案是一个全集的子集的，这个按照当前经验是适合开小(Delta T)并跑多次模拟退火的。因为你想，如果把方案按bitmask的方式表示出来，这样并不满足相邻的相似度高，有的改一个高位可能相距很远，有的改好多位可能距离为(1)，并看不出什么“峰”，一次并不容易找到最大值，玄学性蛮强的（就是说这并不满足正常的函数的性质，很不连续）。都玄得比较顺利，因为不太用调参/cy

吃了上一题的亏，这次记得特判了/cy

代码：

#include<bits/stdc++.h>
using namespace std;
#define pb push_back
#define uid uniform_int_distribution
#define urd uniform_real_distribution
const int inf=0x3f3f3f3f;
mt19937 rng(19260817);
const int N=50;
int n,m,s;
int to[N+1];
int dis[N+1][N+1];
int cas[N+1];
bool iscas[N+1];
int calc(){
	int res=-inf;
	for(int i=1;i<=n;i++){
		int mn=inf;
		for(int j=1;j<=n;j++)if(iscas[j])mn=min(mn,dis[i][j]);
		res=max(res,mn);
	}
	return res;
}
int sim_ann(double st,double ed,double delta){//模拟退火 
	vector<int> yes,no;
	memset(iscas,0,sizeof(iscas));
	for(int i=1;i<=m;i++)iscas[cas[i]]=true;
	for(int i=1,j=1;i<=min(s,n-m);j++)if(!iscas[j])iscas[j]=true,yes.pb(j),i++;
	for(int i=1;i<=n;i++)if(!iscas[i])no.pb(i);
	int res=calc();
	if(yes.empty()||no.empty())return res;//特判 
	for(double tem=st;tem>=ed;tem*=delta){
		int x=uid<>(0,yes.size()-1)(rng),y=uid<>(0,no.size()-1)(rng);//算新解 
		iscas[yes[x]]=false;iscas[no[y]]=true;
		int nw=calc();
		if(nw<res||urd<>(0,1)(rng)<=exp((res-nw)/tem))res=nw,swap(yes[x],no[y]);
		else iscas[yes[x]]=true,iscas[no[y]]=false;
	}
	return res;
}
int main(){
	cin>>n>>m>>s;
	for(int i=1;i<=n;i++)cin>>to[i],to[i]++;
	memset(dis,0x3f,sizeof(dis));
	for(int i=1;i<=n;i++)dis[i][i]=0;
	for(int i=1;i<=n;i++){
		int x;
		cin>>x;
		dis[i][to[i]]=dis[to[i]][i]=min(dis[i][to[i]],x);
	}
	for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)
		dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
	for(int i=1;i<=m;i++)cin>>cas[i],cas[i]++;
	int ans=inf;
	while(clock()<CLOCKS_PER_SEC*.75)ans=min(ans,sim_ann(1e6,1e-6,.97));
	cout<<ans;
	return 0;
}

洛谷 P3936 - Coloring

我又来水黑题了

话说这个好像不算是水的？似乎没有啥正经做法？

洛谷题目页面传送门

题意见洛谷。

把染色情况当作自变量，然后模拟退火。每次算新解依然随机交换。

注意到，这里一个方案是比较大的，(mathrm O(n^2))，我们可以把(Delta T)开大点（哈哈哈真香了吧，这跟例题2、3是一样的，其实这里根本没啥道理可言），然后再卡时（(mathrm{TL}=5mathrm s)呢）。(T_0=10^6,T_e=10^{-6},Delta T=0.99999)，卡(3mathrm s)不然容易T。不难想到更新新解的函数值是可以做到(mathrm O(1))。

代码：

#include<bits/stdc++.h>
using namespace std;
#define pb push_back
#define mp make_pair
#define X first
#define Y second
#define uid uniform_int_distribution
#define urd uniform_real_distribution
const int inf=0x3f3f3f3f;
mt19937 rng(20060617);
bool chkmn(int &x,int y){return y<x?x=y,true:false;}
const int N=20,M=N,S=50;
int n,m,s;
int a[S+1];
int ans0[N+1][M+1];
int now[N+2][M+2];
vector<pair<int,int> > pos[S+1];
int sim_ann(double st,double ed,double delta){//模拟退火 
	int now0=1,now1=0;
	for(int i=1;i<=s;i++)pos[i].clear();
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){
		now[i][j]=now0,now1++;
		pos[now0].pb(mp(i,j));
		if(now1==a[now0])now0++,now1=0;
	}
	int res=0;
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)res+=(i<n&&now[i][j]!=now[i+1][j])+(j<m&&now[i][j]!=now[i][j+1]);
	for(double tem=st;tem>=ed;tem*=delta){
		int x=uid<>(1,s)(rng),y=uid<>(1,s)(rng); 
		int xx=uid<>(0,pos[x].size()-1)(rng),yy=uid<>(0,pos[y].size()-1)(rng);//算新解 
		int nw=res;
		nw-=(x!=now[pos[x][xx].X-1][pos[x][xx].Y])+(x!=now[pos[x][xx].X+1][pos[x][xx].Y])+(x!=now[pos[x][xx].X][pos[x][xx].Y-1])+(x!=now[pos[x][xx].X][pos[x][xx].Y+1]);
		nw-=(y!=now[pos[y][yy].X-1][pos[y][yy].Y])+(y!=now[pos[y][yy].X+1][pos[y][yy].Y])+(y!=now[pos[y][yy].X][pos[y][yy].Y-1])+(y!=now[pos[y][yy].X][pos[y][yy].Y+1]);
		swap(now[pos[x][xx].X][pos[x][xx].Y],now[pos[y][yy].X][pos[y][yy].Y]);
		nw+=(y!=now[pos[x][xx].X-1][pos[x][xx].Y])+(y!=now[pos[x][xx].X+1][pos[x][xx].Y])+(y!=now[pos[x][xx].X][pos[x][xx].Y-1])+(y!=now[pos[x][xx].X][pos[x][xx].Y+1]);
		nw+=(x!=now[pos[y][yy].X-1][pos[y][yy].Y])+(x!=now[pos[y][yy].X+1][pos[y][yy].Y])+(x!=now[pos[y][yy].X][pos[y][yy].Y-1])+(x!=now[pos[y][yy].X][pos[y][yy].Y+1]);
		if(nw<res||urd<>(0,1)(rng)<=exp((res-nw)/tem))res=nw,swap(pos[x][xx],pos[y][yy]);
		else swap(now[pos[x][xx].X][pos[x][xx].Y],now[pos[y][yy].X][pos[y][yy].Y]);
//		cout<<tem<<" "<<res<<"
";
	}
	return res;
}
int main(){
	cin>>n>>m>>s;
	for(int i=1;i<=s;i++)cin>>a[i];
	int ans=inf;
	while(clock()<CLOCKS_PER_SEC*3)if(chkmn(ans,sim_ann(1e6,1e-6,.99999))){
		for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)ans0[i][j]=now[i][j];
	}
	for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)cout<<ans0[i][j]<<" ";puts("");}
	return 0;
}

AtCoder abc157_f - Yakiniku Optimization Problem

好的，这是我的最后一道模拟退火练习题，来AtC上撒个野。真心不想再玄了。

洛谷题目页面传送门 & AtC题目页面传送门

给定平面上(n)个点((x_i,y_i))，你需要选一个点((x,y))，这样到时间(c_isqrt{(x_i-x)^2+(y_i-y)^2})以后点(i)就可以吃了。你需要最小化至少能吃到(m)个点的时间。一个测试点AC当且仅当绝对误差或相对误差不超过(10^{-6})。

(nin[1,60],|x_i|,|y_i|in[-1000,1000],c_iin[1,100])。

这题正解是二分还是啥的？不会。不难发现至少能吃到(m)个点的时间是一个关于你选的点的坐标的函数，仅有二维，比较良心，一脸可以模拟退火的样子。

然后就写了。注意这里如何计算函数值，把(n)个时间算出来再排个序，取第(m)个即可。在本地调一调，最终(T_0=10^4,T_e=10^{-10},Delta T=0.9999)，算新解的时候采用(x'=x+left(Rleft(0,10^4 ight)-Rleft(0,10^4 ight) ight)T,y'=y+left(Rleft(0,10^4 ight)-Rleft(0,10^4 ight) ight)T)，只跑一遍模拟退火（因为这个维数仅有两维，按照经验提高(Delta T)是要比跑多次效果好的），这样可以过样例，精度还可以。

然后交，随机种子选20060617->1******7->998244353->114514交了四发，到第四发的时候发现第二发和第四发过的点的集合的并等于全集。又注意到每次交大概是(250mathrm{ms})，那么可以把这两发综合起来，用两个种子各跑一遍，AC。

代码：

#include<bits/stdc++.h>
using namespace std;
#define urd uniform_real_distribution
mt19937 rng(19260817);
double sq(double x){return x*x;}
const int N=60;
int n,m;
double x[N+1],y[N+1],c[N+1];
double a[N+1];
double calc(double x0,double y0){
	for(int i=1;i<=n;i++)a[i]=c[i]*sqrt(sq(x[i]-x0)+sq(y[i]-y0));
	sort(a+1,a+n+1);
	return a[m];
}
double sim_ann(double st,double ed,double delta){//模拟退火 
	double x0=0,y0=0,res=calc(0,0);
//	int cnt=0;
	for(double tem=st;tem>=ed;tem*=delta){
		double nw_x=x0+(urd<>(0,10000)(rng)-urd<>(0,10000)(rng))*tem;
		double nw_y=y0+(urd<>(0,10000)(rng)-urd<>(0,10000)(rng))*tem;//生成新解 
		double nw=calc(nw_x,nw_y);
		if(nw<res||urd<>(0,1)(rng)<=exp((res-nw)/tem))x0=nw_x,y0=nw_y,res=nw;
//		if((++cnt)%100==0)printf("tem=%.5lf x=%.5lf y=%.5lf res=%.5lf
",tem,x0,y0,res);
	}
	return res;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>x[i]>>y[i]>>c[i];
	double ans=sim_ann(1e4,1e-10,.9999);
	rng=mt19937(114514);//换种子 
	ans=min(ans,sim_ann(1e4,1e-10,.9999));
	printf("%.10lf",ans);
	return 0;
}

Last but not least

个人不太喜欢这个算法，也不想深入研究下去玄学中的规律与道理……正确的OI精神应该是尽力想正解，而不是用骗分算法水。正如dy鸽鸽所说：不能用乱搞（动手）的勤快，来掩盖思维的懒惰。