排序算法对比，步骤，改进，java代码实现

前言

发现是时候总结一番算法，基本类型的增删改查的性能对比，集合的串并性能的特性，死记太傻了，所以还是写在代码里，NO BB,SHOW ME THE CODE!

github地址：https://github.com/247292980/sort。欢迎各位优化我写的算法代码，还有别看了就完了，fork到自己的仓库里面，或者加入这个项目一起写，拿来怼面试还是很好的。

图片镇楼

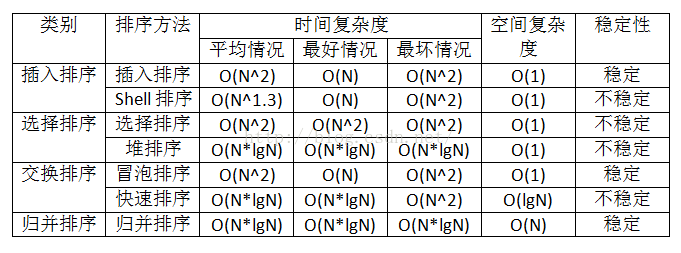
插入排序（InsertSort）

步骤：

      1.依次选择一个待排序的记录，

      2.依次与已经排好序的有序序列比较，并插入

      3.持续每次对越来越少的元素重复上面的步骤，直到插完所有元素为。

改进：

　　二分插入排序，直接和有序序列的中间比较。

　　希尔排序。

 代码：

   /**
     * 直接插入排序的方法
     **/
    private static void directInsertSort(int[] array) {
        //输出原数组的内容
//        printArr(array);
        for (int i = 1; i < array.length; i++) {
            for (int j = 0; j < i; j++) {
                if (array[i] < array[j]) {
                    int temp = array[i];
                    array[i] = array[j];
                    array[j] = temp;
                }
            }
            //输出排序后的相关结果
//            printArr(array);
        }
    }

/**
 * 二分排序
 */
public static void binarySort(int[] source) {
    //printArr(source);
    for (int i = 1; i < source.length; i++) {
        // 查找区上界
        int low = 0;
        // 查找区下界
        int high = i - 1;
        //将当前待插入记录保存在临时变量中
        int temp = source[i];
        while (low <= high) {
            // 找出中间值 右移比除法块
            int mid = (low + high) >> 1;
            //如果待插入记录比中间记录小
            if (temp < source[mid]) {
                // 插入点在低半区
                high = mid - 1;
            } else {
                // 插入点在高半区
                low = mid + 1;
            }
        }
        //将前面所有大于当前待插入记录的记录后移
        for (int j = i - 1; j >= low; j--) {
            source[j + 1] = source[j];
        }

        //将待插入记录回填到正确位置
        source[low] = temp;
        //printArr(source);
    }
}

希尔排序（又叫缩小增量排序，ShellSort）

步骤：

       1.先将整个待排元素序列分割成若干个子序列

       2.分别进行插入排序

　　 3.然后依次缩减增量再进行插入排序

       4.待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次插入排序

 代码：

   /**
     * 希尔排序
     */
    public static void shellSort(int[] arrays) {
//        printArr(arrays);//增量
        int incrementNum = arrays.length / 2;
        while (incrementNum >= 1) {
            for (int i = 1; i < arrays.length; i++) {
                //进行插入排序
                for (int j = 0; j < arrays.length - incrementNum; j = j + incrementNum) {
                    if (arrays[j] > arrays[j + incrementNum]) {
                        int temple = arrays[j];
                        arrays[j] = arrays[j + incrementNum];
                        arrays[j + incrementNum] = temple;
                    }
                }
            }
            //设置新的增量
            incrementNum = incrementNum / 2;
//            printArr(arrays);
        }
    }

冒泡排序（BubbleSort）

步骤：

      1.比较相邻的元素。如果第一个比第二个大，就交换他们两个。

      2.对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

      3.针对所有的元素重复以上的步骤，除了最后一个。

      4.持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

改进：

　　快速排序。

 代码：

    /**
     * 冒泡排序
     */
    public static void bubbleSort(int[] arr) {
//        printArr(arr);
        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = 0; j < arr.length - i - 1; j++) {
                if (arr[j + 1] < arr[j]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
//            printArr(arr);
        }
    }

快速排序（QuickSort）

步骤：

       1.从数列中挑出一个元素，称为 "基准"，重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。

       2.递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。

       3.递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。

 代码：

 /**
     * 快速排序
     */
    public static void quickSort(int[] a, int low, int high) {
        int start = low;
        int end = high;
        int key = a[low];
        printArr(a);

        while (end > start) {
            //从后往前比较
            //如果没有比关键值小的，比较下一个，直到有比关键值小的交换位置，然后又从前往后比较
            while (end > start && a[end] >= key) {
                end--;
            }
            if (a[end] <= key) {
                int temp = a[end];
                a[end] = a[start];
                a[start] = temp;
            }
            //从前往后比较
            //如果没有比关键值大的，比较下一个，直到有比关键值大的交换位置
            while (end > start && a[start] <= key) {
                start++;
            }
            if (a[start] >= key) {
                int temp = a[start];
                a[start] = a[end];
                a[end] = temp;
            }
            //此时第一次循环比较结束，关键值的位置已经确定了。左边的值都比关键值小，右边的值都比关键值大，但是两边的顺序还有可能是不一样的，进行下面的递归调用
        }
        //递归
        if (start > low) {
            quickSort(a, low, start - 1);//左边序列。第一个索引位置到关键值索引-1
        }
        if (end < high) {
            quickSort(a, end + 1, high);//右边序列。从关键值索引+1到最后一个
        }
    }

选择排序(SelectSort)

步骤：

      1.在未排序序列中找到最小（大）元素，存放到排序序列的起始位置

      2.从剩余未排序元素中继续寻找最小（大）元素

      3.放到已排序序列的末尾

      4.以此类推，直到所有元素均排序完毕。

改进：

       传统的简单选择排序,每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素(当前趟最大和最小记录)的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序,最多只需进行[n/2]趟循环即可。

　　堆排序。

 代码：

 /**
     * 选择排序
     */
    public static void selectionSort(int[] a) {
        printArr(a);
        int n = a.length;
        for (int i = 0; i < n; i++) {
            int k = i;
            // 找出最小值的小标
            for (int j = i + 1; j < n; j++) {
                if (a[j] < a[k]) {
                    k = j;
                }
            }
            // 将最小值放到排序序列末尾
            if (k > i) {
                int tmp = a[i];
                a[i] = a[k];
                a[k] = tmp;
            }
            printArr(a);

        }
    }

堆排序（HeapSort）

步骤：

      1.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

      2.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

      3.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序

 代码：

 /**
     * 堆排序
     */
    public static void heapSort(int[] array) {
        //printArr(array);
        array = buildMaxHeap(array);
        //printArr(array);
        System.out.println();
        for (int i = array.length - 1; i > 1; i--) {
            //将堆顶元素和堆低元素交换，即得到当前最大元素正确的排序位置
            int temp = array[0];
            array[0] = array[i];
            array[i] = temp;
            //整理，将剩余的元素整理成堆
            adjustDownToUp(array, 0, i);
            //printArr(array);
        }
    }

    /**
     * 插入操作:向大根堆array中插入数据data
     */
    public int[] insertData(int[] array, int data) {
        //将新节点放在堆的末端
        array[array.length - 1] = data;
        int k = array.length - 1;
        int parent = (k - 1) / 2;
        while (parent >= 0 && data > array[parent]) {
            array[k] = array[parent];
            k = parent;
            //继续向上比较
            if (parent != 0) {
                parent = (parent - 1) / 2;
            } else {
                break;
            }
        }
        array[k] = data;
        return array;
    }

    /**
     * 删除堆顶元素操作
     */
    public int[] deleteMax(int[] array) {
        //将堆的最后一个元素与堆顶元素交换，堆底元素值设为-99999
        array[0] = array[array.length - 1];
        array[array.length - 1] = -99999;
        //对此时的根节点进行向下调整
        adjustDownToUp(array, 0, array.length);
        return array;
    }

    /**
     * 构建大根堆：将array看成完全二叉树的顺序存储结构
     */
    private static int[] buildMaxHeap(int[] array) {
        //从最后一个节点array.length-1的父节点（array.length-1-1）/2开始，直到根节点0，反复调整堆
        for (int i = (array.length - 2) / 2; i >= 0; i--) {
            adjustDownToUp(array, i, array.length);
        }
        return array;
    }

    /**
     * 调整树形结构
     */
    private static void adjustDownToUp(int[] array, int k, int length) {
        int temp = array[k];
        //i为初始化为节点k的左孩子，沿节点较大的子节点向下调整
        for (int i = 2 * k + 1; i < length - 1; i = 2 * i + 1) {
            //取节点较大的子节点的下标
            if (i < length && array[i] < array[i + 1]) {
                //如果节点的右孩子>左孩子，则取右孩子节点的下标
                i++;
            }
            //根节点 >=左右子女中关键字较大者，调整结束
            if (temp >= array[i]) {
                break;
            } else {
                //将左右子结点中较大值array[i]调整到双亲节点上，修改k值，以便继续向下调整
                array[k] = array[i];
                k = i;
            }
        }
        //被调整的结点的值放人最终位置
        array[k] = temp;
    }

归并排序（MergeSort）

步骤：

        1. 把长度为n的输入序列分成两个长度为n/2的子序列。

        2. 对这两个子序列分别采用归并排序。

        3. 将两个排序好的子序列递归合并成一个最终的排序序列。

 代码：

/**
     * 归并排序
     */
    private static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2;
            //左边归并排序，使得左子序列有序
            mergeSort(arr, left, mid, temp);
            //右边归并排序，使得右子序列有序
            mergeSort(arr, mid + 1, right, temp);
            //将两个有序子数组合并操作
            merge(arr, left, mid, right, temp);
        }
    }

    /**
     * 归并
     */
    private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left;
        int j = mid + 1;
        //临时数组指针
        int t = 0;
        while (i <= mid && j <= right) {
            if (arr[i] <= arr[j]) {
                temp[t++] = arr[i++];
            } else {
                temp[t++] = arr[j++];
            }
        }
        while (i <= mid) {//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while (j <= right) {//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while (left <= right) {
            arr[left++] = temp[t++];
        }
        //printArr(arr);
    }

桶排序(Bucket Sort)

步骤：

        1. 创建等容量的桶数组，并将桶数组元素都初始化为0

        2. 逐个遍历数组，将数组的值，作为桶数组的下标。数据被读取时，就将桶的值加1。

        3. 将桶数组不为0的的值的key取出，数量为该key的值

改进：

       基数排序。计数排序

 代码：

 /**
     * 桶排序
     */
    public static void bucketSort(int[] nums, int maxNum) {
        int[] sorted = new int[maxNum + 1];
        for (int i = 0; i < nums.length; i++) {
            sorted[nums[i]] += 1;
        }
        int[] temp = new int[nums.length];
        for (int i = 0, j = 0; i < sorted.length; i++) {
            while (sorted[i] != 0) {
                temp[j++] = i;
                sorted[i] -= 1;
//                printArr(temp);
            }
        }
    }

基数排序(Radix Sort)

步骤：

        1. 将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。

        2. 从最低位开始，依次进行一次排序。

 代码：

   /**
     * 基数排序
     */
    public static void radixSort(int[] arr, int max2) {
        // exp 指数。当对数组按各位进行排序时，exp=1；按十位进行排序时，exp=10；...
        // 从个位开始，对数组a按"指数"进行排序
//        printArr(arr);

        for (int exp = 1; max2 / exp > 0; exp *= 10) {
            // 存储"被排序数据"的临时数组
            int[] output = new int[arr.length];
            int[] buckets = new int[10];

            // 将数据出现的次数存储在buckets[]中
            for (int a : arr) {
                buckets[(a / exp) % 10]++;
            }
//            printArr(buckets);

            // 更改buckets[i]。目的是让更改后的buckets[i]的值，是该数据在output[]中的位置。
            for (int i = 1; i < 10; i++) {
                buckets[i] += buckets[i - 1];
            }
//            printArr(buckets);

            // 将数据存储到临时数组output[]中
            for (int i = arr.length - 1; i >= 0; i--) {
                output[buckets[(arr[i] / exp) % 10] - 1] = arr[i];
//                System.out.println(i);
//                System.out.println((arr[i]));
//                System.out.println((arr[i] / exp));
//                System.out.println((arr[i] / exp) % 10);
//                System.out.println(buckets[(arr[i] / exp) % 10]);
//                System.out.println(buckets[(arr[i] / exp) % 10] - 1);
//                printArr(output);
                buckets[(arr[i] / exp) % 10]--;
            }
//            printArr(buckets);

            // 将排序好的数据赋值给a[]
            System.arraycopy(output, 0, arr, 0, arr.length);
//            printArr(arr);
        }
    }

计数排序（count sort）

步骤：

1. 找出序列中最大值和最小值，开辟Max-Min+1的辅助空间
2. 最小的数对应下标为0的位置，遇到一个数就给对应下标处的值+1,。
3. 遍历一遍辅助空间，就可以得到有序的一组序列
    

代码：

    /**
     * 计数排序
     */
    private static void countSort(int[] array, int max) {
//        printArr(array);

        // 存储"被排序数据"的临时数组
        int[] temp = new int[array.length];
        int[] buckets = new int[max + 1];
        for (int i = 0; i < array.length; i++) {
            buckets[array[i]] += 1;
        }
        // 更改buckets[i]。目的是让更改后的buckets[i]的值，是该数据在output[]中的位置。
        for (int i = 1; i < max + 1; i++) {
            buckets[i] += buckets[i - 1];
        }
        for (int i = array.length - 1; i >= 0; i--) {
            temp[buckets[array[i]] - 1] = array[i];
            buckets[array[i]]--;
//            printArr(temp);
        }
    }