> ############################################线性回归 > setwd("/Users/yaozhilin/Downloads/R_edu/data") > creditcard_exp<-read.csv("creditcard_exp.csv") > head(creditcard_exp,3) id Acc avg_exp avg_exp_ln gender Age Income Ownrent Selfempl dist_home_val 1 19 1 1217.03 7.104169 1 40 16.03515 1 1 99.93 2 5 1 1251.50 7.132098 1 32 15.84750 1 0 49.88 3 95 0 NA NA 1 36 8.40000 0 0 88.61 dist_avg_income age2 high_avg edu_class 1 15.93279 1600 0.10236053 3 2 15.79632 1024 0.05118421 2 3 7.49000 1296 0.91000000 1 > attach(creditcard_exp) > lm<-lm(avg_exp~Income) > summary(lm) Call: lm(formula = avg_exp ~ Income) Residuals: Min 1Q Median 3Q Max -608.11 -215.85 -82.69 202.90 772.50 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 258.05 104.29 2.474 0.0158 * Income 97.73 12.99 7.524 1.6e-10 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 332.1 on 68 degrees of freedom (30 observations deleted due to missingness) Multiple R-squared: 0.4543, Adjusted R-squared: 0.4463 F-statistic: 56.61 on 1 and 68 DF, p-value: 1.603e-10
多元线型回归
#####多元线性回归 > #探究平均支出与年龄和收入等的线型关系 > lm_m<-lm(avg_exp~Age+Income+dist_avg_income+dist_home_val) > coef(lm_m) (Intercept) Age Income dist_avg_income dist_home_val -32.007774 1.372317 -166.720391 261.882708 1.532862
线型回归模型中的截距intercept一般忽略,现实中很少有数据都为零的实例,看income与avg_exp为负相关,我们仔细想想是不合逻辑的,后面肯定得调整。
> summary(lm_m) Call: lm(formula = avg_exp ~ Age + Income + dist_avg_income + dist_home_val) Residuals: Min 1Q Median 3Q Max -504.07 -208.81 -40.92 129.69 681.02 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -32.008 186.874 -0.171 0.86454 Age 1.372 5.605 0.245 0.80735 Income -166.720 87.607 -1.903 0.06147 . dist_avg_income 261.883 87.807 2.982 0.00402 ** dist_home_val 1.533 1.057 1.450 0.15177 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 311.3 on 65 degrees of freedom (30 observations deleted due to missingness) Multiple R-squared: 0.5416, Adjusted R-squared: 0.5134 F-statistic: 19.2 on 4 and 65 DF, p-value: 1.823e-10
看看自变量的显著值,age为0.807,dist_home_val为0.15都不显著,而且R2为0.54,调整R2为0.51,相差还是挺大的,所以后续考虑删除和合并一些变量
自变量的筛选
变量筛选有向前逐步法、向后逐步法、向前向后逐步法。衡量某一变量是否筛选在R中看指标AIC,AIC越小,模型越稳健。
> ###用向前向后逐步法筛选自变量 > #direction = c("both", "backward", "forward") > lm_ms<-step(lm_m,direction = "both") Start: AIC=808.53 avg_exp ~ Age + Income + dist_avg_income + dist_home_val Df Sum of Sq RSS AIC - Age 1 5810 6306104 806.60 <none> 6300294 808.53 - dist_home_val 1 203889 6504183 808.76 - Income 1 351031 6651325 810.33 - dist_avg_income 1 862197 7162491 815.51 Step: AIC=806.6 avg_exp ~ Income + dist_avg_income + dist_home_val Df Sum of Sq RSS AIC <none> 6306104 806.60 - dist_home_val 1 205826 6511930 806.85 - Income 1 345396 6651501 808.33 + Age 1 5810 6300294 808.53 - dist_avg_income 1 857139 7163244 813.52
我们用到step函数,direction=“both”表示向前向后逐步法,我们看看程序是怎么运行筛选变量的。
Start: AIC=808.53,第一步放入所有的变量AIC=808.53
然后我们尝试去掉每一个变量看看AIC的值,发现去掉年龄时AIC最小为806.6,所以我们把Age去掉
第三步我们再次去掉其他的值看看AIC是否下降,并且尝试加上Age看看AIC的值,发现都不如去掉Age时AIC的值小
线型回归模型的诊断
模型已经进行了初步的变量筛选,但远远没有达到建模要求,我们需要对模型进行诊断。
我线性回归理论中提到,最小二乘求得的线性回归模型是有六大假设条件的:
- Y的平均值能够准确地被由X组成的线性函数建模出来。
- 解释变量之间不存在线性关系(或强相关)。
- 解释变量和随机扰动项不存在线性关系。
- 假设随机扰动项是一个均值为0的正态分布。
- 假设随机扰动项的方差恒为定
- 假设随机扰动项是独立的。
我们现在主要检测残差是否符合假设
#####线性回归的诊断 ###残差检验 cre<-na.omit(creditcard_exp) lm<-lm(avg_exp~Income) summary(lm) cre$pred<-predict(lm) cre$res<-resid(lm) plot(cre$res~cre$pred)#呈现喇叭口形状,说明异方差,可以用lny尝试
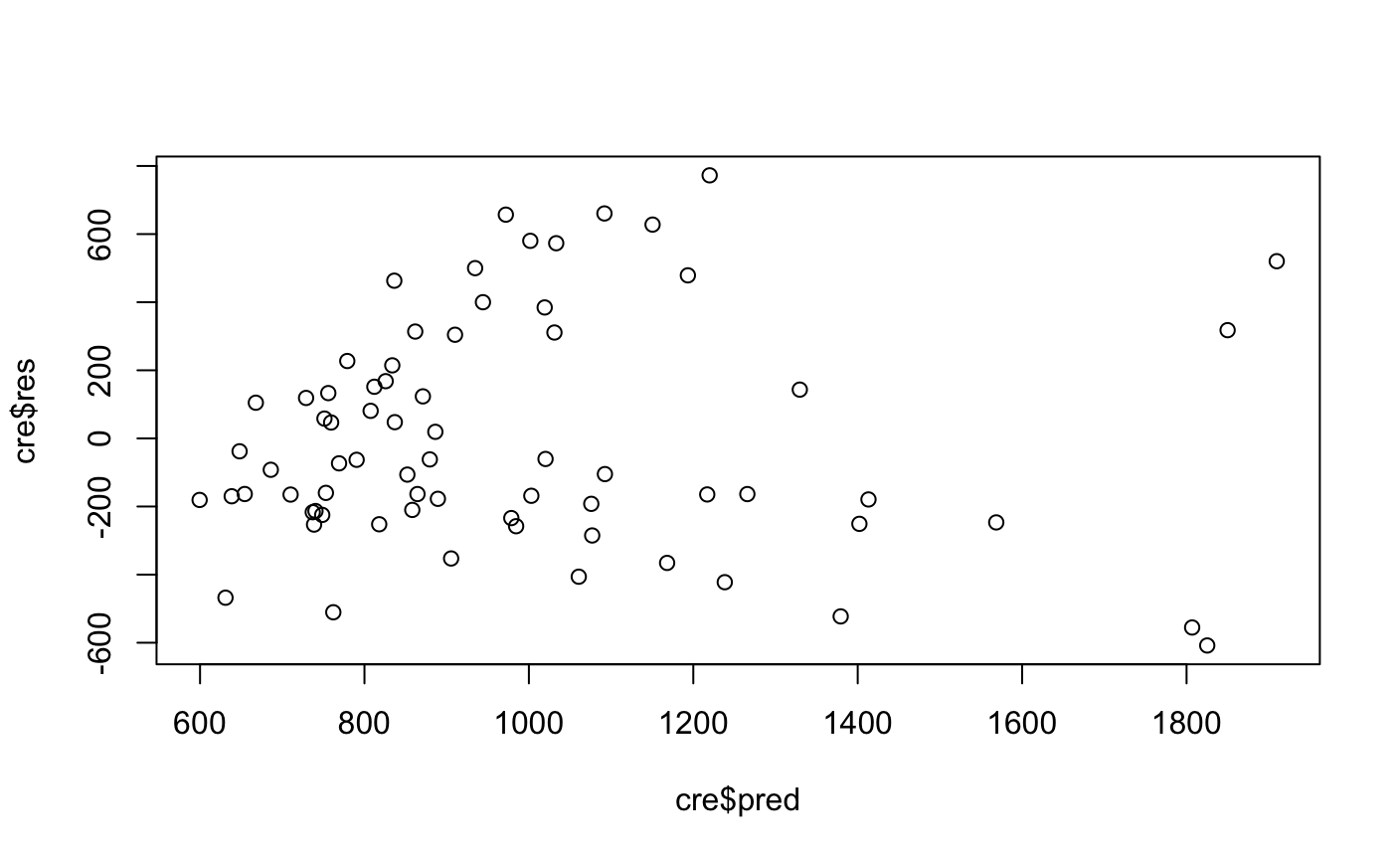
> library(lmtest) > bptest(lm)#检验残差是否显著 studentized Breusch-Pagan test data: lm BP = 12.467, df = 1, p-value = 0.0004142
看得出结果是显著的
> #用lny调整残差存在异方差的模型 > lm1<-lm(avg_exp_ln~Income) > summary(lm1) Call: lm(formula = avg_exp_ln ~ Income) Residuals: Min 1Q Median 3Q Max -1.33858 -0.21063 -0.03193 0.24935 0.61969 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 6.05875 0.11634 52.077 < 2e-16 *** Income 0.09819 0.01449 6.776 3.58e-09 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.3705 on 68 degrees of freedom (30 observations deleted due to missingness) Multiple R-squared: 0.4031, Adjusted R-squared: 0.3943 F-statistic: 45.92 on 1 and 68 DF, p-value: 3.578e-09 > cre$pred1<-predict(lm1) > cre$res1<-resid(lm1) > library(lmtest) > bptest(lm1) studentized Breusch-Pagan test data: lm1 BP = 0.60895, df = 1, p-value = 0.4352 > plot(cre$res1~cre$pred1)
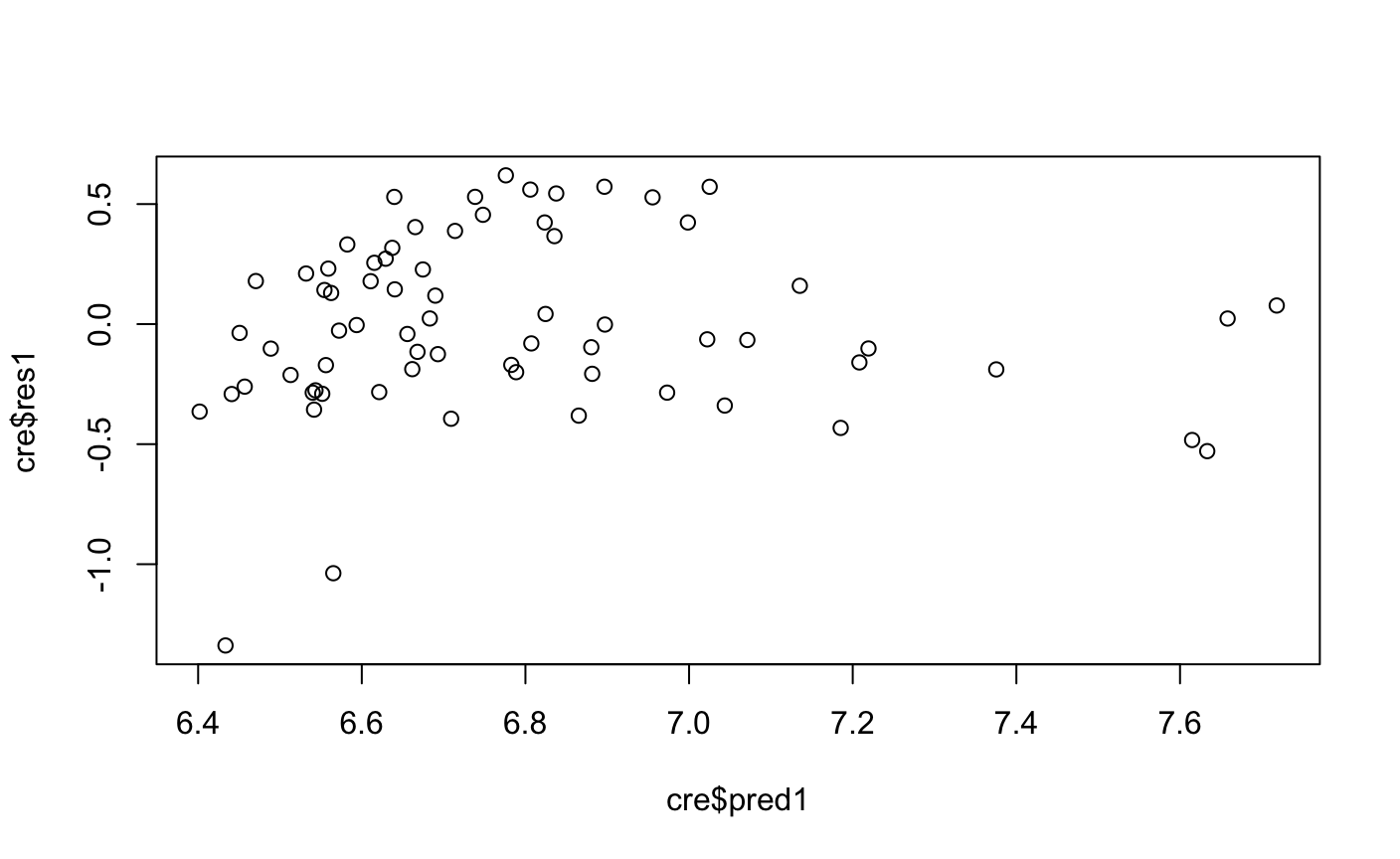
lny~x表示x每变化一个单位,y变化一个百分点,但从模型来看R2变为了0.40,比之前y~x的模型下降了,说明这模型解释是无理的。我们接下来继续探索。
> #用logy、logx调整残差存在异方差的模型 > cre$Income_log<-log(cre$Income) > lm2<-lm(cre$avg_exp_ln~cre$Income_log) > summary(lm2) Call: lm(formula = cre$avg_exp_ln ~ cre$Income_log) Residuals: Min 1Q Median 3Q Max -1.16234 -0.20937 -0.01781 0.27643 0.55853 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 5.0611 0.2217 22.833 < 2e-16 *** cre$Income_log 0.8932 0.1126 7.929 2.95e-11 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.3457 on 68 degrees of freedom Multiple R-squared: 0.4804, Adjusted R-squared: 0.4728 F-statistic: 62.87 on 1 and 68 DF, p-value: 2.95e-11 > cre$pred2<-predict(lm2) > cre$res2<-resid(lm2) > plot(cre$res2~cre$pred2)
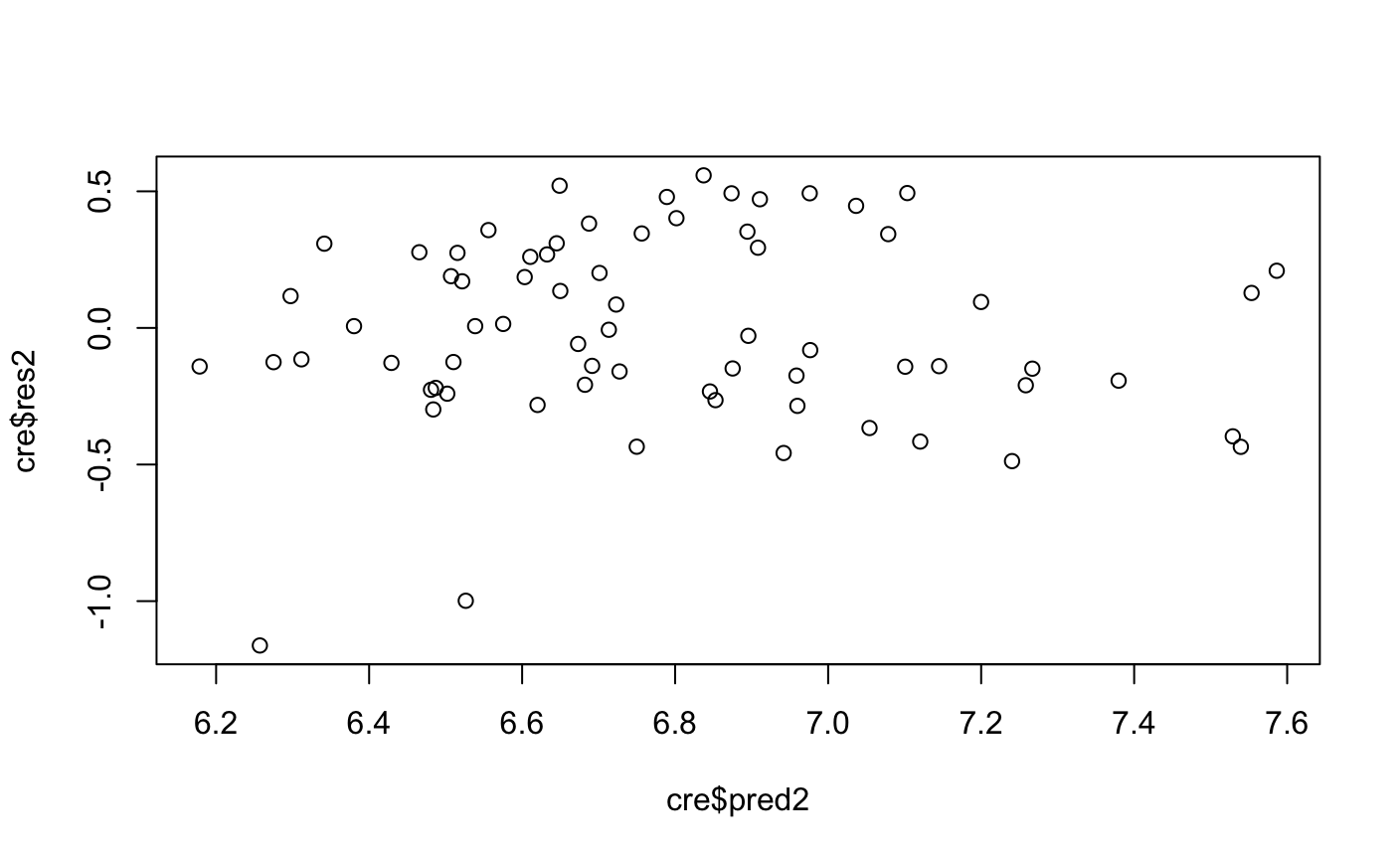
看结果已经完全消除了异方差现象,但有人会疑问,lnx和lny不是线性关系,其实x和y都是到手的数据,我们可以随意的变化。
消除强影响点
> #学生化残差消除强影响点 > cre$res_t<-(cre$res2-mean(cre$res2))/sd(cre$res2) > #选出95%的值 > cre1<-subset(cre,abs(res_t)<=2) > lm3<-lm(cre1$avg_exp_ln~cre1$Income_log) > summary(lm3) Call: lm(formula = cre1$avg_exp_ln ~ cre1$Income_log) Residuals: Min 1Q Median 3Q Max -0.47280 -0.23028 -0.05378 0.22875 0.53152 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 5.31234 0.19249 27.598 < 2e-16 *** cre1$Income_log 0.78040 0.09723 8.027 2.37e-11 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.2911 on 66 degrees of freedom Multiple R-squared: 0.494, Adjusted R-squared: 0.4863 F-statistic: 64.43 on 1 and 66 DF, p-value: 2.372e-11 > cre1$pred<-predict(lm3) > cre1$res<-resid(lm3) > plot(cre1$res~cre1$pred)
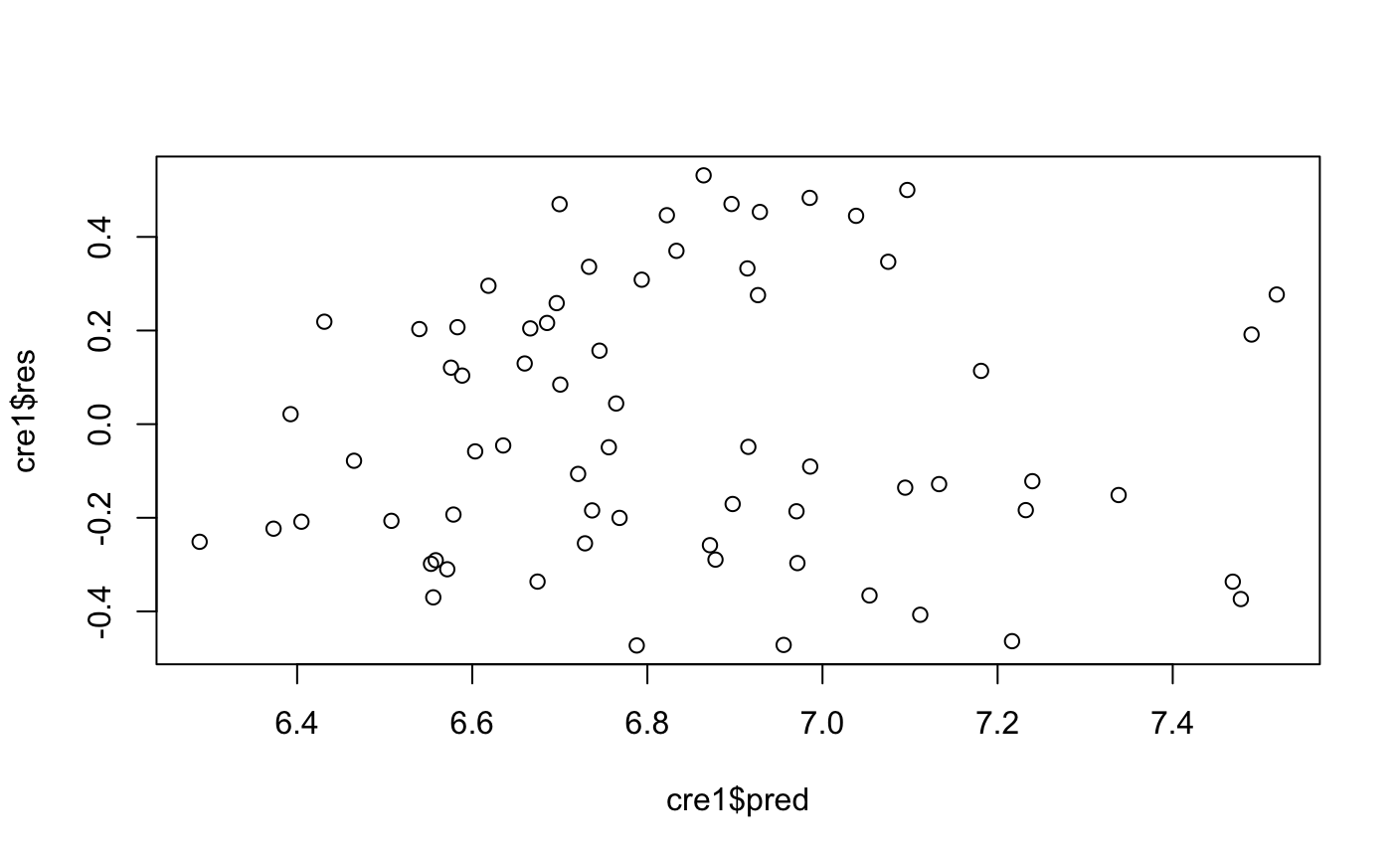
多重共线性的检测
> ###多重共线性的检测 > lm4<-lm(avg_exp~Age+Income+dist_avg_income+dist_home_val) > lm5<-step(lm4,direction = "both") Start: AIC=808.53 avg_exp ~ Age + Income + dist_avg_income + dist_home_val Df Sum of Sq RSS AIC - Age 1 5810 6306104 806.60 <none> 6300294 808.53 - dist_home_val 1 203889 6504183 808.76 - Income 1 351031 6651325 810.33 - dist_avg_income 1 862197 7162491 815.51 Step: AIC=806.6 avg_exp ~ Income + dist_avg_income + dist_home_val Df Sum of Sq RSS AIC <none> 6306104 806.60 - dist_home_val 1 205826 6511930 806.85 - Income 1 345396 6651501 808.33 + Age 1 5810 6300294 808.53 - dist_avg_income 1 857139 7163244 813.52 > library(car) > vif(lm5)#膨胀因子大于10时共线性问题就比较严重 Income dist_avg_income dist_home_val 51.176222 51.610836 1.084867
可以看出共线性的问题还是比较严重的,后续我会尝试用变量聚类,因子分析或者正则化方法消除共线性问题。