通過這一體說說三分的做法。
题目列表 > 集会
时间限制: 2000ms 内存限制: 256MB
描述
在一条河的一侧,分布着 N 个村庄。这些村庄平日里需要一些贸易往来,然而商人们来回走遍每一座村庄是非常辛苦的,于是他们决定每个月都在河边举行一次集会,大家都来集会上购买需要的物品。然而在集会地点的选择上,大家却有分歧,因为谁都不愿意集会的地点离自己村庄非常远。经过一番激烈的讨论之后,大家决定要将集会地点挑选在这样一个位置:它离最远的村庄的距离要尽可能的近。
我们把河看做一条足够长的直线,河岸就是平面坐标系上 y = 0 的这条线,y < 0 的区域是河水,而所有村庄都在 y ≥ 0 的区域里。现在给出所有村庄的平面坐标,你要在河岸上找到这样一个位置,使得它到所有村庄的最远距离最小。
输入
输入文件包含多组测试数据。
第一行,给出一个整数 T,为数据组数。接下来依次给出每组测试数据。
每组数据的第一行是一个整数 N,表示村庄的数量。接下来 N 行,每行有两个实数 xi 和 yi,表示每一个村庄的坐标。
输出
对于每组测试数据,输出一行"Case #X: Y",其中 X 表示测试数据编号,Y 表示集会地点的 x 坐标值,要求与正确答案的绝对误差在10-6以内。所有数据按读入顺序从 1 开始编号。
数据范围
小数据:T ≤ 100, 0 < N ≤ 50, 0 ≤ |xi|, yi ≤ 10000
大数据:T ≤ 10, 0 < N ≤ 50000, 0 ≤ |xi|, yi ≤ 10000
- 样例输入
-
1 5 0 8 1 6 4 4 -5 7 -6 1
- 样例输出
-
Case #1: -1.000000
題外話:
假設函數f(x) =a*x^2+b*x+c
a = 0,b!=0時退化為一條直線,這個時候滿足單調性,我們可以通過二分來做。
當a!=0時,他為一條抛物線,這個時候我們可以用三分來做。
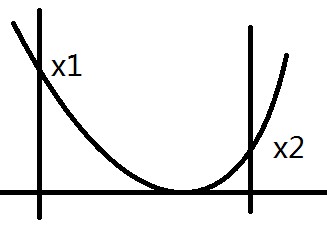
分析:
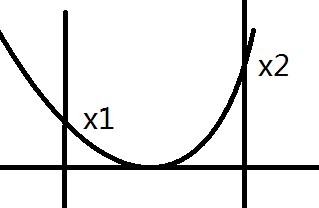
如上圖。
假設最優點為x,往x的左面走到x1,距離會增大,往x的右面走到x2,距離同樣會增大。
由於只有一個極值點,我們假設區間為[l,r]。
1.找出兩個點x1,x2(上圖不是很准確。。。),這兩個點剛好把[l,r]分成相等的三個部份。
2.判斷f(x1)與f(x2)哪個更優。
如果f(x1)>f(x2),如左圖,則把l = x1
否則,r = x2
3.重複1,2,直到滿足精度。
由於精度不好控制,我們可以直接設置調整的步數,從題目數據我們可以估計出步數的範圍可以假設為100,(2/3)^100次方肯定能夠滿足精度要求了。。。
代碼如下:
#include <set>
#include <map>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define lx(x) (x<<1)
#define rx(x) (x<<1|1)
#define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
/******** program ********************/
const int MAXN = 50005;
struct node{
double x,y;
}p[MAXN];
int n;
double dis(double x,double y){
return x*x+y*y;
}
double cal(double now){
double tmp = 0;
rep(i,n)
tmp = max( tmp,dis(p[i].x-now,p[i].y) );
return tmp;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif
int ncase;
RD(ncase);
rep1(Ncase,ncase){
printf("Case #%d: ",Ncase);
RD(n);
double L = 10000,R = -10000;
rep(i,n){
scanf("%lf%lf",&p[i].x,&p[i].y);
L = min(L,p[i].x);
R = max(R,p[i].x);
}
double l = 0,r = 1;
double px1,px2;
rep(step,100){
double m1 = (2*l+r)/3;
double m2 = (l+2*r)/3;
px1 = L*(1-m1)+R*m1;
px2 = L*(1-m2)+R*m2;
double tmp = cal(px1);
double ret = cal(px2);
if(tmp>ret)
l = m1;
else
r = m2;
}
if(px1<0&&fabs(px1)<1e-9) // 判斷是否會出現-0.000000
px1 *= -1.0;
printf("%.6lf\n",px1);
}
return 0;
}
大家有空可以做做CF 8D這題,很經典的三分套三分做法。。。
以上~~