- 平衡二叉查找树
AVL树的实现中,需要对每个节点跟踪 “平衡因子balance factor”参数
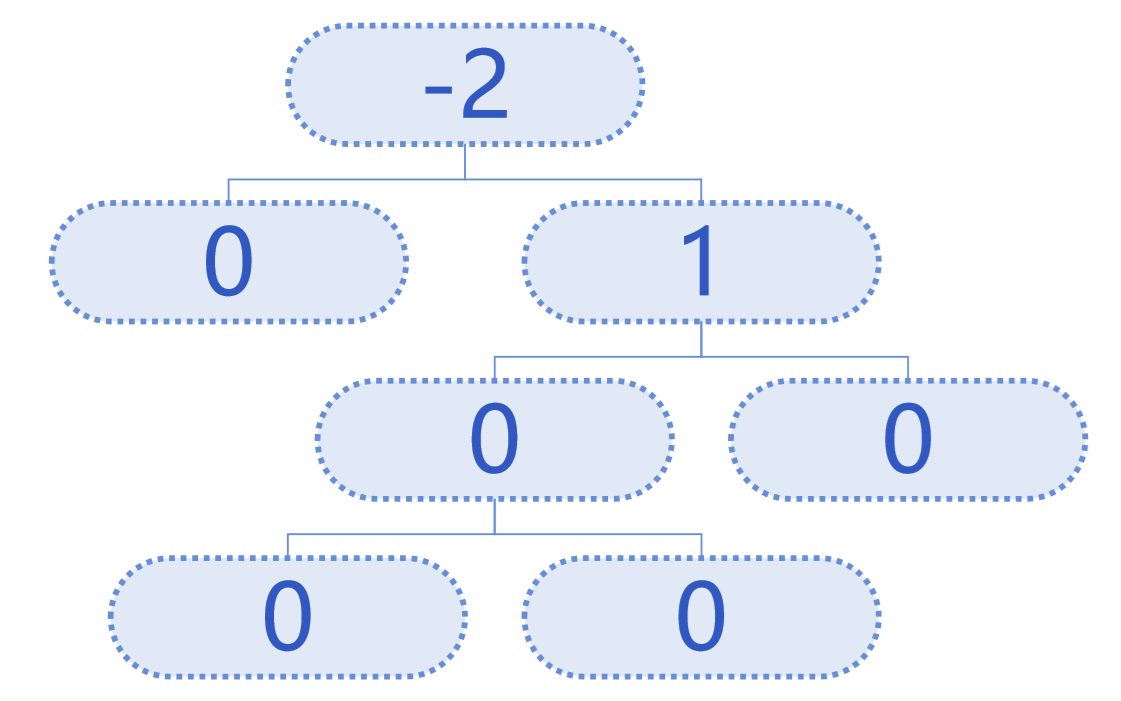
平衡因子是根据节点的左右子树的高度来 定义的,确切地说,是左右子树高度差:

如果一个二叉查找树中每个节点的平衡因 子都在-1,0,1之间,则把这个二叉搜索 树称为平衡树 :
- AVL树性能分析
我们来分析AVL树最差情形下的性能:即 平衡因子为1或者-1 下图列出平衡因子为1的“左重”AVL树,树的高 度从1开始,来看看问题规模(总节点数N)和比 对次数(树的高度h)之间的关系如何?
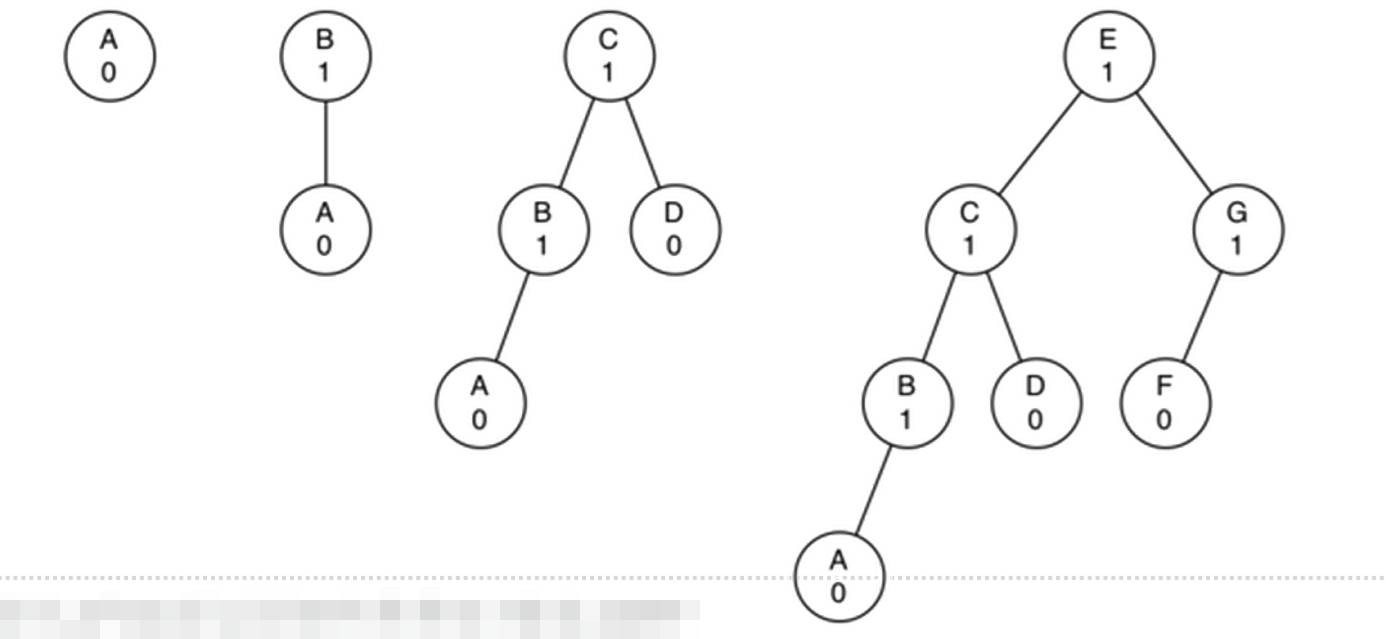
观察上图h=1~4时,总节点数N的变化
h= 1, N= 1
h= 2, N= 2= 1+ 1
h= 3, N= 4= 1+ 1+ 2
h= 4, N= 7= 1+ 2+ 4
![]()
反正最后就是推出了AVL树的搜索时间复杂度为O(log n)
- AVL树的python实现
这里首先有个重要的性质需要记住:向AVL加入一个新key,则有这样的情况存在:
叶子节点:叶节点的平衡因子是0,其本身无需重新 平衡
父节点:作为左子节点插入,则父节点平衡因子会增加1; 作为右子节点插入,则父节点平衡因子会减少1。
这种影响可能随着其父节点到根节点的路 径一直传递上去,直到传递到根节点为止; 或者某个父节点平衡因子被调整到0,不再影响上层节点的平衡因子为止。
然后代码比较复杂,这里也不赘述了。。。。
这两节博客都比较水。