【算法导论】第1、2章，算法入门

【1】算法简介

1.1 

排序的重要问题：

1、排序项数

2、已经排序的程度、

3、项值的可能限制

4、计算机体系结构

5、储存设备的种类

1.2 

衡量算法的主要标准：时间 & 空间

【2】算法入门

2.1 插入排序

循环不变式：前i个总是排好顺序的。增量法

插入排序python代码

def insertSorted(xList):
    n = len(xList)
    for sortIdx in range(1, n):
        cache = xList[sortIdx]
        idx = sortIdx - 1
        while idx >= 0 and xList[idx] > cache:
            xList[idx+1] = xList[idx]
            idx -= 1
        xList[idx+1] = cache
    return xList

if __name__ == '__main__':
    print insertSorted([1, ])
    print insertSorted([2, 1])
    print insertSorted([2, 2, 1])
    print insertSorted([2, 3, 4, 1])
    print insertSorted([1, 2, 4, 3])
    randomList = range(10)
    random.shuffle(randomList)
    print 'random:', randomList
    print insertSorted(randomList)

2.2 算法简单分析

在分析算法之前，要建立实现技术的模型：单处理器，随机存取机（RAM）： 无法并行，不包含层次存储。

算法的有效性：通常是时间

常见的常数时间指令：算术指令（加减乘除、取余、向上下取整），数据移动指令（装入、储存、复制），控制指令（转移，子程序调用与返回），2^k

插入排序的平均情况O(n^2), 

2.3 另外的算法设计方法

分治法：递归解决问题

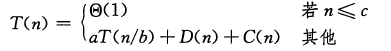
D(n)为分解问题需要的时间

C(n)是子问题合成为原问题的时间

对于本问题，每一层代价都是cn，总共有lg(n)层

合并排序Python代码

def merge(originList, start, mid, end):
    xList = originList[start:mid] + [np.inf]
    yList = originList[mid:end] + [np.inf]
    zList = []
    idxX, idxY = 0, 0
    for i in range(len(xList + yList) - 2):
        x, y = xList[idxX], yList[idxY]
        if x < y:
            zList.append(x)
            idxX += 1
        else:
            zList.append(y)
            idxY += 1
    originList[start:end] = zList
    return originList

def mergeSort(xList, start=0, end=None):
    if end is None:
        end = len(xList)
    if start < end - 1:
        mid = int((start + end) / 2.)
        mergeSort(xList, start, mid)
        mergeSort(xList, mid, end)
        xList = merge(xList, start, mid, end)
    return xList


if __name__ == '__main__':
    print mergeSort([1, ])
    print mergeSort([2, 1])
    print mergeSort([2, 2, 1])
    print mergeSort([2, 3, 4, 1])
    print mergeSort([1, 2, 4, 3])
    randomList = range(10)
    random.shuffle(randomList)
    print 'random:', randomList
    print mergeSort(randomList)