今天学习B树和B+树,B树和B+树都是基于二叉树的衍生,对于二叉树不太了解的读者可以翻看《数据结构:二叉树》
本文目录:
B树
定义及特性
B树,在写法上通常是B-树,这不是减号的意思,只是一种表达方式,它是一种能够存储数据、对数据进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。,概括来说是一个节点可以拥有多于2个节点的二叉查找树。
一个m阶的B树具有如下特点:
-
B树根节点至少有两个节点,每个节点可以有多个子树;
-
每个中间节点都包含k-1个元素和k个子树,其中 m/2 <= k <= m ;
-
所有的叶子结点都位于同一层;
-
每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
看概念还是挺晦涩的,直接放张图看看正宗的B树
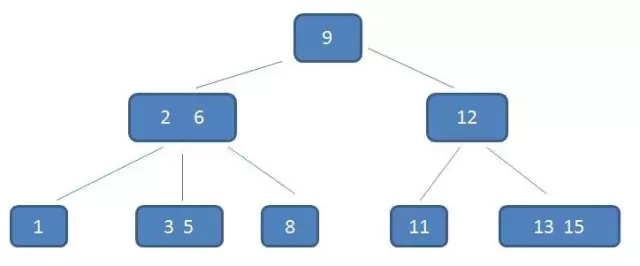
可以看出,B树的节点可以有多个数据,并且可以拥有不只两个子树,左边子树的数据都比节点的数据小,右边子树的数据都比节点的数据大。
比起正常的平衡二叉树,B树每个节点显然能存储的数据更多,在查找数据方面也显得比较高效,所以B树被广泛应用于磁盘IO读取较为频繁的系统中。
查找顺序
在B树中,一般的查找顺序如下:
-
从根节点开始,如果查找的数据比根节点小,就去左子树找,否则去右子树
-
和子树的多个关键字进行比较,找到它所处的范围,然后去范围对应的子树中继续查找
-
以此循环,直到找到或者到叶子节点还没找到为止
保持平衡
B树查找的高效性是基于其独特的结构,一旦有数据插入或者删除,那么B树就需要调整自身来保持平衡。B树的平衡特性有三点:
-
叶子节点都在同一层
-
每个节点的关键字数 (也就是数据个数) 为子树个数减一(子树个数 k 介于 m/2 <= k <= m
-
子树的数据保证左小右大的顺序
举例子说,一棵4阶的B树,节点最多有4个子树,每个节点的关键字数最少为1,最多为3,插入数据时,如果要插入的子树的关键字数已经是最多,就需要拆分节点,调整B树的结构。
下面是一张从网上找到的动态图,完整展示了4阶B树的插入并调整结构的过程。
插入的数据依次是:6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4,效果图如下:

我比较懒,所以具体的插入过程就不做一一分析了,图片插入过程也比较清晰,读者自己可以慢慢研究。
B+树
说完B树,再来说说B+树,B+树和结构很类似,但查询性能上更高,具有如下的特性:
-
有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点;
-
叶子节点中包含了全部元素的信息,按照关键字的大小从左到右排序;
-
中间节点的元素同时存在于子节点中,在子节点元素中是最大。
下面放张示例图:
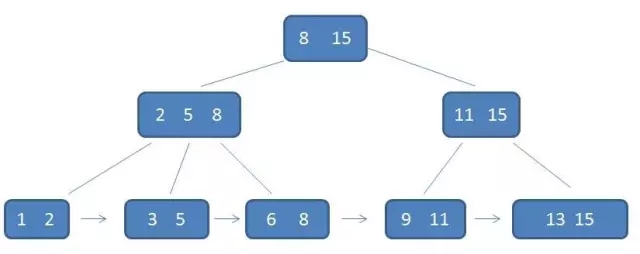
从图中可以看出,B+树中间节点和叶子节点有重复的数据,这里声明一下,中间节点保存的只是子树数据的子针,并不是真实的数据,所以中间节点的存储占用空间较少。
同时,叶子节点之间用指针连在一起,换句话说,叶子节点形成了一个链表,把所有的数据都存储了进来。
为什么这样设计,比起B树有什么好处呢?
首先,因为B+树的中间节点只是保存子树的最大数据和子树的子针,本身的占用空间较小,因此可以容纳更多节点元素,也就是说同样数据情况下,B+ 树会 B 树更加“矮胖”,因此查询效率更快。
其次,查找某个范围的数据,只需在B+树的叶子节点链表中遍历即可,不需要像B 树那样挨个中序遍历比较大小。总结来说,B+树的优点就是:
-
层级更低,IO 次数更少;
-
每次都需要查询到叶子节点;
-
查询性能稳定叶子节点形成有序链表,范围查询方便
B+树的插入
B+树的插入过程也是比较麻烦的,因为也需要保持平衡,这里也是给大家展示一张动态图,具体就不分析了。

使用场景
最后说一下B树和B+树的使用场景,通过前面的学习,我们了解了这两种树都是可以有效减少IO次数的数据结构,基于这个优点,它们被广泛应用于磁盘文件系统中,
例如 windows的HPFS 文件系统、Linux的文件系统、Mysql的索引等,尤其是Mysql的索引结构,这是面试中的常见问题,所以,了解B树和B+树还是非常有必要的。