【算法导论】归并排序

1. 分治法：分治模型在每层递归的时都有三个步骤：

　　a.分解原问题为若干个子问题，这些子问题是原问题的规模较小的实例；

　　b. 解决这些子问题，递归地求解各子问题的规模足够小，则直接求解；

　　c. 合并这些子问题的解 成 原问题的解。

2. 归并排序算法完全遵循分治模式。

　　a. 分解：分解待排序的n个元素的序列成各具 n/2 个元素的子序列

　　b. 解决：使用归并排序递归地排序子序列

　　c. 合并：合并两个已经排序的子序列以产生已排序的答案。

3.归并排序算法图示，实话说我没看懂第一个图。。但是第二个图很好理解

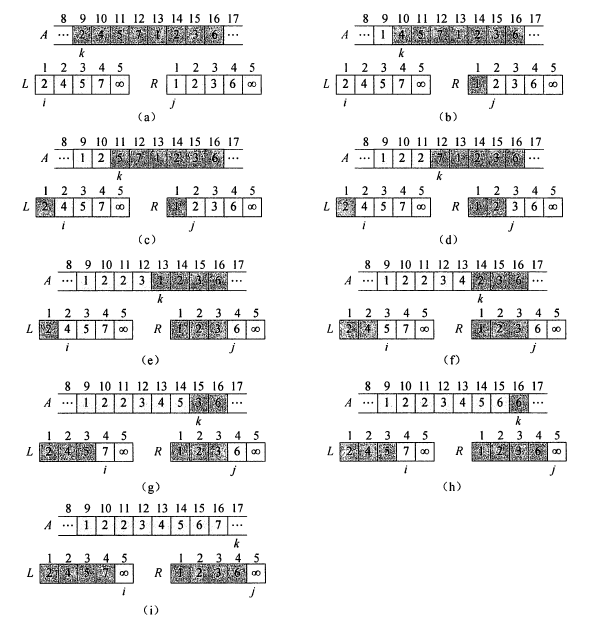
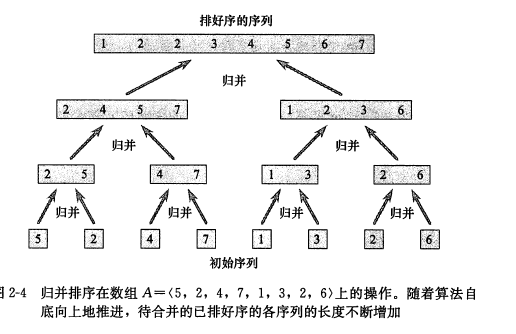
4. 伪代码

MERGE(A, p, q, r)
    n1 = q-p+1
    n2 = r-q
    //let L[1....n1+1] and R[1....n2+1] be new arrays
    for i =1 to n1
         L[i] = A[p+i-1]
    for j=1 to n2
        R[j] = A[q+j]
    L[n1+1] = ∞
    L[n2+1] = ∞
    i=1
    j=1
    for k =p to r
        if L[i]<=R[j]
            A[k] = L[i]
            i = i + 1
        else
            A[k]=R[j]
            j = j+1

MERGE-SORT(A,p,r)
    if p < r
        q =(p+r)/2  //向下取整，不会打那个符号
        MERGE-SORT(A, p, q)
        MERGE-SORT(A, q+1, r)
        MERGE(A, p, q, r)

 5. 算法分析：

　　排序就是比较，比较最终都是两个数比较

　　直接看MERGE（A, p, q, r）这个算法,这个算法的前提就是假设 A[p] - A[q]是有序的， A[q+1]到A[r]是有序的，那么归并后肯定是有序的.

　　怎么做到这个前提，就是最终把所有的数分到最小粒度， 也就是数组只有一个数的时候，它一定是有序的， 然后一层一层向上归并，得到最终的有序序列

6. 代码实现

　　java　　

void mergeSort(int[] A, int p, int r) {
    if (p < r) {
        int q = (int)Math.floor((p + r)/2);
        mergeSort(A, p, q);
        mergeSort(A, q+1, r);
        merge(A, p, q, r);

    }
}

void merge(int[] A, int p, int q, int r){
    int n1 = q - p + 1;
    int n2 = r - q ;
    int[] L = new int[n1 + 1];
    int[] R = new int[n2 + 1];
    for (int i = 0; i < n1; i++) {
        L[i] = A[p+i];
    }
    for (int j = 0; j < n2; j++) {
        R[j] = A[q+j+1];
    }
    L[n1] = R[n2] = Integer.MAX_VALUE;
    int i = 0, j = 0;

    for (int k = 0; k < r - p + 1; k++) {
        if (L[i] <= R[j]) {
            A[p+k] = L[i];
            i++;
        } else {
            A[p+k] = R[j];
            j++;
        }
    }
}

python

import math
import sys


def merge_sort(arr, p, r):
    if p < r:
        q = math.floor((p + r) / 2)
        merge_sort(arr, p, q)
        merge_sort(arr, q + 1, r)
        merge(arr, p, q, r)


             # 0, 5, 10
def merge(arr, p, q, r):
    n1 = q - p + 1
    n2 = r - q
    m = []
    n = []
    for i in range(n1):
        m.append(arr[p+i])
    for j in range(n2):
        n.append(arr[q+j+1])
    m.append(sys.maxsize)
    n.append(sys.maxsize)
    i = j = 0
    for k in range(r - p + 1):
        if m[i] <= n[j]:
            arr[p+k] = m[i]
            i += 1
        else:
            arr[p+k] = n[j]
            j += 1

c语言

 //                            0,     10
void merge_sort(int arr[], int p, int r)
{
    if(r > p)
    {
        int q = (p + r) / 2;
        merge_sort(arr, p, q);
        merge_sort(arr, q + 1, r);
        merge(arr, p, q, r);
    }
}
 //                        0,     5,     10
void merge(int arr[], int p, int q, int r)
{
    int n1 = q - p +1;
    int n2 = r - q;
    int L[n1+1], R[n2+1];
    int i, j, k;
    for(i = 0; i < n1; i++)    
        L[i] = arr[p+i]; 
    
    for(j = 0; j < n2; j++)
        R[j] = arr[q+j+1];
    L[n1] = R[n2] = (unsigned)(~0) >> 1;
    i = j =0;
    for(k = 0; k < r - p +1; k++)
    {
        if(L[i] <= R[j])
        {
            arr[p+k] = L[i];
            i++;
        }
        else
        {
            arr[p+k] = R[j];
            j++;
        }
    }
}