由这个想到的;https://www.cnblogs.com/nullllun/p/8350178.html
31乘以某个数能不能写成这个数乘以2的次幂 再减去这个数。
用数学语言表达一下就是:
设这个数为x
31*x=x*2^n-x
这个等式是否存在,如果存在,求n的值
那我们计算一下,
31=2^n -1
得2^n=32
得n=5
也就是说存在那么一个n使得,31乘以某个数的结果等于这个数乘以2的n次幂再减去一个数。
所以,一个乘法运算,最后就转化成了一个速度较快的移位运算了。
我们再试试另外的数
63*i=i*2^n-i这个等式是寸存在,若存在,求出n的值。
最后得出n=6
有没有发现规律,31等于2的n次方-1,63也等于2的n次方-1
所以一个(2^n-1)乘以某个数的结果可以被优化为这个数乘以2的n次方再减去这个数。
然后我又做了几个实验。
因为9=2^4+1;
然后自然就想到了9乘以某个数是否能写成这个数乘以2的n次幂,再加上这个数
9*i=i*2^n+i是否成立,如果成立,求n
n=4,也就是说9乘以某个数是等于这个数乘以2的n次幂再加上这个数的。
事实上,编译器也是这么优化的。
我写了一段代码,用来计算9和任意一个整数的乘法。
int x =9;
int input = 0;
scanf_s("%d",&input);
printf("%d",9*input);
用IDA查看一下关键代码,9是怎么被优化的。
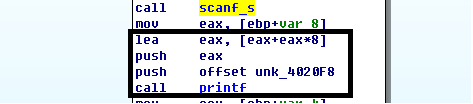
有一点必须直到,eax是作为printf的参数,printf的输出结果就是eax的值,这需要一点汇编知识。
那我们看lea中eax是怎么计算的。
用数学语言翻译过来是不是就是这样:
9*eax=eax*8 + eax;把eax换成i
9*i=i*2^n+i
和前面是相符的。
经过测试发现如果是单变量乘以某个常数这种情况的话,优化策略是这样的:
如果这个常数可以被写成2^n,(2^n)+1,(2^n)-1,2^n(1+2^m) 这几种情况的话,那么就被优化了。
2^n(2^m-1) 这种情况并不优化,直接用的是imul指令