引言
本文主要适用于自我学习复习和理解使用。(能给我点个赞更好了TuT)
参考
FROM
- OI-WIKI
- 水群
简介
Blossom Algorithm (带花树算法)主要用于解决一般图最大匹配问题
从二分图匹配到一般图匹配
Q:一般图匹配和二分图匹配问题的差别是在于哪里呢?
A:一般图可能存在奇环。
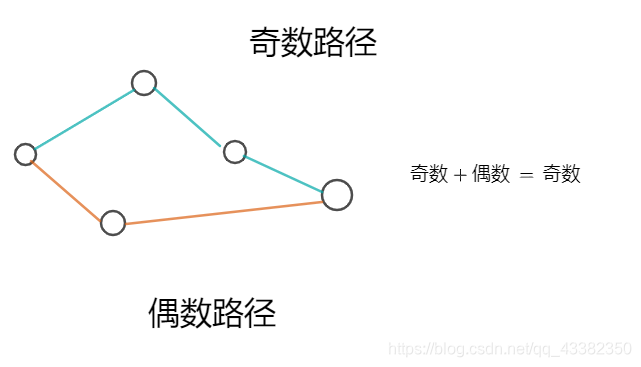
解释,奇环:即从A点到B点存在一条偶数长度的路径,也存在一条奇数长度的路径,两条路径结合构成一个和为奇数的路径也是环
我们可以通过二分图染色问题去考虑,
在二分图染色问题中奇路径的两个点的颜色一定不同,偶路径的两个点的颜色一定相同。
那如果存在奇环呢?
显然不行呀!最右点:我是什么颜色???
综上,我一般图匹配不能跟你二分图匹配一般见识,所以也就不能直接通过增广路寻找惹。
那好,我们不如直接假设接下来我们解决的图中是存在奇环的。
奇环就像上图所示,但点数可能会比上图的多,故
我们不妨设
某图中的某奇环点数为 (奇数)
那我们就要对奇环部分特殊处理了,点数为 很明显能够成功匹配的点有个,还会剩下1个点无法匹配,这个点所谓的无法匹配也仅仅是无法在这个奇环内进行匹配,但是它却可以拥有向外连边进行匹配的权利。
- 下面考虑一般图的增广算法。
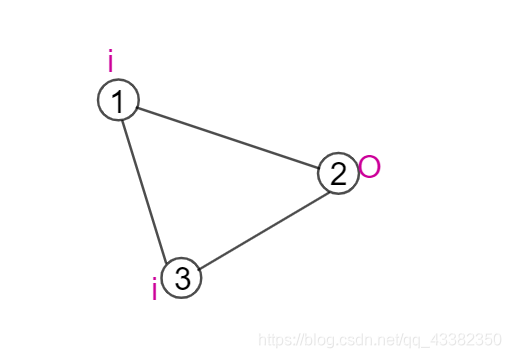
从二分图的角度出发,每次枚举一个未匹配点(也就是上面 中的 ),搜索开始先设出发点为根并压入队列中,标记为 “o” ,接下来交错标记 “o” 和 “i” ,不难发现 “i” 到 “o” 这段边是匹配边。
(拿个无敌小的图帮助下理解,是不是如上面所说一致)
- 假设当前点是 ,相邻点为 。
case 1: 未拜访过,当 是未匹配点,则找到增广路径,否则从 的配偶找增广路。
case 2: 已拜访过,遇到标记 “o” 代表需要 缩花 ,否则代表遇到偶环,跳过。
遇到偶环的情况,将他视为二分图解决,故可忽略。 缩花 后,再新图中继续找增广路。
(还是可以通过上图进行理解)(如果不太好理解的话可以去看看见OI-wiki的图)
算法复杂度

例题
链接
题意
警卫不敢一个人独自看守,于是计划成对看守

每行输入 表示 警卫可以和 警卫是可以一起进行工作的,寻找最佳匹配,为这些可以一起看守的警卫每一对提供一种制服,问需要多少种,匹配情况是什么样的。
题解
一般图最大匹配,看守我肯定是希望对数阅读越好,那样能看守的人肯定是最多的,所以就是最大匹配。
样例
输入
3
1 2
2 3
1 3
输出
2
1 2
需要制服的件数(注意哦一对是两件),匹配成功的情况是(1,2)

代码
const int MAXN = 250;
int N; // 点的个数
bool Graph[MAXN][MAXN]; //图
bool InQueue[MAXN],InPath[MAXN], InBlossom[MAXN]; //判断是否在队列内、是否访问过、是否开花过
int Start, Finish; //起始、结束
int Head, Tail;
int NewBase;
int Match[MAXN]; //匹配
int Father[MAXN], Base[MAXN]; //用于lca的处理
int Count = 0; //匹配成功的数量
int Queue[MAXN]; //模拟队列,也可以直接用stl库内的queue直接进行实现
void CreateGraph(){
int u, v; RST(Graph); //对图进行初始化
RD(N); // 输入顶点个数
//没有给出输入边的要求,就采用循环输入,直到输入文件结束
while(scanf("%d%d", &u, &v) == 2){
Graph[u][v] = Graph[v][u] = true; //u到v两点之间的双向边存在
}
}
//队列的实现 弹出
/*
* push 压入队列
* Pop 从队列内
*/
void Push(int u){
Queue[Tail] = u;
Tail++;
InQueue[u] = true; //表示u点已经进入队列
}
int Pop(){
int res = Queue[Head];
Head++;
return res;
}
//寻找第一个匹配的顶点
int FindCommonAncestor(int u, int v){
RST(InPath); //初始化是否访问过路,全部初始化为false,表示没有访问过
while(true){
u = Base[u];
InPath[u] = true;
if(u == Start) break;
u = Father[Match[u]];
}
while(true){
v = Base[v];
if (InPath[v]) break; //如果v这个点的path是访问过的就可以直接跳出
v = Father[Match[v]]; //lca寻找公共祖先,与v匹配的点的最近公共祖先 father[match[v]]
}
return v;
}
//回跳
void ResetTrace(int u){
int v;
while(Base[u] != NewBase){
v = Match[u];
InBlossom[Base[u]] = InBlossom[Base[v]] = true;
u = Father[v];
if (Base[u] != NewBase) Father[u] = v;
}
}
void BloosomContract(int u, int v){
NewBase = FindCommonAncestor(u, v);
memset(InBlossom, false, sizeof(InBlossom));
ResetTrace(u);
ResetTrace(v);
if (Base[u] != NewBase) Father[u] = v;
if (Base[v] != NewBase) Father[v] = u;
for(int tu = 1; tu <= N; tu++){
if (InBlossom[Base[tu]]){
Base[tu] = NewBase;
if (!InQueue[tu]) Push(tu);
}
}
}
//寻找增广路径
void FindAugmentingPath(){
RST(InQueue);
RST(Father);
for(int i = 1; i <= N; i++){
Base[i] = i;
}
Head = Tail = 1;
Push(Start);
Finish = 0;
while(Head < Tail){
int u = Pop();
for(int v = 1; v <= N; v++){
if (Graph[u][v] && (Base[u] != Base[v]) && (Match[u] != v)){
if ((v == Start) || (Match[v] > 0 && Father[Match[v]] > 0)) BloosomContract(u, v);
else if (Father[v] == 0){
Father[v] = u;
if (Match[v] > 0) Push(Match[v]);
else {
Finish = v;
return ;
}
}
}
}
}
}
void AugmentPath()
{
int u,v,w;
u = Finish;
while(u > 0)
{
v = Father[u];
w = Match[v];
Match[v] = u;
Match[u] = v;
u = w;
}
}
void Edmonds()
{
memset(Match,0,sizeof(Match));
for(int u = 1; u <= N; u++)
if(Match[u] == 0)
{
Start = u;
FindAugmentingPath();
if(Finish > 0) AugmentPath();
}
}
//输出匹配结果
void PrintMatch()
{
Count = 0;
for(int u = 1; u <= N;u++)
if(Match[u] > 0)
Count++;
OT(Count);
for(int u = 1; u <= N; u++)
if(u < Match[u])
printf("%d %d
",u, Match[u]);
}
int main(){
//cout << false << 0 << '
';
CreateGraph();//建图
Edmonds();//Edmonds' algorithm 匹配
PrintMatch();
}
综上
以上内容是一次性书写的,很多地方没有经过太仔细的考虑所以可能存在许多纰漏,会逐步进行完善和丰富的。